使用R语言对两种结核病发病预测模型的对比分析
汪 洋,胡代玉,杨德香,刘 瑛,王润华,易 静
2000年全国结核病流行病学调查显示,我国目前约有5.5亿人感染了结核分枝杆菌,我国现有活动性肺结核病患者约450万人,每年新增结核病患者约150万人,每年死于结核病的患者约有25万,仍为各类传染病之首[1]。根据结核病变化规律建立结核病疫情发展预测模型,逼近准确的结核发病率,可以量化对结核的控制和管理的决策,是有效的结核病防治工作的前提。本研究采用免费开源的R语言中的神经网络分析模型和灰色模型进行结核病发病情况的分析与预测,现报道如下。
1 资料与方法
1.1 一般资料 资料来源于重庆市结核病防治所1993—2009年的结核病发病登记数据。
1.2 研究方法
1.2.1 R语言程序 R是由AT&T贝尔实验室所创的s语言发展出的有着统计分析及强大作图功能的软件系统。R语言内含的作图函数能将产生的图片展示在一个独立的窗口中,并能将之保存为各种形式的文件(jpg、png、bmp、ps、pdf、emf、pictex、xfig,具体形式取决于操作系统)。统计分析的结果也能直接显示出来,一些中间结果(如P值、回归系数、残差等)既可保存到专门的文件中,也可以直接用作进一步的分析[2]。与SPSS、MATLAB等相比,R作为一个开源的免费软件,其价值得到不断的延伸,主要表现在:可以跨平台运行,对矩阵的操作强大而高速,拥有许多可用的附加包,灵活的编程环境,对于已经广泛使用的统计软件是可兼容的[3]。
1.2.2 BP神经网络的建模过程 BP神经网络通常有一个或多个sigmoid隐层和线性输出层,能够对具有有限个不连续点的函数进行逼近[4]。其学习过程由两部分组成:正向传播与反向传播。正向传播让输入信息在相应权值、阈值和激活函数的作用下传递到输出层,当输出的结果和期望值的误差大于给定精度时,则将误差反向传播。在误差返回过程中,网络修正各层的权值和阈值。如此反复迭代,最后使传递信号的误差达到允许精度。模型的设计包括:网络类型及层数的确定;输入及输出变量的选择;隐含层神经元数目的确定;激活函数的选择。常用的三层BP神经网络模型结构见图1。

图1 三层BP网络结构
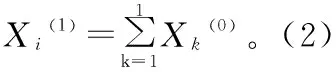
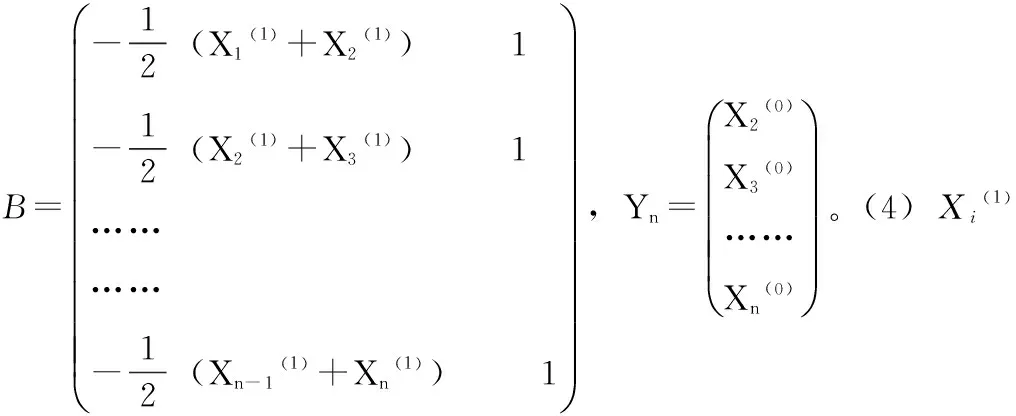
2 结果
2.1 结核病发病登记数据 重庆市结核病防治所1993—2009年的结核病发病登记数据见表1。

表1 重庆市1993—2009年的结核病发病登记数据(含涂阴、涂阳病例)
2.2 神经网络模型
2.2.1 数据准备 使用重庆市结核病防治所1993—2009年的结核病发病登记数据,将1993—2007年的登记数据作为建模数据,2008—2009年的登记数据用于验证预测的准确性。按照此次神经网络训练的模式设计,输入层有3个结点,隐含层结点数为3,隐含层的激活函数为tansig;输出层结点数为1个,输出层的激活函数为logsig,设置学习速率为0.05,收敛误差界值为0.005。
依据下列公式对原始数据进行初始化。
Pmax=max〔P〕
Tmax=max〔T〕
Pmn=P/Pmax
Tmn=T/Tmax
集合变量P为1993—2007年结核病登记发病数,Pmax为集合中的最大值,同样,T为输出量集合,Tmax为输出量集合中的最大值,Pmn和Tmn为集合P、T经过归一化处理后的实验数据,代码如下:P=c(8135,10329,11174,12264,15781,14387,15674,16402,18018,17187,23505,28836,29644,28349,29119);#1993—2007年发病数,赋值给P
Pmn=c();#归一化数据存储变量
Pmax=max(P);#取最大值
len=length(P);#计算长度
for(i in 1:len){
Pmn[i]= P[i]/Pmax;
〕 #循环处理每一个归一化元素
Pdata=matrix(nrow=12,ncol=3) #创建12*3的矩阵用于存储训练数据的输入集,以1993、1994、1995年的归一化数据为一组,1994、1995、1996年的归一化数据为一组,以此类推共12组数据。
k=1;
for(i in 1:12){
for(j in 1:3) {
Pdata[i,j]=Pmn[k];
k= k+1;
}
k=k-2;
}
T=c(12264,15781,14387,15674,16402,18018,17187,23505,28836,29644,28349,29119);#输出集,为1996—2007年结核病登记病例数归一化值。
Tmax=max(T);
Tdata=c();
len=length (T);
for(i in 1:len) {
Tdata[i]=T[i] / Tmax;
}
2.2.2 建模与预测结果 有超过1 800个免费的预测分析功能包供下载,地址:http://cran.r-project.org[6]。此处需要:AMORE、Rserve,下载地址:http://cran.csdb.cn/web/packages/available_packages_by_name.html。
利用R语言中的神经网络模型(AMORE)模块建立神经网络模型的代码如下:
library(AMORE); #加载神经网络算法包
net=newff(n.neurons=c(3,3,1,1),learning.rate.global=1e-2,momentum.global=0.5,
error.criterium=“LMS”,Stao=NA,hidden.layer=“tansig”,
output.layer=“purelin”,method=“ADAPTgd”);#新建一个神经网络
result=train(net,Pdata,Tdata,error.criterium="LMS",report=TRUE,show.step=100,n.shows=5);#训练结果。
P2=c(29644,28349,29119,27098,25010);#预测2008、2009年的结核病发病例数。为满足输入层有3个结点,隐含层结点数为3的条件,使用2005—2009年的结核病登记病例数作为输入集。
P2max=max(P2);
len=length(P2);
P2mn=c();
for(i in 1:len) {
P2mn[i]=P2[i]/P2max;
}
Pdata2=matrix(ncol=3,nrow=3);
k=1;
for(i in 1:3) {
for(j in 1:3) {
Pdata2[i,j]=P2mn[k];
k= k+1;
}
k= k-2;
}
y=sim(result$net,Pdata2);
预测结果如下:
[,1]
[1,] 0.8707301
[2,] 0.8506458
[3,] 0.8381221
将2008—2009年的归一化预测结果即[1,1]和[2,1]的值与Pmax相乘得到相应的预测结,见表2。
表2 神经网络模型对重庆市2008年和2009年的结核病预测结果
Table2 Forecast results of tuberculosis by neural network model in Chongqing city in 2008 and 2009

年份登记病例数Pmax归一化预测结果预测结果误差200827098296440.87073025811.920124.75%200925010296440.85064625216.550020.83%
注:2010年的实际登记病例数未获得,不能评价本模型的误差
2.3 灰色模型(GM1,1)
2.3.1 模型函数准备
R语言中暂无灰色模型,可手工实现R语言的灰色模型函数,其代码如下:
gm<-function(x0,t){
x1<-cumsum(x0)
b<-numeric(length(x0)-1)
n<-length(x0)-1
for(i in 1:n){
b[i]<--(x1[i]+x1[i+1])/2
b}
D<-numeric(length(b))
D[]<-1
B<-cbind(b,D) BT<-t(B)
M<-solve(BT%*%B)
YN<-numeric(length(x1)-1)
YN<-x0[2:length(x0)]
alpha<-M%*%BT%*%YN
alpha2<-matrix(alpha,ncol=1)
a<-alpha2[1]
u<-alpha2[2]
cat("Model parameters:",′/n′,"a=",a,"u=",u,′/n′,′/n′)
y<-numeric(length(c(1:t)))
y[1]<-x1[1]
for(w in 1:(t-1)){
y[w+1]<-(x1[1]-u/a)*exp(-a*w)+u/a
}
cat("1AGO predictions:",′/n′,y,′/n′,′/n′)
xy<-numeric(length(y))
xy[1]<-y[1]
for(o in 2:t){
xy[o]<-y[o]-y[o-1]
}
cat("The predict values:",′/n′,xy,′/n′,′/n′)
y0<-numeric(length(x0))
y0[1]<-x1[1]
for (q in 1:n){
cc<-exp(-a*q)
y0[q+1]<-(x1[1]-u/a)*cc+u/a
}
xp<-numeric(length(x0))
m<-length(x0)
xp[1]<-y0[1]
for(j in 2:m){
xp[J]<-y0[J]-y0[j-1]
}
e<-numeric(length(x0))
for (l in 1:m){
e[l]<-xp[l]-x0[l]
}
cat("Residuals:",′/n′,e,′/n′,′/n′)
se<-sd(e)
sx<-sd(x0)
cv<-se/sx
cat("Test for raw data:",′/n′,cv,′/n′,′/n′)
if(cv<0.35) cat("prediction is good",′/n′)
else cat("prediction is not good",′/n′)
plot(xy,col=′blue′,type=′b′,pch=16,xlab=′Time series′,ylab=′Values′)
points(x0,col=′red′,type=′b′,pch=18)
legend(′topright′,c(′Predictions′,′Raw data′),pch=c(16,18),lty=l,col=c(′blue′,′red′))
}
2.3.2 预测结果 调用上节创建的灰色模型函数进行结核病发病情况预测,代码如下:gmData=c(8135,10329,11174,12264,15781,14387,15674,16402,18018,17187,23505,28836,29644,28349,29119); #定义变量名:gmData,用于存储1993—2007年结核病发病数,共15个数据。gm(gmData,17);#调用函数,使用1993—2007年的作为训练样本,预测未来两年的结核病发病数,共17个数据。
预测出2008—2009年发病例数分别为34 437.39、37 475.49,结果见表3。
表3 灰色模型对重庆市2008年和2009年的结核病预测结果
Table3 Forecast results of tuberculosis by grey model in Chongqing city in 2008 and 2009

年份登记病例数预测结果误差20082709834437.3927.08%20092501037475.4949.84%
3 讨论
通过R语言的神经网络模型和灰色模型对结核病发病情况预测,结果发现神经网络模型对结核病发病人数的预测误差不超过5%,而灰色模型对结核病发病数的预测误差较大,分别为27.08%和49.84%。说明神经网络模型对于结核病发病情况预测的准确性远远高于灰色模型,是预测结核病发病情况的较优模型,这与易静等[7]研究结果一致。
从预测结果来看,R语言的预测结果并不亚于其他价格高昂的商业软件,商业软件具备强大的数据统计、分析、预测和周边数据处理等功能,若要完全或深入掌握商业软件各项功能的使用,需要耗费大量的时间和费用进行专门的培训。在实际分析预测的工作中,不会用到商业软件的所有功能。
本文采用免费开源的R语言中的神经网络分析模型和灰色模型完成分析与预测,并得到了满意的预测结果,相对于使用商业软件而言,可大大降低办公或科研成本。
研究表明,R语言能满足结核病发病数的预测需求,可推广到其他传染病发病数的预测或其他行业的数据分析与预测。下一步研究方向是根据决策需求和数据来源(如:《中国疾病预防控制信息系统(网络直报信息系统)》)将R语言的各个功能抽象化,通过高级编程语言(如:.net、Java等)将分析模型、数据源和需求有机地整合起来,提供一个图形化操作界面,形成一套易用的决策支撑与预测系统,为卫生资源调配、科研工作等提供可靠的决策支撑。随着计算机硬件技术和软件工具的持续发展,R语言也会在保持目前成就的情况下,通过不断改善计算环境,成为有力的科研工具[8]。
1 张忠海.关于结核病防治现状的思考[J].齐齐哈尔医学院学报,2011,32(7):1113-1114.
2 石发恩,任如山,蒋达华.R语言在消声器设计试验中的应用[J].金属矿山,2008,20(11):97.
3 Hiroyoshi Arai.A function for the R programming language to recast garnet analyses into end-members:Revision and porting of Muhling and Griffin S method[J].Computers& Geosciences,2010,36:406-409.
4 徐国祥.统计预测和决策[M].上海:上海财经大学出版社,2001:113-131.
5 梁智勇.用Matlab实现GM(1,1)灰色模型的供电量预测[J].电脑编程技术与维护,2009,16(24):93.
6 Robert I.Kabacoff.R in Action[M].New York:Manning Publications Co,2009:8.
7 易静,杜昌廷,王润华,等.弹性BP神经网络在结核病发病率预报中的应用[J].现代预防医学,2007,34(19):3699-3701.
8 罗玫,赵嵩正,蒋建洪.模糊综合评价模型的R语言实现[J].航空计算技术,2011,41(4):56.

