基于神经网络的质量控制图异常诊断*
□ 何 文 □ 同淑荣 □ 王克勤
西北工业大学 管理学院 西安 710129
控制图已被大规模应用于制造业过程质量的监测与控制。控制图通过过程质量数据的统计监测来识别过程质量的波动,确定过程质量是否受控,过程质量波动可以分为随机波动和异常波动。实践证明,随机波动不会对过程质量产生影响,是可以接受的;异常波动存在一定的异常源,并在质量控制图上以一定的模式表现出来。因此,可以通过对控制图模式进行检测来确定过程质量是否受控。
但是控制图并不能进一步给出引起控制图异常模式的原因,这给异因查找带来一定的困难。另外,控制图异常模式和异常原因之间的关系具有一定的模糊性,例如:一种控制图异常模式可能是由一种异常原因引起的,但也有可能是多种异常原因引起的;一种异常原因有可能引起一种控制图异常模式,但也有可能引起多种控制图异常模式。因此,控制图异常模式与异常原因存在着一对一、一对多和多对多的模糊不确定关系。针对以上问题,首先构建控制图异常模式集,并针对每种异常模式确定其异常原因,利用模糊神经网络实现控制图异常模式到异常原因的推理,并对神经网络推理得到的异常度进行排序,缩小异常原因查找范围,提高查找效率。
1 问题描述
1.1 控制图异常模式定义
根据小概率事件原则,定义控制图异常模式:当控制图上的点子是随机排列的时候,其发生的概率是很大的,所以认为过程受控;当控制图上点子呈现一定规律性的时候,经计算其发生的概率是很小的,那么可认为过程受到异常因素的干扰,认为过程失控,并根据点子呈现的规律性对其异常模式进行定义。在此基础上,利用隐藏在异常模式中的信息,确定引起每种异常模式的异常原因,建立每种异常模式与它对应的异常原因之间的映射关系。
质量控制手册[1-2]和大量文献都对控制图判异准则进行了归纳和总结,可发现一般由文献[3]总结的7条判异准则,本文结合其与小概率事件原则总结了如下6种基本异常模式进行研究。另外,基本异常模式又会相互交叉组成混合异常模式,混合模式形成的交叉形式过于纷繁复杂,比较好的研究方式是应用一定的数学方法,将其分解成基本异常模式进行研究,因此,不将混合异常模式纳入研究范围。本文研究的6种异常模式如下:
模式一:连续7点至少有3点接近控制限;模式二:连续7点出现在控制中心线同一侧;模式三:连续11点至少有10点落在中心线同一侧;模式四:连续7点不断上升或不断下降;模式五:连续15点集中在中心线附近;模式六:点子作周期变化。
1.2 异常模式与对应的异常原因映射关系构造
根据控制图异常模式内隐藏的信息,分析查找可能的异常原因,并建立它们之间的映射关系。
模式一、模式二、模式三中接近控制限、中心线同一侧等语言和数据都带有偏移的性质。过程质量中,影响质量的因素为 5M1E(人、机、料、法、测、环),据此在质量控制过程中从5M1E出发,可以总结找到引起这种数据偏移的偏移性异因[4-6]:工具损坏、原材料或供应商变化、机器设置调整、引入新的操作工或检测工。当然这些原因还可以继续往下分,在这里不再继续研究。 对上述异因进行定义:C11(工具损坏)、C12(原材料或供应商变化)、C13(机器设置调整)、C14(引入新的操作工或检测工)。基于以上关系建立的映射关系如图1所示(图中 F1、F2、F3分别代表模式一、模式二、模式三)。
模式四、模式五、模式六数据本身带有一定的趋势信息,在质量控制过程中,从5M1E出发总结找到可能引起这种本质变化的异常原因如下:新材料的逐步引进、工装夹具的松动、操作疲劳、工机具老化。对上述定义如下:C21(新原材料的逐步引进)、C22(工装夹具的松动)、C23(操作疲劳)、C24(工机具老化)。 当然,这些异常原因也是可以往下分的,不再研究。基于以上关系建立的映射关系如图2所示 (图中F4、F5、F6分别代表模式四、模式五、模式六)。
2 控制图诊断系统设计
2.1 诊断系统原理模型
该控制图诊断推理系统由输入、输出以及6个推理模块组成。每个推理子模块通过神经网络实现异常模式到异常原因的推理,推理过程包括输入数据、神经网络推理、输出数据、异常原因异常度排序。控制图诊断系统原理模型如图3所示。

▲图1 模式一、二、三与其对应的异常原因之间的映射关系

▲图2 模式四、五、六与其对应的异常原因之间的映射关系

▲图3 控制图诊断系统原理模型
人工神经网络是在对人脑抽象、简化和模拟的基础上构建的信息处理数学模型,由具有非线性映射能力的神经元以及连接神经元的权系数组成。人工神经网络不需要构造参数确定的推理方程,具有很强的自组织以及自适应学习能力,具有很高的容错性和鲁棒性,能实现这种异常模式到异常原因之间模糊不确定关系的黑箱推理。因此,系统的主题部分采用神经网络实现推理。
根据控制图异常模式中隐藏的模式信息,可以分析出影响其可能异常的原因。每种异常模式和它对应的异常原因之间的关系是模糊不确定的,无法采用准确的参数模型解决,根据神经网络的性质,用其作为连接每种异常模式和对应的异常原因之间的桥梁,异常模式数据作为输入,其对应的异常原因作为输出,实现推理。在此基础上,对推理结果按异常度大小进行排序,为异常原因的快速查找提供依据。为每种异常模式建立这种推理排序过程子模块,并进行集成,当某种异常模式出现时,调用它所对应的推理子模块,得到异常原因异常度大小并对其进行排序,最终实现异常原因的快速查找。
本文采用BP神经网络,原因在于BP网实现了很好的仿真以及实际应用,利于本系统实现更快的应用。另外,神经网络层数以及各层神经元个数都是通过实验获得的。
2.2 神经网络输入及输出
每个神经网络的输入分别为其对应的控制图异常模式数据,输入变量个数为其对应的控制图异常模式中规定的异常点数;其输出变量为异常原因的异常度,取值在(0,1)之间,神经网络训练用异常原因的异常度大小可通过专家打分方法获得。输出变量的个数为可能引起异常模式的异常原因的个数。隐含层节点的个数可以基于误差标准通过实验获得。
由以上叙述可知:(1)神经网络 1、2、3的输入输出变量分别为模式一、二、三对应的模式数据和异常原因(C11、C12、C13、C14),模式一、二的输入神经元为 7 个,模式三的输入神经元为11个,它们的输出神经元分别为4个;(2)神经网络4、5、6的输入输出变量分别为模式四、 五、 六对应的模式数据和异常原因(C21、C22、C23、C24),模式四的输入神经元为7个,模式五、六的输入神经元为15个,它们的输出神经元为4个。
2.3 诊断系统推理神经网络设计
采用4层前馈BP神经网络,在数据推理过程中,下一层的推理结果不会对上一层的输入产生影响。在MATLAB语言环境下,实现神经网络的创建、训练及仿真实验。下面以第四个子模块为例,说明推理诊断子系统的设计。
模块四的4层前馈BP神经网络如图4所示,包括输入输出层和2个隐含层。根据上文2.2可知,其输入神经元个数为7,输出神经元个数为4,隐含层的个数基于实验标准可以确定为28。

▲图4 模块四的神经网络结构
神经网络的激活函数采用BP神经网络中应用最为广泛的Sigmoid激活函数,其曲线形状是S型,输出值在[0,1]之间,其表达式为:

神经网络的MATLAB语言创建程序命令为:
net=newff(minmax (P),[28,28,4],{'tansig','tansig','tansig'},'traincgf');
其中P为输入向量,28、28、4分别代表2个隐含层和输出层神经元个数,traincgf为共轭梯度训练法训练函数。
3 神经网络仿真
下面以Monte-C公式法产生的机械厂罗拉件生产车间的质量检测数据作为训练和仿真数据,异常模式对应的异常原因的异常度可以通过专家打分方法获得。罗拉件的要求尺寸为35 mm,通过样本计算其3σ大小为1.262 mm(σ为标准差)。
异常原因数据是异常模式数据的根源,所以异常原因数据的类别决定着异常模式数据的自动分类和不同。为了便于说明神经网络的训练和仿真,将异常输出原因数据与其对应的异常模式数据进行分类 (异常原因数据的分类将自然而然地导致异常模式数据自然分类;实际中,训练用异常模式与异常原因数据只要能足够全面地反映过程质量各种状态,无需进行分类,可直接进行训练)。本文根据异常原因排序种类对其进行分类。模式四所对应的异常原因为4个,其排列顺序一共是24种,针对每种异常原因排列顺序各产生与其对应的50组异常原因数据以及异常模式数据,用于神经网络的训练和仿真。由于数据庞大,这里不再赘列。
为了防止训练过程中神经元的饱和,首先对数据进行标准化处理,再利用Min-Max函数进行处理,然后输入神经网络对其进行训练。在此基础上将输入模式数据进行标准化并输入神经网络获得输出层信号。本神经网络采用共轭梯度算法进行训练,学习率设为0.05,网络连接权值根据输出值和目标值之间的误差进行自动调整,训练结束条件设为均方误差小于10-4。训练误差曲线如图5所示。
下面针对24种异常原因输出类型,各选择一组数据进行仿真。仿真的实际输出和目标输出对比如表1所示。从表1中的对比发现,神经网络实际输出和目标输出的顺序是一致的,并且,实际输出大小和目标输出大小之间的误差都在5%以内,是可以接受的,不会对根据神经网络输出的结果查找异常原因产生本质的影响。利用训练的神经网络对新产生的异常模式进行推理,减少每次不必要的查找异常原因的重复工作,减少实际工作中的浪费,提高过程质量管理的效率。与其它方法相比:如参考文献[6]这类方法,模糊数以及模糊数之间映射规则的构建是得到推理结果的关键,需要得到确定的输入输出模糊数参数以及它们之间的映射规则,这种参数精确的模糊数,以及基于这种模糊数的模糊映射规则,很难和实际的异常模式到异常原因的推理关系相适应;而模糊神经网络不需要精确的参数,因其记忆学习功能,可以利用以前的经验数据进行训练,得到异常模式到异常原因的推理关系,因此,系统推理得到的结果比文献[6]这类模糊规则推理方法得到的结果更为准确、可信。
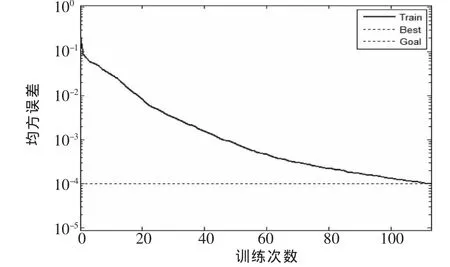
▲图5 训练误差曲线
4 总结
本文以神经网络为基础,构造控制图异常模式到异常原因的推理诊断系统,通过神经网络自动挖掘隐藏的异常模式与异常原因之间的映射关系,实现从异常模式到异常原因的推理排序,为过程质量管理中异常原因的查找提供帮助。通过仿真实验证明,系统具有很好的可靠性。在对异常原因异常度大小的确定方面,可以进一步通过引进模糊集合理论对模糊资料进行处理得到,使结果与实际更加相符。
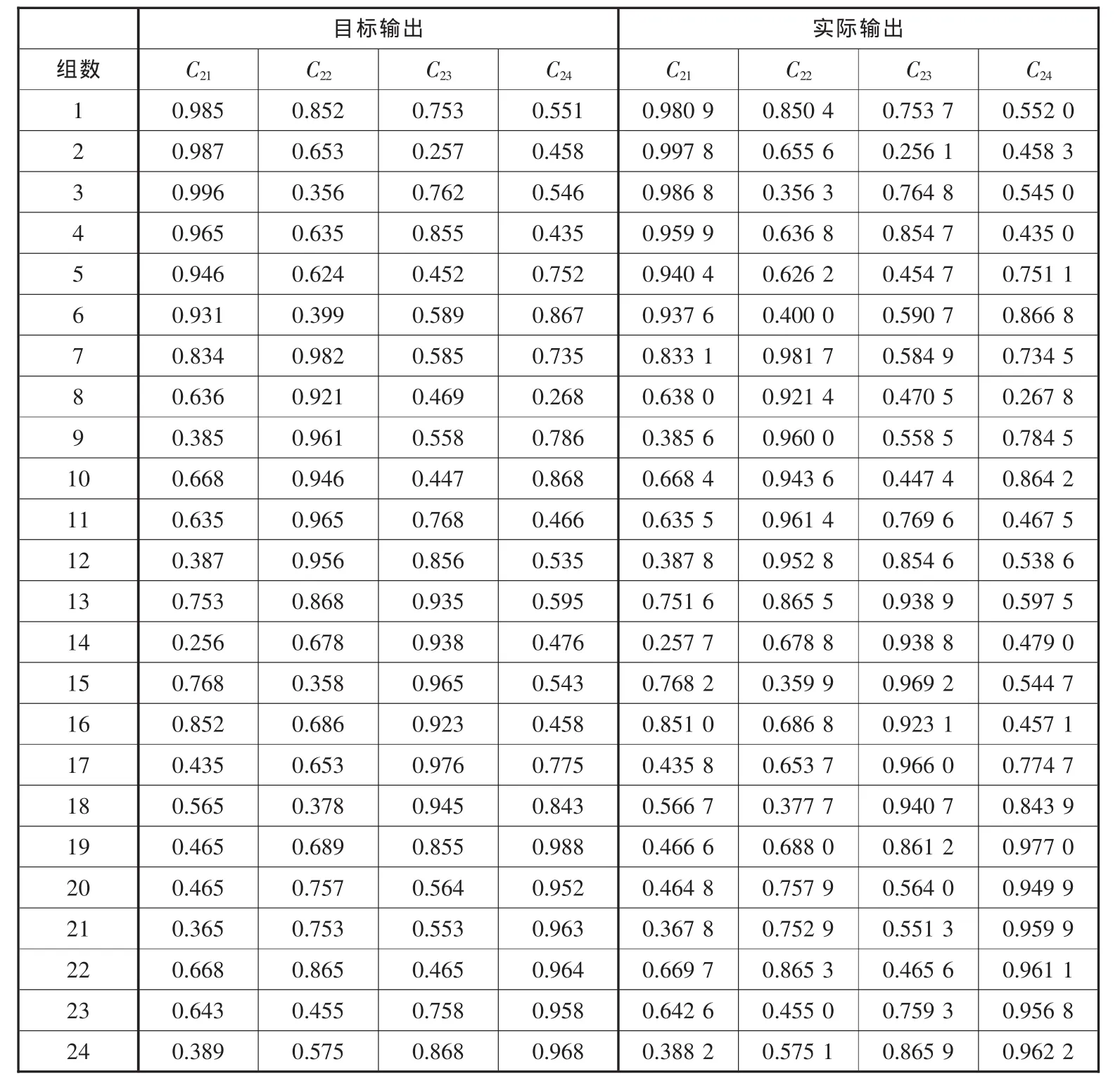
表1 仿真实际输出和目标输出对比表
[1] 钱钟侯,王成斌,孟玉科.多元质量控制[M].北京:中国铁道出版社,1995.
[2] 钱夕元,荆建芬.统计过程控制及其应用研究[J].计算机工程,2004,30(19):144-145,154.
[3] 徐文.一类基于模糊神经网络的控制图模式识别系统[D].北京:北京化工大学,2011.
[4] NELSONLS.The Shewhart Control Chart Test for Special Causes[J].Journal of Quality Technology,1984,16(4):237—239.
[5] GRANTEL,LEAVENWORTHRS.Statistical Quality Control[M].New York:McGraw-Hill Education,2002.
[6] 侯世旺,同淑荣,马飞.基于模糊质量阈值的质量控制图模糊诊断系统[J].计算机集成制造系统,2009,15(10):2039-2044.

