最小二乘直线拟合方法及其在同位素地质年代学中的应用研究
范文博,王文龙 ,陈岳龙,李大鹏
1) 中国地质大学(北京)地球科学与资源学院,北京,100083; 2)北京理工大学数学学院,北京,100081
内容提要:最小二乘法(least squares method)是直线拟合常用的方法,在自然科学和社会科学内被广泛应用,尤其在同位素地质年代学领域更是必不可少。仅考虑x或y误差的普通最小二乘法(normal/ordinary least squares)广为人知,但事实上最小二乘法并非如此简单,尤其是在同时考虑x、y误差(乃至误差相关)并采用加权处理时,其数学处理方法会变得十分复杂,而此时普通最小二乘法显得极不合理。本文在前人研究的基础上,结合同位素地质年龄计算的需要,对直线拟合的最小二乘法进行了系统地总结研究,详细介绍了普通最小二乘法、加权普通最小二乘法(normal/ordinary weighting least squares)、标准加权最小二乘法(standard weighting model)、标准独立加权最小二乘法(standard independent weighting model)、独立加权最小二乘法(independent weighting model)及误差相关最小二乘法(error correlated independent weighting model)的数学原理及相关变量的计算过程。在此基础上,进一步阐述了MSWD(mean squared weighted deviation)这个同位素地质年代学中经常使用的参数的数学意义,以及MSWD对计算结果的评判意义。准确理解这些数学方法,对于我们合理选择同位素地质年龄相关参数的计算方法,科学评价直线拟合结果并探讨其地质意义至关重要。我们的研究同时有助于拓展和完善数学领域最小二乘法的基本理论,并可用于其他领域相似的研究之中。
同位素地质年代学研究是确定地质体绝对年龄的主要手段,包括Rb-Sr、Sm-Nd、Re-Os、U-Th-Pb、K-Ar(Ar-Ar)等测年方法,在当前地质学领域内得到了广泛应用。在同位素地质年龄的计算中,常常需要根据一组样品的同位素测试结果进行直线拟合,最常见的是等时线拟合,主要有Rb-Sr、Sm-Nd、K-Ar、Re-Os、Pb-Pb等等时线。除此之外,U-Pb不一致年龄的计算,以及利用26Al-26Mg、129I-129Xe等绝灭了的放射性(extinct radioactivity)同位素方法研究陨石的相对年龄时,也要用到直线拟合。事实上,在地球科学内的诸多领域,都用到了直线拟合。
直线拟合常用的是最小二乘法,其在自然科学和社会科学领域内得到了广泛的应用。其所要解决的问题是:根据两个理论上存在线性关系的变量的几组测试数据点(多数情况下,这些数据点不见得恰好位于理论直线之上),寻找这两个变量之间的线性函数关系。当这些测试数据点与拟合直线的“偏差平方和”最小时,得到最佳拟合直线,即为所求。通常情况下,直线拟合多数采用最简单的普通最小二乘法,这也是诸多数学书籍中介绍最多、并被多数人所熟知的直线拟合方法(例如中国科学院数学研究所数理统计组,1974;张启锐,1988;周复恭和黄运成,1989;张小蒂,1991;周纪芗,1993;吴翊等,1995;李庆阳,2001;同济大学应用数学系,2002;盛聚等,2008;周惟公,2008;王黎明等,2008;褚宝增和王翠香,2010;何晓群和刘文卿,2011)。这种方法隐含地假设变量x不存在误差,并将所有误差都归于变量y(类似,可将所有误差都归于变量x),即便在x和y同为测量值的情况下,此时普通最小二乘法在确定未知参数及估计其真实误差方面,失去了准确性(Borcherds and Sheth, 1995; Sheth et al., 1996)。
仅考虑x或y误差的普通最小二乘法广为人知,但实际上最小二乘法并非如此简单,尤其是在同时考虑x、y误差(乃至误差相关)并采用加权处理时,其数学处理方法会变得十分复杂,而这对于许多应用同位素地质年代学方法进行地质学研究的人来说,都十分陌生。之所以会如此,主要有两方面的原因:① 数学处理方法的复杂性以及相关资料的相对缺乏;② 采用已有的软件(Isoplot)而“无需”思考其数学原理。
虽然同位素地质年代学方法被广泛应用,但地质学研究者多热衷于年龄结果本身的地质意义,同时由于同时跨越了数学和地质学两个学科,因此很少有人同时结合地质需要、对最小二乘法的数学原理作系统深入的总结介绍。如前所述,许多数学书籍也只涉及最简单的普通最小二乘法,何晓群和刘文卿(2011)、费业泰(2010)对考虑加权的最小二乘法也只是做了简单介绍。李志昌等(2004)介绍了York(1966,1969)、McIntyre 等(1966)算法的一部分,而更多的同位素书籍(韩吟文和马振东,2003;陈骏和王鹤年,2004;陈岳龙等,2005;陈道公等,2009),则忽略具体算法而只强调MSWD(见下文介绍)对等时线拟合结果评价的用处。事实上,想要真正了解MSWD对拟合结果的评判意义,就必须对最小二乘法本身有所把握。国外一些学者在前人[如Deming,1943;据York(1966),Borcherds and Sheth(1995)所述]研究的基础上,对最小二乘法的数学算法及相关问题作了进一步的研究和探索(如McIntyre et al., 1966; York, 1966, 1967, 1969; Brooks et al., 1972; Titterington and Halliday, 1979; Borcherds and Sheth, 1995; Sheth et al., 1996; Mahon, 1996; Bruzzone and Moreno, 1998),取得了突破性进展。但这些研究各有新的尝试和侧重,同时难免存在着一些分歧、甚至错误,因此想要系统了解最小二乘法并非易事。Ludwig(2008)开发的Excel加载宏Isoplot,提供了同位素年龄计算的一个很好的平台,其以York(1969)、Titterington和Halliday(1979)、Brooks 等(1972)等的算法(Ludwig,2008)为基础,但未对具体数学方法作详细介绍。这样的话,虽然Isoplot被广泛使用,但相关同位素年龄的计算方法,对多数地质学研究者来说仍然是一个“谜”。正如Allegre(2008)所述,如今相关测试方法已经有了很大的进步,而理论模型——或许是统计模型应该跟上分析方法前进的步伐,这点十分重要,但事实并非如此,这使得我们不得不思考如何对待通过自动化的分析方法已经积累的大量数据。可见,将最小二乘法这个在同位素地质年代学内普遍应用的统计方法“显性化”,是非常有意义的,这也有助于解决实际研究中存在的一些困扰,例如如何理解MSWD对年龄结果的评价及参考意义。
鉴于此,以下将在前人研究的基础上,结合同位素地质年龄计算的相关知识,对直线拟合的最小二乘法作详细总结和研究,并进一步在此基础上讨论同位素地质年代学应用的相关问题。
1 相关测年原理简介
首先以Rb-Sr等时线法为例,介绍应用最小二乘法所要解决的地质问题。核素87Rb通过一次β-衰变变成稳定同位素87Sr,根据放射性衰变定律,进一步推演得到
87Sr=87Sr0+87Rb(eλt-1)(Faure,1986)
式中,λ为87Rb的衰变常数,t为从同位素体系封闭到现在的时间,亦即所求的地质年龄。而87Sr、87Sr0和87Rb均表示物质的量,即是以mol为单位,本当写为n(87Sr)、n(87Sr)0和n(87Rb), 但本文中太多,为简便计写为现式,后边其他同位素亦仿此处理。
两边同时除以稳定核素86Sr的含量,得:
此式为Rb-Sr同位素定年的基础,其中87Rb/86Sr、87Sr/86Sr为现今样品的实测同位素含量比值,(87Sr/86Sr)0为距今t时刻时这两种同位素的初始比值。由于 (87Sr/86Sr)0未知,因此不能直接计算年龄。对于一套同源、同时、封闭的样品,其87Sr/86Sr 初始值均一,也就是不同样品间的(87Sr/86Sr)0一致,而其距今t时刻时的87Rb含量可能不同,从而导致放射性成因累积的87Sr含量不同。这样的话,这一套样品内的不同样品之间,87Rb/86Sr、87Sr/86Sr就会有所差异。这时,t、λ为常数,上式便可看作直线方程
y=a+xb(Faure,1986)
这里b=eλt-1,y=87Rb/86Sr,x=87Sr/86Sr。
对于上述一组样品,根据其(87Rb/86Sr,87Sr/86Sr)测试值及其误差,运用最小二乘法拟合直线,就能够得到其斜率与截距。根据斜率b=eλt-1,就可得到所关注的年龄t,而其截距则为(87Sr/86Sr)0,可用于同位素地球化学示踪。
除Rb-Sr同位素体系之外,Sm-Nd、K-Ar、Re-Os同位素体系定年也常用到等时线法,其同位素定年方程分别为(Faure,1986) :
对于U-Pb同位素体系,最小二乘法直线拟合主要用于Pb-Pb等时线拟合以及U-Pb谐和图中的不一致线拟合。前者的斜(率)截(距)式直线方程为(Rosholt et al., 1973; Faure, 1986; 陈道公,2009):
后者的点斜式直线方程为:
(Wetherill, 1956; Allegre, 2008)
在应用绝灭了的放射性同位素对陨石进行相对年龄测定时,同样需要首先用到直线拟合,如26Al—26Mg、129I—129Xe陨石测年,其对应直线方程分别为:
(Allegre, 2008)
综上可知,这里所要解决的问题是,根据样品的一组同位素比值测试数据(往往带有实验误差)(xi,yi),i=1,2,3,…,n,选择最优的最小二乘法处理模型,拟合最佳直线并计算斜率、截距及其误差,并进一步根据拟合结果,尽可能地甄别、评判其是否有真正的地质年代意义。
2 直线的最小二乘法拟合
现给出样品的一组同位素比值测试数据点(xi、yi),i=1,2,3,…,n(n>2),据此求自变量x和因变量y之间的函数关系L:y=a+xb。其中a、b为待定参数,当拟合直线与数据点之间的(加权)偏差平方和S最小时,得到最佳拟合直线。关于偏差平方和,根据York(1969),有两种等价的最一般形式:
(1)
(2)
这里(xi,yi)是第i个测试值,(Xi,Yi)是对应的调整值(图1),即最佳拟合直线上对应的点。

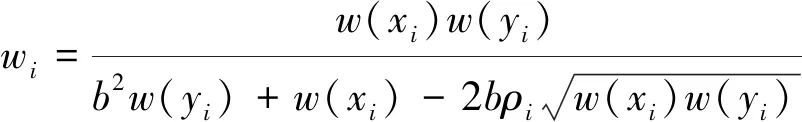
(3)
ρi为第i个点x和y变量的误差相关系数(error correlation,详见误差相关最小二乘法部分),对于U-Th-Pb测年,由于纵横坐标变量xi、yi是同时同步测试的,往往需要考虑误差相关系数,而对于其它测年方法,在实际应用中多不考虑这个参数。
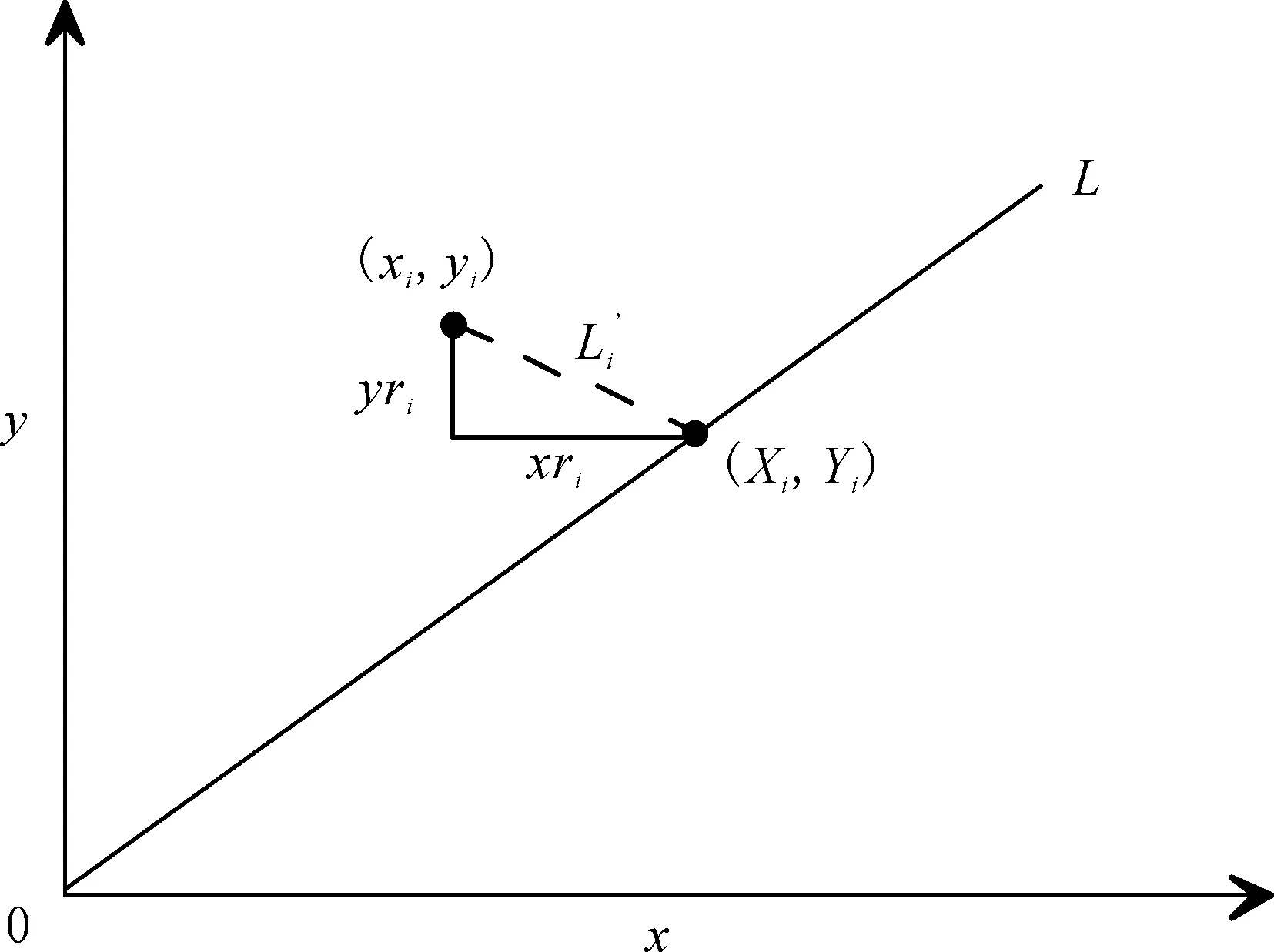
图1 最小二乘拟合中,相关量之间的一般几何关系Fig. 1 Illustration of relationship between various variables in least squares fitting of a straight lineL为最佳拟合直线,L′为调整线,(xi,yi)为测试点,(Xi,Yi)为对应调整点,yri表示y方向的残差,xri表示x方向的残差L is the best straight line,L′ is the adjustment line,(xi,yi)is the data point while(Xi,Yi)is the adjustment point corresponding. yri denotes residual in y direction,and xri in x direction
当ρi=0时,x、y的误差不相关,这时得到York(1966)、Borcherds和Sheth(1995)中所提到的Deming(1943)所定义的偏差平方和的公式,即与(1)式对应的(4)式,以及McIntyre 等(1966)、Wendt(1969)[转引自Brooks, 1972]、Borcherds和Sheth(1995)、Sheth等(1996)、何晓群和刘文卿(2011)所用的与(2)对应的(5)式,
(4)
(5)
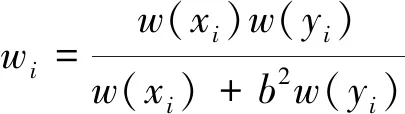
(6)
图1给出了拟合直线与相关量之间的一般几何关系。L为最佳拟合直线y=a+xb,连结测试点(xi,yi)与(Xi,Yi)的直线Li′为调整线,其斜率为每个点的y方向残差(yi-residual,以下用yri表示)与x方向残差(xi-residual,以下用xri表示)之比,即
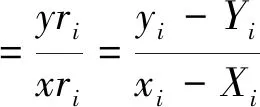
(7)
可以看出,随着拟合直线(即参数a、b)的变化,S也会相应地发生变化,当S取最小值时,所有点沿各自调整线回归到拟合直线上的距离之和最短,这时就得到了最佳拟合直线。方便起见,这里定义最佳拟合直线所对应的S的最小值为S*。以下从最简单的普通最小二乘法开始,逐步深入,分别介绍基于不同假设所得到的最小二乘直线拟合方法。实际应用中,则需要根据数据本身特征,选择最适合的最小二乘法进行直线拟合。
2.1 普通最小二乘法(normal/ordinary least squares)
顾名思义,这是介绍并使用最多的最小二乘拟合方法(例如吴翊等,1995;同济大学应用数学系,2002;李庆阳,2001;盛聚等,2008;王黎明等,2008;褚宝增和王翠香,2010;何晓群和刘文卿,2011),在Isoplot被广泛使用之前,等时线拟合多用这种方法[如申浩澈(1983)所述]。假设xi不存在误差(xi=Xi),yi存在误差(yi≠Yi),令wi=w(yi)=1(可认为w(xi)=),这时所有数据点沿与y轴平行的调整线调整到最佳拟合直线(图2a),
(8)
对于固定的一组数据,(8)式是S关于a、b的二元函数,根据多元函数的极值条件(同济大学应用数学系,2002),分别对S求关于a、b的偏导数,并令其为0,得:
进一步变换得到所谓的“法方程”或“正规方程”,
(9)
(10)
据(9)、(10),解得(吴翊等,1995;王黎明等,2008;盛聚等,2008;何晓群和刘文卿,2011):
(11)

(12)
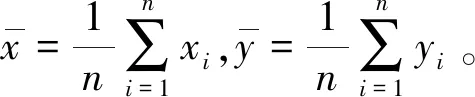
与之类似,也可将所有的误差都归于xi(xi≠Xi,yi=Yi),令w(xi)=1,wi=w(xi)/b2=1/b2(可认为w(yi)=),进行处理,如图2b。
对于一些研究对象,普通最小二乘法假设一个变量不存在误差,这是成立的。而对于同位素地质年代学,由于所有xi、yi都是测试值,这点显然不成立。笔者认为,对于Rb-Sr等时线法,考虑到87Rb/86Sr的测试误差往往比87Sr/86Sr的误差大许多,因此采用将所有误差归于87Rb/86Sr的(加权)普通最小二乘法,或许是可以接受的。Sm-Nd等时线法类似。
2.2 加权普通最小二乘法(normal/ordinary weighting least squares)
这是对普通最小二乘法的改进,与前者不同的是其给予每个点不同的权重。假设xi不存在误差(xi=Xi),yi存在误差(yi≠Yi),这时wi=w(yi)=1/σ2(yi)(可认为w(xi)=),所有调整线都平行于y轴(图2a),
(13)
同理,可以根据∂S/∂a=0,∂S/∂b=0,解得(Bruzzone and Moreno, 1998):
(14)

对(14)式中b的表达式进一步变换可得:
(15)
类似,也可将所有的误差都归于xi(xi≠Xi,yi=Yi)并采用加权处理,令w(xi)=1/σ2(xi),wi=w(xi)/b2(可认为w(yi)=),进而确定最佳拟合直线(如图2b)。
2.3 标准加权最小二乘法(standard weighting model)
普通最小二乘法以及加权普通最小二乘法的一个显著缺陷是只考虑一个变量的误差,在同位素年代学研究中,两个变量都是测试值,从而不可避免都存在误差,这显然不够精确。

(16)
同上,令∂S/∂a=0,得
(17)
令∂S/∂b=0,得:

(18)
将(17)式代入(18),化简会得到关于b的一元二次方程,解之并取其中一个解,得到:
(19)
a的解法同上,由最佳拟合直线过重心计算得到[(17)式,与(12)式本质相同]。
2.4 标准独立加权最小二乘法(standard independent weighting model)
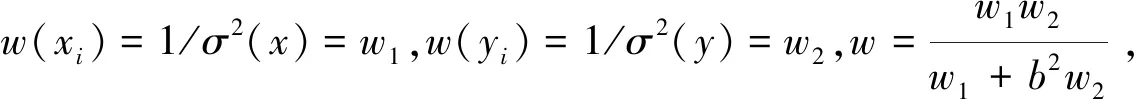
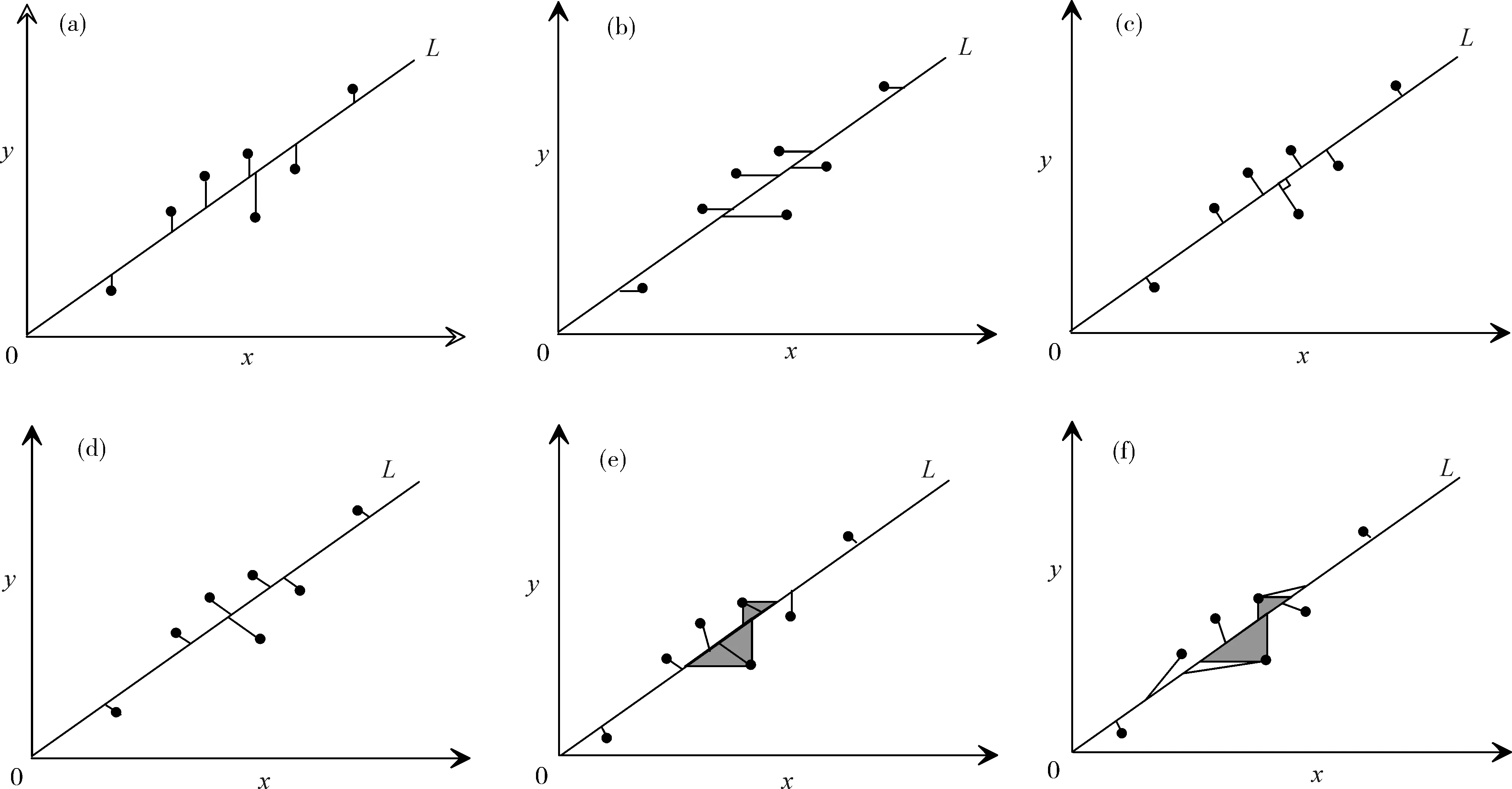
图 2 不同类型的最小二乘拟合方法中,数据点的调整方式:(a)(加权的)普通最小二乘模型,只考虑纵坐标的误差,所有调整线都平行于y轴,需要说明的是,对于同一组数据点,加权的普通最小二乘拟合与普通最小二乘拟合所拟合直线可能会不同;(b)(加权的)普通最小二乘模型,只考虑横坐标的误差;(c) 标准加权模型,所有调整线都互相平行且垂直于最佳拟合直线;(d)标准独立加权模型,所有调整线都互相平行;(e)独立加权模型,一般情况下,不同数据点的调整线不平行,但限制在三角阴影区内;(f)误差相关的加权最小二乘拟合模型,同样不同数据点的调整线不再平行,但调整线不再限制在三角阴影区内(参考York, 1966, 1967, 1969; Borcherds and Sheth, 1995; Sheth et al., 1996; Mahon, 1996; Bruzzone and Moreno, 1998,有增改)Fig. 2 Various types of adjustments in different models of least squares fitting: (a) normal/ordinary least squares and normal/ordinary weighting least squares, only the errors in y direction are considered. It should be noted that weighting least squares may have different results from the not-weighting in this situation; (b) normal/ordinary least squares and normal/ordinary weighting least squares, only the errors in x direction are considered; (c) standard weighting model, all the adjusting lines are parallel to each other and are perpendicular to the best fitting line at the same time; (d) standard independent weighting model, the adjusting lines are parallel to each other; (e) independent weighting model, the adjusting lines are not necessary to be parallel but should be situated within the shadow area; (f) error correlated independent weighting model, the adjusting lines are not necessary to be parallel or be restricted within the shadow area(after York, 1966, 1967, 1969; Borcherds and Sheth, 1995; Sheth et al., 1996; Mahon, 1996; Bruzzone and Moreno, 1998)

(20)
令∂S/∂a=0,∂S/∂b=0,同上解得:
(21)
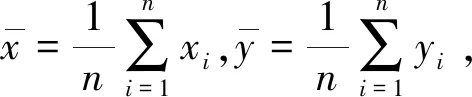

(22)
S的最小化给出关于b的二次方程,解之并选取其中一个合适的根作为拟合直线的斜率,得到(Bruzzone and Moreno,1998):
(23)
这里b*指(14)中的b,即对于此组数据,假若xi没有误差时计算所得的斜率。S、Sx、Sy、Sxy、Sxx、Syy如2.2节中所述。
2.5 独立加权最小二乘法(independent weighting model)
这是双变量最小二乘拟合的更一般情形,其同时考虑每个点xi、yi的不确定度,并认为σ(xi)、σ(yi)二者之间不存在确定的数学关系。与上述2.1~2.4节的情形不同,此时调整线一般不再平行,并被限制在假设x、y都不存在误差时的竖直和水平调整线以及最佳直线所包围的三角形内(图2e),而且得不到斜率b和截距a的解析解,必须使用迭代法,寻找认为达到我们所需要精度的近似解。下面给出两种处理办法。
2.5.1 独立加权模型解法一
York(1966)从表达式(4)着手解决这个问题,延续其思路,以下进一步更详细地解析相关过程:
2.5.1.1 步骤 1
S是关于Xi、Yi的泛函,根据泛函极值条件及相关运算法则,当S取得极值时,其一阶变分为0,即有:

(24)
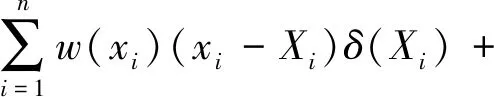
(25)
这里δs、δ(xi)、δ(yi)分别表示S、xi、yi的一阶变分[此概念来自“变分法”这一数学分支学科,而变分法则是研究求泛函极大值和极小值的方法,简单理解,“一阶变分”类似于高等数学中的微分,有关其详细的数学定义可参考老大中(2004)、邵克勇等(2011)]。
由于(Xi,Yi)位于最佳拟合直线上,因此有:
Yi=a+bXi
(26)
两边同时求变分,得到:
δa+Xiδb+bδ(Xi)-δ(Yi)=0
(27)
对于不同的i,(27)式乘以各自的一个未定乘数λi,并求和,得到:

(28)
(25)+(28),得:

(29)
令δ(Xi)、δ(Yi)、δa、δb的系数为0,得到:
(30)
(31)
(32)
(33)
将(30)、(31)分别代入(26)中,分别替换Xi、Yi,得到:
(34)
由(34)式解出λi,得到:
λi=wi(yi-a-bxi)
(35)
wi由(6)式给出。
2.5.1.2 步骤2
现在,(32)、(33)、(35)一共有(n+2)个等式,(n+2)个未知数:a、b和λi。根据(32)和(35),有:
(36)
根据(33)和(35),有:
(37)
将(30)代入(37),替换Xi,得到:
(38)
进一步化简,有:

(39)
将(35)式代入(39)式,替换λi得到:

(40)
这里可以通过(36)、(40)同时解出a、b。
2.5.1.3 步骤 3
现在,从等式(36)中解出a,得到[与(12)式形式相同]:
(41)
这里
(42)
将(41)式代入(40)式,化简即得到York(1966)的“最小二乘立方方程”。事实上,正如Mahon(1996)所认识到的,由于wi中也含有b,因此这也只是一个形式上的立方方程:
(43)
(43)式中,左边第一项系数化为1,得:
b3-3αb2+3βb-γ=0
(44)
其中
(45)
(46)
(47)
将(44)式看作一元三次方程,得到其三个实根为:

这里
York(1966)指出b3是我们所需的根,因此:
(48)
由于α、β、γ都含有wi,而wi中也含有b,因此并不能直接从(48)式中解出所需的斜率b。这时就需要用到方程求根的迭代法(参见李庆扬,2001),用计算机编程计算(参见彭国伦,2002)。简要说明其原理:
① 首先给出一个b的近似值b(1),代入(6)计算wi并将所得代入(45)、(46)、(47)计算α、β、γ,进一步将所得代入(48)得到b(2);
② 将b(2)代入(6)计算wi并将所得代入(45)、(46)、(47)计算α、β、γ,进一步将所得代入(48)得到b(3);
③ 依次重复以上过程,直到b(k+1)-b(k)<ε。这里ε是一个我们可以接受的、使得b(k+1)与bk接近几乎完全相等的数值,取决于我们所要求的斜率b的精度。b(k+1)即为所求斜率b。
这时,a同样由(12)式(也就是(41)式)解出。
将(30)、(31)代入(7)式,得到一个极有意义的表达式(York,1967),
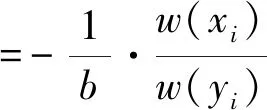
(49)
据此可以确定调整线的方向,可以看出,调整线的斜率与最佳拟合直线的斜率b符号相反,亦即调整线位于图2 所示的三角阴影区内。此等式对于2.1节至2.5节都成立。
2.5.2 独立加权模型解法二
其它学者(McIntyre et al, 1966; Wendt, 1969,转引自Brooks, 1972; Borcherds and Sheth, 1995等)则从公式(5)着手,根据S取最小值时的条件,得出斜率和截距的计算办法。下面我们尝试推导,
令∂S/∂a=0,得:
(50)
令∂S/∂b=0,得:
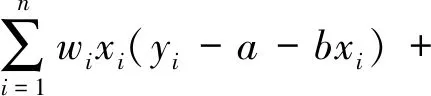
(51)
将(50)代入(51),化简得到:
(52)
同样可将(52)式看作关于b的三次方程,用上述类似的迭代法处理即可。
Borcherds和Sheth(1995)并未先将(50)式代入(51),而是将解三次方程的复杂性转移到迭代过程中去。根据(51)化简得到一个二次方程:
Ab2+Bb+C=0
(53)
其中
A=a∑w2(yi)w(xi)xi-∑w2(yi)w(xi)xiyi
B=a2∑w2(yi)w(xi)-2a∑w2(yi)w(xi)yi
C=∑w2(xi)w(yi)xiyi-a∑w2(xi)w(yi)xi
这时开始用迭代法:
① 用普通最小二乘法得到b的初始值b0,代入(50)计算a,用这个a代入(51)式,计算得到b的两个根。② 将b的两个根及①中a代入(5)分别求S。选择较小的S对应的b作为新的b值,记为b1。③b1再代入(51)式,计算得到b的两个根,与②类似处理,得到b2。依次重复,得到b(j),直到b(k+1)-b(k)<ε。ε与2.5.1节中相同。这时的b(k+1)与对应的a即为所求。
2.5.3 独立加权模型与其它最小二乘模型的关系
可以认为2.1~2.4节所述的四种模型是2.5节中的独立加权最小二乘模型的特殊情形,虽然如此,但由于前四种情形下,能够得到斜率b的解析解,而且实践中会有与之类似的问题,因此详细讨论是有必要的。而独立加权最小二乘模型则无解析解,需用迭代法进行数值计算。
2.1~2.4节以及2.5.2节都是用偏导数为0作为取得极值的条件进行推导的,因此其解是相通的;而2.5.1节则采用变分法得到,给定2.5.1节中(43)式不同的条件,进一步演算,则可得到公式(11)、(15)、(20)、(22)。
2.6 误差相关最小二乘法(error correlated independent weighting model)
York(1969)将独立加权模型进一步复杂化,提出了(1)(2)两种计算公式,并引进误差相关(系数)ρi误差相关这个参数,即σ(xi)和σ(yi)之间的线性相关系数,ρi1,当其取0时,σ(xi)和σ(yi)相互独立;当其绝对值为1时,说明其完全线性相关,+1意味着正相关,-1则负相关(Ludwig,2008;梁晋文,2001;费业泰,2010;褚宝增和王翠香,2010)。通常所见的U-Pb谐和图中,误差椭圆的方位也就是误差相关系数的反映。对于此种最小二乘法,不仅考虑每个点的误差,而且考虑每个点纵横坐标误差之间的相关系数,这时所有测试点的调整线一般不平行,且不会限制在上述2.5节中所述的阴影三角形内(图2f)。
与2.5节类似,也可以从(1)式着手,令S的一阶变分为0,或从(2)式着手,分别对a、b求偏导数并令其结果为0,推演b的计算过程。这里不再做详细推导,其具体原理同上。York(1969)从(2)式着手,得到的最小二乘平方方程为:
(54)
据此的最佳拟合直线斜率为:
(55)
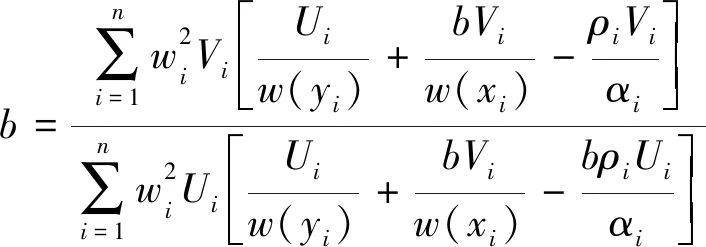
(56)
其中:
wi由(3)式给出。
x、y的残差分别为:
(57)
(58)

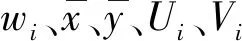
3 相关参数的误差估计
关于最佳拟合直线的斜率b和截距a的误差(标准差)计算,较多采用的是误差传递公式(McIntyre et al., 1966; York, 1966, 1969; Brooks et al., 1972; Kullerud, 1991; Mahon, 1996),而York(1969)所给的误差公式则存在错误(Titterington and Halliday, 1979; Mahon, 1996)。Titterington and Halliday(1979)用最大似然法所讨论的结果与误差传递公式的计算结果相同。Sheth等(1996)则提出了另一种标准差的计算方法。无论哪种算法,都是对标准差的近似估计,这里主要介绍前者。而另一个至关重要的问题是在得到标准差后,如何确定置信区间。
3.1 标准差的计算
这里以误差相关的最小二乘模型为例介绍,其它模型可以通过相关参数取特殊值得到,也可用类似的方法进行推导。记(56)式为F(b,xi,yi)=0,即:
(61)
根据误差传递公式(省略泰勒序列的高次项),有(Titterington and Halliday, 1979;Mahon,1996;费业泰,2010):
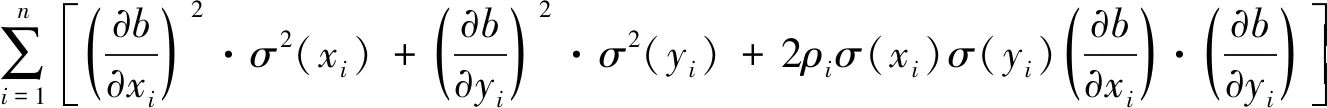
(62)
根据隐函数求导公式(同济大学应用数学系,2002),
(63)
以上两式联立,就可得到Mahon(1996)所用的公式:
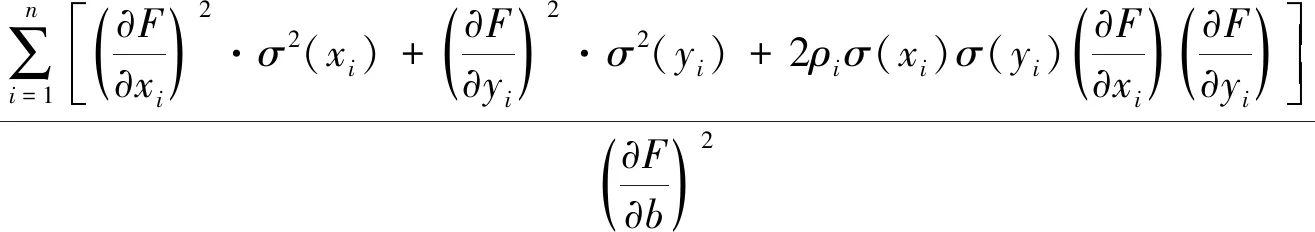
(64)
或

(65)
对于截距a的误差,也可采用类似的方法,将(12)式看作关于xi、yi的函数,有:

(66)
将∂F/∂xi、∂F/∂yi、∂F/∂b、∂a/∂xi、∂a/∂yi代入(64)(66)式,得到以下两式(Mahon, 1996; Titterington and Halliday, 1979):
(67)
(68)
York(1969)中认为可以将点关于最佳拟合直线的分散程度考虑在内,进行误差估计,得到扩展的不确定度(York, 1966,1969; Kullerud, 1991),即:

(69)
有关MSWD的介绍见下。Mahon(1996)认为这种做法是从数学角度来说是不严格的,如果MSWD小于1的话,就会降低误差。因此在实践中如若用到,一定要指明。
3.2 确定置信区间
通常给标准差(σb和σa;代表68%的置信区间)乘以2(更准确地说是1.96,表1),得到斜率b和截距a95%的置信区间。事实上,这样做的前提是用于进行等时线拟合的样品数据点足够多(即n较大),且斜率和截距的计算结果服从正态分布。这时,平均值附近的2σ(1.96σ)区间,代表了概率密度曲线中95%的面积区域。当拟合数据点较少时,就需要乘以t-分布的α(这里取0.025,对应于95%的置信区间)分位点tn-2(α=0.025)(参见褚宝增和王翠香等,2010)(Mahon, 1996; Ludwig, 2008)。 这时:
b=b*±tn-2(α=0.025)·σb,a=a*±tn-2(α=0.025)·σa(b*表示最佳斜率,a*同)。
当数据点较少时,斜率的误差会非常大,正因为如此,Ludwig(1998, 2000, 2003, 2008等)一直强调避免3点或4点等时线。
4 MSWD
根据Wendt和Carl(1991),MSWD(mean squared weighted deviation)计算方法为
(70)
其中f=n-k,为自由度,对于加权且固定截距的线性回归,k取1,而对于无限制条件的线性回归,k取2(Mahon, 1996),n表示拟合所用的数据点数目。wi如(3)式或(6)式所示。据此可知,这里:
(71)
即最佳拟合直线所对应的偏差平方和(S*)的平均值。根据以上3中的讨论可知,S*的大小反映了所有数据点偏离最佳等时线的总距离,当所有数据点严格位于最佳等时线时,S*取值为0,当然MSWD也为0,当然这种情况是绝对理想化的。

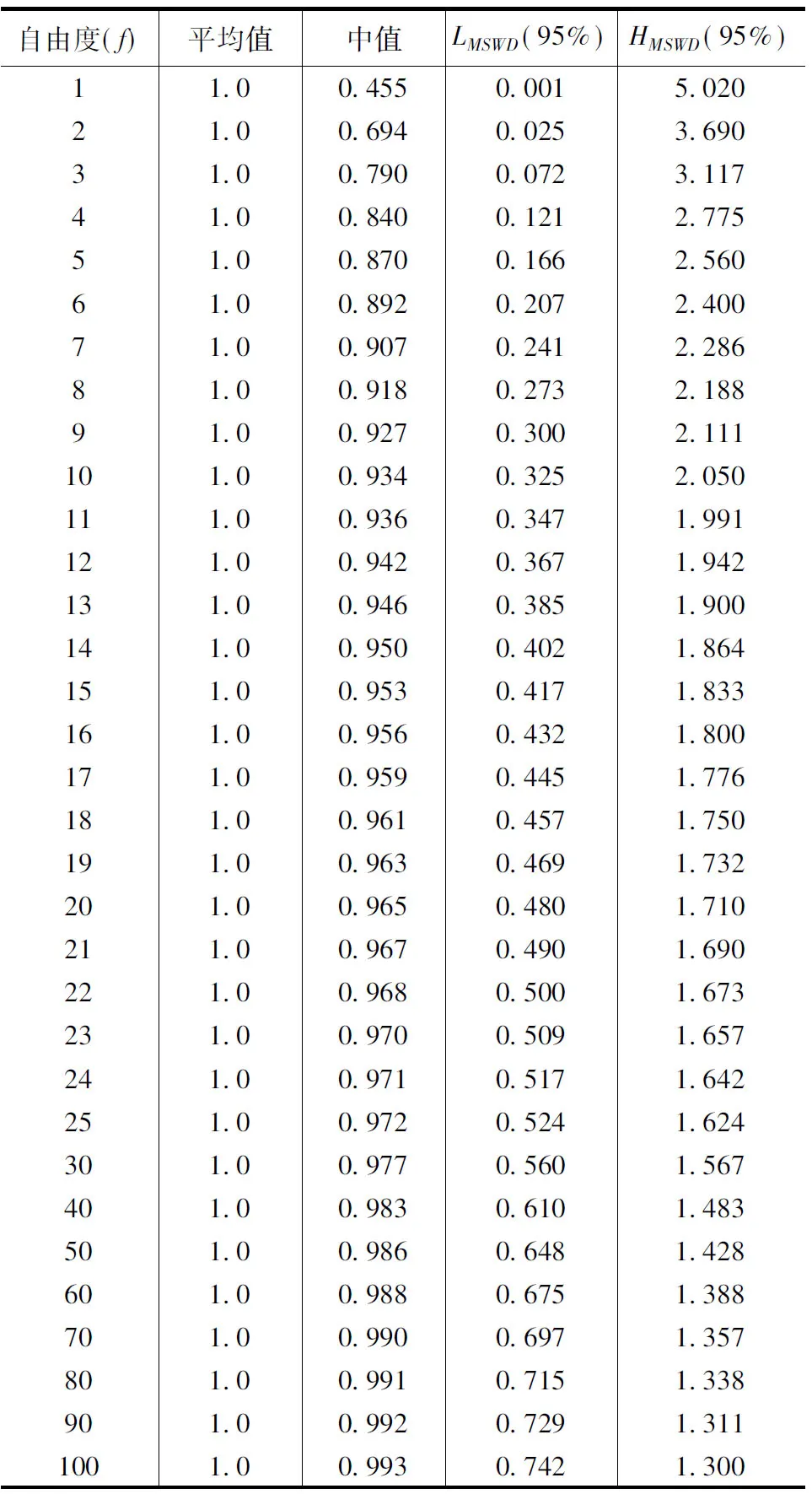

接下来一个重要的问题是在同位素地质年代学中,如何应用MSWD对拟合结果进行解释。通常可能会这样认为,当测试所得的MSWD小于对应自由度的HMSWD时,说明拟合效果较好,具有地质意义;反之高于时,则需要重新考虑是否样品完全符合测年条件。是否如陈骏和王鹤年(2004)所述“当MSWD>2.5时,很可能是一条误差等时线”,或如韩吟文和马振东(2003)所述,“该值越小,等时线质量越好。当存在地球化学误差时,MSWD>1;当不存在地球化学误差时,MSWD≤1”。问题似乎并没有这么简单,Kalsbeek (1992)、Wendt (1992)对此已经做了一些讨论。
首先,需要明确的是,MSWD值明显受对实验分析误差估计准确性的影响(陈道公,2009;这点可从公式(70)与(1)至(6)明显地看出),只有在使用最小二乘法(或最大似然法)拟合等时线,且对数据点的误差估计准确时,MSWD才可作为检验拟合结果的参数(Mahon, 1996)。但实际研究工作中,这点并没有得到重视,笔者查阅了一些近年来用Rb-Sr等时线法测年的文章发现,许多文章并未交代等时线拟合中相关变量的(分析)误差估计,却使用MSWD对拟合结果进行评价,如李真真等(2009)、李光来等(2011)、张臣(1998)、蓝廷广等(2011)、祝禧艳等(2010)、周雄等(2010)、陈江峰等(2003)、魏俊浩等(2003)、毛光周等(2008)。而给出了误差的文献中,对分析误差估计的方式依然存在着不明确性。李秋立等(2006)明确指出拟合时,87Rb/86Sr比值采用2%误差、Sr同位素比值采用保守外精度误差0.05%;姚海涛等(2001)选用87Rb/86Sr 、87Sr/86Sr 的分析误差分别为1.5%、0.02%,并提及这是“一般的全岩Rb-Sr等时线法定年的分析误差”;杨进辉和周新华(2000)则只提及87Rb/86Sr的输入误差为0.5%~2%。
其次,根据上述3、4部分的详细介绍可知,这里仅考虑了实验分析误差,且给出了仅由分析过程中的随机误差引起数据点对最佳拟合直线偏离时,MSWD的概率分布情况。但事实上,数据点对最佳拟合直线的偏离(甚至靠近),不仅可能来自实验分析误差,而且还有可能来自地质背景、每个样品本身、以及测年方法的选择,但对于除实验分析误差之外的其它误差,目前似乎并没有合理的方法将其定量化(Allegre, 2008),因此在拟合时,也仅考虑了实验测试误差。实际研究中所用样品,更多地是接近而非完全满足同位素测年所需的条件,这就必然降低MSWD对拟合结果的评判意义。以等时线法为例,测年样品不一定真正具有完全相同的初始同位素比值(见Zheng, 1989),同位素体系能够在所研究对象内不一定能够完全封闭。这样的话,一方面,95%的置信边界只是表明当数据点的分散仅是由测试过程中的随机误差所引起时,MSWD会有95%的可能性落在这个区间内,但并不排除存在其它因素导致MSWD落入这个区域的可能性,并且这种可能性有多大是未知的;另一方面,对于MSWD落入其95%置信区间外的情况,也有可能是可以接受的。
基于此,在应用同位素地质年代学方法对地质体进行年代测定时,需尽量选择符合所用方法基本假设的样品,并且尽可能地准确估计分析测试误差。在此基础上,当MSWD落入95%的置信区间内时,说明测试结果线性相关程度良好,在尽可能地降低其他因素影响的情况下,所获年龄具有较大的参考意义。而当MSWD落入95%的置信区间外时,且测试误差估计准确、MSWD不至于过大时,拟合结果仍有一定参考意义。当然MSWD十分大时,则需要慎重对待测年结果。除此之外,更要结合地质背景,对所得结果进行检验。
5 讨论
在同位素地质年代学研究中,最小二乘法直线拟合是一种常用的数学处理方法。虽然普通最小二乘法广为人知,但由于拟合所用数据点均为测试所得同位素比值,纵横坐标变量均存在误差甚至误差相关,而普通最小二乘法假设一个变量不存在误差的前提条件已经不能成立。因此,需要建立更加符合数据本身特点的拟合方法。
基于此,我们在前人研究的基础上,对最小二乘法进行了系统性地总结与研究。详细介绍了普通最小二乘法、加权普通最小二乘法、标准加权最小二乘法、标准独立加权最小二乘法、独立加权最小二乘法以及误差相关最小二乘法,给出了各自的“最小二乘”原理,以及拟合直线斜率、截距及其误差的计算方法。在将相关数学计算方法进一步完善并系统化的同时,也阐明了各种最小二乘模型之间的相互关系。误差相关最小二乘法可以看作是最一般的情形,而独立加权、标准独立加权、标准加权、普通最小二乘法则可看作是其一步步“特殊化”的情形。误差相关、独立加权这两种最小二乘法没有数值解,需要借助计算机编程后用迭代法得到其近似解,文中给出了迭代的具体算法;而前四种最小二乘法则具有数值解。
可以看出,不同的拟合模型对应于不同的假设条件,这允许根据数据本身的特点,选择合适的模型进行拟合。如对于U-Pb不一致曲线,只能选择误差相关最小二乘法,而对于Rb-Sr、Sm-Nd、K-Ar、Re-Os等时线法等,则可选用最一般形式的独立加权最小二乘法。当然,如果数据有符合标准独立加权、标准加权、(普通)最小二乘法的假设条件的,即可采用这些简化的模型,从而简化计算。这里,笔者发现对于Rb-Sr、Sm-Nd等时线法,由于87Rb/86Sr(147Sm/144Nd)的实验误差比87Sr/86Sr(143Nd/144Nd)要大许多,因此采用普通最小二乘法或加权普通最小二乘法,将数据点偏离拟合直线的原因全部归于横坐标x(87Rb/86Sr,147Sm/144Nd),或许是可以接受的。
我们进一步澄清了参数MSWD对于同位素地质年代测定结果的参考意义。理论上,在拟合直线时,应该考虑包括每个样品的采样、地质背景、方法应用及实验分析所带来的所有误差,但实际上只有实验分析误差是可定量估计的。因此,拟合过程中我们只考虑了实验分析误差。鉴于此,在所选样品尽量符合所用测年方法原理的基础上,如果实验分析误差估计准确,那么当MSWD落入其95%的概率区间内或不至于太大时,拟合结果具有较大的参考意义,但也不排除错误的测年结果存在的可能性。当MSWD过于大时,则需慎重。当然,由于地质“未知”世界的复杂性,在评价拟合结果时,也需要结合已有的地质知识进行判别。实际研究中,对于每一个数据点,更需将其看作“一个个同位素比值”,而非“一个个年龄”。
同位素年代学研究方法是建立在一定的假设基础之上的,根据地质样品本身的规律,对这些假设予以统计学修正,应该是今后发展的一个方向。这也有利于以地质学内容为素材,开拓新的方法。我们的研究对于其他自然科学及社会科学领域内,相似问题的解决也具有一定的参考意义。
6 结论
本文对最小二乘直线拟合这一同位素地质年代学中常用的统计方法进行了总结,详解了其数学原理与实现过程,实现了从普通最小二乘模型到误差相关最小二乘模型的统一。不同类型的最小二乘模型对应于不同的假设条件,研究者可据其数据特点进行选择。对于U-Pb不一致曲线,只能选择误差相关最小二乘法,而对于Rb-Sr、Sm-Nd、K-Ar、Re-Os及其它等时线,除可选用最一般形式的独立加权最小二乘法,也可据数据特点,选择标准独立加权、标准加权、普通最小二乘法等简化模型计算。在此基础上,我们进一步澄清了MSWD这一参数对拟合结果的评判意义。准确理解这些,对于我们更好地应用相关测年方法,评价测年结果的可靠性至关重要。我们的研究也可用于其他领域内相似问题的研究中。
致谢:本文完成过程中得到了北京离子探针中心宋彪研究员,中国科学院地质与地球物理研究所姜能研究员、储著银副研究员,中国地质大学(北京)诸慧燕老师、苏文博教授、高世臣教授、王翠香副教授,中国军事医学科学院张春茂、上海财经大学马馨瑞及中国地质大学(北京)甘彩虹、薛玉山、杨宽、张志强等的帮助,匿名评审人及章雨旭编辑的认真工作使本文进一步完善,在此一并表示衷心感谢。

