在问题中培养思维能力

在浙江省杭州市结束的“卡西欧杯”第八届全国初中青年数学教师优秀课观摩与评比活动中，无锡市江南中学张珉老师凭着新颖独特的教学设计、沉稳干练的教学风格和扎实全面的综合素质，赢得现场知名专家和来自全国各地数千名教师的一致肯定和赞扬，并荣获一等奖。

张老师上的课为苏科版《数学》七年级（上）“有理数和无理数”的教学内容。新修订的苏科版教材把无理数的概念前置到有理数部分之前，目的是完善数学体系，为后续涉及实数体系知识的教学提供依据。本节课先让学生感受无理数产生的现实背景和引入的必要性，然后让学生经历无理数发现的过程，感知生活中确实存在有不同于有理数的数，从而激发学生探求的欲望，最后归纳得到有理数和无理数的定义，并能清晰地判断有理数和无理数。

创设“情境型”问题，培养思维的深刻性

师：随着年龄的增长、学习的深入，我们对数的认识也在不断地更新，请同学们回忆一下，到目前为止，我们已经学过了哪些数？

生：自然数、整数、分数、正整数、负整数、正分数、负分数、小数、有限小数、无限循环小数、无限不循环小数、偶数、奇数、质数（素数）、合数、正数、负数……

师：我们已经学过了这么多数，那么这些数之间有什么关系，让我们来整理一下？

生：正整数、负整数、0、自然数、素数（质数）、合数、奇数、偶数。

（在开始记录的数的上方编号①）

师：你能把属于分数的都找出来吗？

生：正分数、负分数、有限小数、无限循环小数、带分数（在开始记录的数的上方编号②）。

师：剩下还有一些数，它们是整数吗？是分数吗？

生：不是整数，也不是分数。

师：如果说到“正数、负数”，那么它们与整数是什么关系？

生：正数里有整数，负数里也有整数。

师：正数中有一部分数是整数，就是正整数，负数中有一部分数是整数，就是负整数，还有什么整数？

生：0。

师：小数有哪些呢？

生：有限小数、无限循环小数。

师：有限小数可以化为分数，无限循环小数可以化为分数。还有没有其他的小数呢？

生：π、0.3142537…

师：它是整数吗？是分数吗？

生：都不是。

（课件展示π）

师：借助电脑计算可得到π的一个结果，但是还没有写完，其实也写不完，所以最后用了省略号。请同学们观察，它是怎样的一个小数？（说不出无限，提示省略号是什么含义）是一个循环小数吗？事实上是一个无限不循环小数。

…………

《数学课程标准》指出：“要增强学生发现问题和提出问题的能力，要重视学生的问题意识以及解决问题综合能力的培养。”在本教学片段中，张老师通过与学生一起回顾所学过的数，帮助学生认识到：以前学过的数中绝大多数是整数和分数，绝大多数小数也都可以转化为分数或整数。但也有极个别的数没法化成分数或整数，这些数拥有共同的特征：都是一个无限小数，而且小数点后的数，其排列是“无循环规律”。张老师通过这样的教学过程，揭示了无理数的客观存在及其本质属性——无限不循环的小数。

建立“活动型”问题，培养思维的探究性

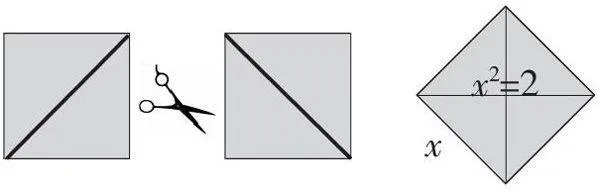
师：请同学们拿出准备好的两个边长为1cm的小正方形和剪刀，将小正方形沿着图中对角线剪开，设法重新拼成一个大正方形。大家动手试一试剪剪看。

（学生动手操作）

师：经过同学们的努力，基本都完成任务了，请两位学生把自己拼的图在黑板上展示。

师：你们知道这个大正方形的面积是多少吗？为什么？

生：它的面积为2cm2，因为它是由两个面积为1cm2的小正方形拼成的。

师：知道了这个图形的面积是2cm2，你还想知道它的一些什么信息呢？

生：边长。

师：你能不能求出边长？

生：……

学生在小学阶段对自然数、分数或小数等有了初步的认识，进入初中后，接触到了负数，学生所认识的“数”有了进一步的扩充，同时也知道了整数和分数的分类。但学生在学习“无理数”概念时可能会存在困难或疑惑，为此，张老师在教学中设计了操作活动——把两个面积为1cm2的正方形剪拼成面积为2cm2的大正方形，再提出这个大正方形“你能不能求出边长”的问题，引导学生探索，这样既能使学生确认无理数的存在，又能顺理成章地导出无理数的概念。通过拼图，让学生感受到现实世界中真真切切存在着“a2=2”这样的实际例子，揭示了研究无理数的必要性和现实性。同时让学生在动手操作中发现问题、提出问题，通过分析、类比、归纳、讨论、交流等形式解决问题，自然生成概念，形成认知。

巩固“再生型”问题，培养思维的严密性

师：把下列各数分别填入相应的大括号内：

-0.5，-6，2.5，0，+3，-0.333，

-1.41421356……，2005，3.141，85%，0.3030030003……，，π。

生：有理数集合有：{-0.5，-6，2.5，0，+3，-0.333，2005，3.141，85%，，……}；无理数集合有：{-1.41421356……，0.30300 30003……，π……}。

师：分数都是有理数吗？

生1：不一定，如，计算器计算显示的结果是3.142857143，但好像是无限不循环小数，也就是无理数。

生2：不一定，如就是无理数。

在本教学片段中，张老师引导学生理解有理数的意义，了解无理数的概念，判断一个数是有理数还是无理数。在教学过程中，张老师设置大量教学活动，让学生动手动脑，积极参与教学活动，体现了“数学教学主要是数学活动的教学”这一教育新理念。

综观整节课，张老师的教学是以学生的“学”为出发点进行设置的，层层递进，使学生主动地获取知识，并在获得知识的过程中感受转化、归纳、特殊与一般等数学思想，促使思维相互碰撞，进一步激发思维的灵感以迸发创造的火花。教师对本课的重点（理解有理数与无理数的概念）和难点（无理数概念的理解）把握得非常准确。在拼图中，教师通过“知道了这个图形面积是2cm2的正方形，你还想知道它的一些什么信息呢”这样一个简单设问，展现了数学家的思考方式，培养学生学习“数学地思考问题”；在探索过程中，通过实践、操作、探索、思考、归纳，展现了数学研究的方式，同时渗透了数学中的一种重要思想——逼近思想。

在教学中，张老师能处处以学生为主体，引导学生不断地试验、操作、探索，渐渐走向真理。本节课注重活动与探究相结合，讨论与归纳相结合，思维训练与能力提升相结合，以知识点形成知识链，再结合已有知识形成知识网络，很好地完成了本节课的教学目标。整个教学过程重在学生的感知、感悟、数学思想方法的渗透，培养学生学习数学的方法，培养学生的实践意识和探索精神，是一堂难得的好课（作者单位：江西省吉安市神岗山学校）

□责任编辑 周瑜芽

E-mail：jxjyzyy@163.com