基于零售商不同风险偏好的三级供应链利润模型
葛娜, 汪传旭, 姚漫
(上海海事大学 经济管理学院,上海 201306)
0 引 言
供应链环境中,存在各种不确定因素,如自然灾害、供应商供应产品的及时性、合作竞争伙伴是否中断合作关系等,这促使决策者在作决策时往往考虑其中的风险因素以享有最大效益.近几年,供应链风险问题已经引起众多国内外学者和企业管理层的关注[1-2].RICE等[3]定义6种基本的供应链风险中断模型,如供应中断、运输设施中断等.GOH等[4]考虑与供应、需求、汇率和失效相关的一组风险,构建全球多级供应链网络优化随机模型,实现利润最大化和风险最小化的目标.AZARON等[5]提出不确定环境下供应链网络设计问题的多目标随机规划模型,需求、供应、处理、运输、缺货等都被考虑为不确定参数.AGRAWAL等[6]考虑一个具有风险厌恶特性的零售商,当销售价格分别影响需求规模和需求分布时,具有风险厌恶特性的零售商对销售价格和订货数量具有不同选择.EECKHOUDT等[7]和CACHON等[8]针对具有单个风险厌恶特性的合作伙伴的供应链协作方式进行研究.ANASTASIOS等[9]在一个双源供应链网络中,考虑决策者为风险厌恶和风险中性两种情况,建立库存模型.秦娟娟等[10]提出在寄存契约下,供应链中供应商的生产量及各成员的利润均为供应商损失规避程度的减函数的结论.鲁凯[11]利用委托-代理理论,分别研究供应商和销售商在具有相同风险偏好和不同风险偏好下供应商对销售商的最优激励机制的设计问题.杨道箭等[12]在具有策略行为与风险偏好的顾客群体所组成的供应链中,研究供应链利润分享契约问题,得出销售商的利润随着顾客风险偏好程度的增加而减少的结论.杨德礼等[13]研究供应商和零售商在不同的风险偏好组合下的供应链协作方式并建立相应的供应链协作模型.周宝刚等[14]将供应商产品价格、风险等级、供应能力和零售商需求考虑为不确定性因素,建立基于风险偏好的两级供应链集成优化模型.综上所述,现有文献在考虑供应链风险时,很少同时考虑决策者具有3种不同风险偏好的情况,也很少会考虑当供应链发生中断时产品转运的情况.此外,现在关于风险度量的文献大多基于供应链中某一方利润最大化,很少考虑使供应链总体利润最大化.与现有文献相比,本文创新点主要体现为:(1)在制造商为风险中性的条件下,考虑供应发生中断时,制造商之间可以发生转运的情况;(2)同时考虑零售商存在风险偏好、风险中性和风险厌恶3种风险偏好,分析3种风险偏好对订单量和供应链各方利润及总利润的影响.
1 问题描述与基本模型
1.1 问题描述

图1 模型示意图
如图1所示,在由1个供应商、2个制造商和1个零售商组成的三级供应链中,零售商向制造商1和2提交订单.由于供应链中存在多样风险,制造商可能发生供应中断.本文假设:(1)制造商1可能发生供应中断,制造商2不会发生供应中断.(2)在制造商1未发生供应中断时,供应商向制造商提供充足的原材料;当制造商1发生供应中断时,供应商立即停止向制造商1提供原材料,只对制造商2提供原材料.(3)在供应链中,根据零售商和制造商的利润总和最大化分配订单量和转运量.制造商1发生供应中断的概率为p,中断发生时,制造商1向零售商提供的产品数量为0,即不提供产品.为了使供应链总利润最大,制造商2决策是否将自己多余的产品转运给制造商1.
1.2 参数设置

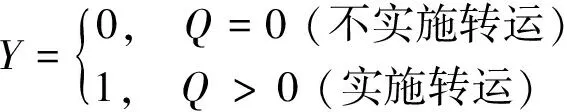
1.3 基本模型
首先考虑在零售商为风险中性情形下的基本模型.零售商的利润包括两部分:一部分为制造商1不发生供应中断时的利润,另一部分为制造商1发生供应中断时的利润.
制造商1不发生供应中断时零售商的利润
(1)
制造商1发生供应中断时零售商的利润
(2)
零售商的总利润
Πre=(1-p)Πre(Q1,Q2)+pΠre(YQ,Q2)
(3)
式(1)和(2)可进一步分别表示为
制造商的利润

(6)
2 零售商为非风险中性的决策模型
2.1 VaR和CVaR的概念
在现实中,每个决策者的风险偏好不可能都是风险中性.在决策过程中,往往会考虑决策者的不同风险偏好,即考虑风险厌恶、风险中性和风险偏好对供应链总利润的影响.风险值(Value at Risk,VaR)和条件风险值(Conditional Value at Risk,CVaR)作为风险管理中应用广泛的风险度量准则,便于计算,可以作为解决此类问题的工具.
设z=f(x,y)为损失函数,ψ(x,ζ)=P(y|f(x,y)≤ζ),即ψ(x,ζ)是z=f(x,y)的分布函数[14].
定义1:α-VVaR.ζα(x)=min(ζ|ψ(x,ζ)≥α|).α-VVaR的直观意义为损失函数z=f(x,y)超过α-VVaR的概率是1-α.α为利润截断水平,α越大,决策者的风险厌恶程度就越明显.

由于α-VCVaR较难计算,ROCKAFELLAR等[15]提出一种转化方法,可以将α-VCVaR快速方便地计算出来.引入函数
式中:(f(x,y)-ζ)+=max(0,f(x,y)-ζ).
GOTOH等[16]在2007年将利润的负值定义为净损失,即某供应商的利润为Π,则该供应商的净损失为-Π.零售商的α-VCVaR函数
(7)
2.2 决策模型
从VaR和CVaR的定义不难看出,VaR和CVaR过多关注利润低于给定水平平均利润的情况.在现实中,市场随机需求等随机因素的存在使各级决策者获得的利润具有随机性,最终利润可能高于或低于决策者心中的安全利润.具有不同风险偏好的决策者对高盈利和低盈利的关注度也不同.
本文用决策者对盈利水平高低的不同关注程度来表现不同的风险偏好,若决策者为风险偏好,则更关注于高盈利,即喜欢追求可能出现的高利润,而不仅仅是安全利润;若决策者为风险厌恶,其对安全利润的关注程度要远远高于对高风险高利润的关注程度;若决策者为风险中性,其对高盈利和低盈利同样关注.引入β表示决策者区分高盈利和低盈利的截断水平,随机利润由高到低排列,前β%为高盈利,后(1-β)%为低盈利.β取值大小由决策者对风险偏好的程度决定.
由α-VVaR和α-VCVaR理论得出α为截断水平β.若决策者为风险厌恶,α值较大,即有α%的可能性高于心目中所期望收益时的利润,才属于高盈利.
设零售商在α处所对应的安全利润为Πα,re,根据以上论述可知,Πα,re即为-(α-VVaR)re.用E1和E2分别表示高盈利和低盈利的期望值,λE1+(1-λ)E2表示决策者对于风险不同偏好的目标函数.若决策者为风险偏好, 则λ>0.5;若决策者为风险厌恶,则λ<0.5;若决策者为风险中性,则λ=0.5.E1和E2的表达式:
(8)
(9)
引入函数G(Q1,Q2,ζre)=λE1+(1-λ)E2,对于零售商而言,无论是何种风险偏好,其最终目标都是最大化G(Q),同时使供应链总利润最大.当λ=0.5时,此时零售商决策者的风险态度为中性,G(Q)=Πre.当λ≠0.5时,根据式(3)可将Πre分为3个不同的区间.由第2.1节得,零售商净损失同样分为3个不同的区间.根据净损失的3种不同区间分情况对G(Q1,Q2,ζre)=λE1+(1-λ)E2进行求解.



(10)

(11)

(12)
求解可得出最优解.

为了便于计算,将零售商具有风险偏好的供应链总利润作为目标函数,式(10)~(12)作为约束条件建立目标规划函数:
(13)

3 算例分析
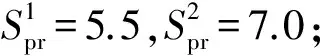
3.1 零售商为风险中性
零售商为风险中性,即λ=0.5时,G(Q)=Πre,此时零售商和制造商的总利润不随零售商利润截断水平α变化而变化,结果是一致的.求解结果为Q1=179,Q2=879,YQ=0,零售商的总利润Πre=361,制造商的总利润Πpr=4 824,供应链总利润为5 185.
3.2 零售商为非风险中性
当零售商为风险偏好或风险厌恶时,由G(Q1,Q2,ζre)=λE1+(1-λ)E2得出,零售商的利润因λ和α的不同而不同;相应地,制造商的利润也发生变化,进而影响供应链总利润.α取不同数值时,不同λ下的订单情况见表1.
3.3 比较分析
3.3.1λ和α对订单量的影响
给定零售商α,改变λ可得:当λ逐渐增大时,零售商向制造商1提出的订单量Q1逐渐减少,零售商向制造商2提出的订单量Q2普遍增加,由制造商决策的转运量Q逐渐减少.当λ较小时,零售商关注低盈利更多.由于制造商1的产品价格小于制造商2的产品价格,同时产品的转运价格高于制造商1的产品价格,零售商向制造商1提出较多的订单.具有较低风险偏好的零售商在可能发生供应中断的情况下,尽可能降低自身订购成本,增加自身利润.

表1 α取不同数值时不同λ下的订单情况
随着λ的增大,零售商对于风险持偏好态度,更多地追求高盈利,此时逐渐增大制造商2的订单量,减少转运量和制造商1的订单量.当制造商1发生供应中断时,制造商2从供应链总利润最大化角度出发决策是否将自己多余产品中转给制造商1,无论是否发生中转,零售商都最大可能满足市场需求.通过算例分析,当λ增大时,零售商的订购成本虽然增加,但其自身利润也不断增加,供应链总利润也随着增加,满足具有风险偏好的零售商对于高盈利的追求.当α≤0.30时,这种变化趋势尤为显著.
3.3.2λ和α对供应链各方利润的影响
给定零售商α,改变λ可发现:当λ逐渐增大时,制造商和零售商的利润以及供应链总利润也随之增大.不难发现,制造商的利润之和普遍大于零售商的利润.这是由于在供应中断时,由制造商自行决策是否进行产品转运,达到供应链的最大利润,因而制造商具有先动优势,在供应链利润分配中享有大部分的利润.
比较λ相同而α不同时的各方利润.给定零售商λ,改变α可发现:当α逐渐增大时,零售商利润逐渐增加,但是制造商利润并非逐渐增加,由于制造商的先动优势,进而影响供应链总利润,使供应链总利润呈现先增加后减少的趋势.制造商和零售商都尽可能使供应链总利润变大,通过有效的收益分配方案,如Shapely值法,使自身利润增加,便于以后供应链合作.
当λ取相同值时,比较零售商期望损失ζre随α变化的情况可得,随着α的逐渐增大,ζre的绝对值逐渐减小.如前所述,α变大,说明零售商的利润增加,ζre绝对值变小.
将表1中的利润数据与零售商决策者为风险中性时各个利润比较可得,当零售商具有一定的λ和α时,零售商利润、制造商利润以及供应链总利润均大于零售商决策者为风险中性时的各个利润.这说明在供应链合作中,具有风险偏好的某一方可以增大供应链总利润,各方利润也会增加.
4 结 论
研究由1个供应商、2个制造商和1个零售商组成的三级供应链中,制造商可能发生供应中断,零售商存在风险偏好、风险中性和风险厌恶等3种不同风险偏好对供应链订单量以及供应链总利润的影响.并且进一步考虑到,若制造商发生供应中断,允许发生转运.引入与VaR和CVaR相关的风险度量函数,详细表述零售商决策者的不同风险偏好,建立相应的数学模型,提出供应链总利润目标规划函数.最后,通过算例分析验证模型的有效性,得出当零售商具有一定风险偏好时可以增加供应链总利润,进而增加供应链各成员利润.在以后的研究中,可以同时考虑制造商的风险偏好,进而得出制造商和零售商合作的最佳风险偏好组合.
参考文献:
[1] OKE A, GOPALAKRISHNAN M. Managing disruption in supply chain: a case study of a retail supply chain[J]. Production Econ, 2008, 118(1): 168-174.
[2] 郑平, 何雪君. 物流外包业务的风险矩阵模型[J]. 上海海事大学学报, 2011, 32(1): 80-85.
[3] RICE J B Jr, CANIATO F. Supply chain response to terrorism: creating resilient and secure supply chains, interim report of progress and learnings[R]. MIT Center for Transportation & Logistics, 2003-08-08.
[4] GOH M, LIM J Y S, MENG F. A stochastic model for risk management in global chain networks[J]. Eur J Operational Res, 2007, 182(1): 164-173.
[5] AZARON A, BROWN K N, TARIM S A,etal. A multi-objective stochastic programming approach for supply chain design considering risk[J]. Production Econ, 2008, 116(1): 129-138.
[6] AGRAWAL V, SESHADRI S. Impact of uncertainty and risk aversion on price and order quantity in the newsvendor problem[J]. Manufacturing Serv Operation Manage, 2000, 2(4): 410-423.
[7] EECKHOUDT L, GOLLIER C, SCHLESINGER H. The risk averse (and prudent) newsboy[J]. Manage Sci, 1995, 41(5): 786-794.
[8] CACHON G, FISHER M. Supply chain inventory management and the value of shared information[J]. Manage Sci, 2000, 46(8): 1032-1048.
[9] ANASTASIOS X, DIMITRIOS V, ELEFTHERIOS I. Optimal newsvendor policies for dual-sourcing supply chain: a disruption risk management framework[J]. Computers & Operations Res, 2012, 39(4): 350-357.
[10] 秦娟娟, 赵道致. 风险偏好信息非对称下的供应链寄存契约研究[J]. 管理学报, 2011, 8(2): 284-288.
[11] 鲁凯. 供应商对不同风险偏好的销售商激励机制研究[J]. 物流技术, 2007, 26(11): 110-113.
[12] 杨道箭, 齐二石, 魏峰. 顾客策略行为与风险偏好下供应链利润分享[J]. 管理科学学报, 2011, 14(12): 50-59.
[13] 杨德礼, 郭琼. 基于不同风险偏好组合的供应链协作方式的研究[J]. 管理科学, 2005, 18(5): 7-10.
[14] 周宝刚, 关志民, 杨锡怀. 基于风险偏好的两级供应链集成优化[J]. 工业工程与管理, 2010, 15(6): 21-25.
[15] ROCKAFELLAR R T, URYASEV S. Conditional value-at-risk for general loss distribution[J]. J Banking & Finance, 2002, 26(7): 1443-1471.
[16] GOTOH J K, TAKANO Y. Newsvendor solutions via conditional value-at-risk minimization[J]. Eur J Operational Res, 2007, 179(1): 80-96.
- 上海海事大学学报的其它文章
- 多负载非接触电能传输系统传输效率方程
- 基于神经网络的集装箱码头泊位分配聚类分析

