基于局部约束线性编码的单帧和多帧图像超分辨率重建
卜莎莎,章毓晋
(清华大学电子工程系,北京100084)
图像采集时,受到采样设备分辨率不高的限制及环境中多种因素的干扰,获取的图像不够清晰,蕴含丰富信息的细节模糊或缺失,导致图像分辨率降低。低分辨率的图像难以满足人们在后续的图像处理和识别等方面的需要,给目标的定位和识别、图像信息内容的获取等带来诸多不便。超分辨率技术可以充分挖掘图像的潜在信息,利用图像先验知识,得到高质量的图像,在卫星侦察、视频监控等多个领域得到广泛应用。
超分辨率的技术从20世纪80年代以来得到了迅猛的发展,目前常用的算法有凸集投影法[1]、最大后验概率法[2,3]、迭代反投影法[4]等。近年来基于学习的超分辨率重建算法也逐步发展起来,最近文献[5]提出了一种基于稀疏表示的超分辨率重建算法,取得了不错的效果。笔者在稀疏表示算法[5]的基础上进行了改进,提出一种基于局部约束线性编码(LLC:Locality-constrained Linear Coding)[6]的超分辨率重建方法。实验表明,改进后的算法图像重建质量更高,运算速度更快,效果更好。
1 基于稀疏表示的重建算法
稀疏表示算法[5]的基本思想是:基于成对的高分辨率图像块和与之相应的低分辨率图像块进行词典训练,得到成对的高分辨率词典Dh和低分辨率词典Dl。然后根据得到的低分辨词典Dl对输入的低分辨率图像进行编码,再依据该编码和高分辨率词典s重建得到高分辨率图像。算法大致可分为3个步骤:词典训练,稀疏编码,图像重建。
1.1 词典训练
令Dh为高分辨率词典,大小为N×K,Dl为低分辨率词典,大小为M×K。二者都是过完备的词典,即K>N且K>M,词典的过完备性为稀疏编码提供了保证。词典训练的目标为根据训练集中的一系列成对的高分辨率图像块和低分辨率图像块,结合稀疏表示的算法原理,得到成对词典Dh和Dl。联合词典训练方法如(1)所示。
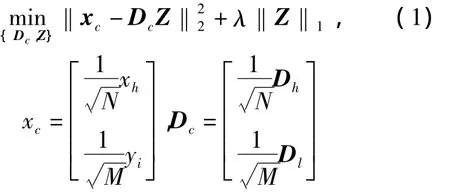
其中xh为高分辨率图像块,yl为相应的由低分辨率图像得到的高分辨率图像块,N和M分别为高分辨率图像块和低分辨率图像块转换成列向量后的维数。式(1)中需要同时对Dc及Z进行优化,实际求解过程中可采用迭代算法,固定其中一项,对另一项进行求解,通过反复迭代可求得满足条件的解。
1.2 稀疏编码
将输入的低分辨率图像划分成固定大小的小块,每个小块之间有一定重叠,然后对划分后的小块y进行稀疏编码:
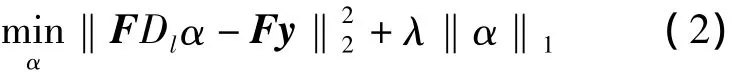
其中F为特征提取矩阵,Dl为低分辨率词典,y为低分辨率图像块,为根据Dl得到的y的编码。L1范数保证了编码的稀疏性,拉格朗日乘子λ用于在编码的准确性和系数性中取得平衡。
为同时考虑到低分辨率图像和重建得到的高分辨率图像编码的准确性和稀疏性,可采用如下公式对二者进行联合编码:

其中β用于在高分辨率词典和低分辨率词典之间的取得折中,P用于提取当前块和已经重建好的高分辨率图像块之间的重叠区域,以保证重建的连续性,x为待重建的高分辨率图像块
1.3 图像重建
根据编码得到的系数ω和高分辨率词典Dh,利用式(4)可重建得到高分辨率图像块,这些高分辨率图像块再拼接到一起,即可得到一个初步的高分辨率图像X0。

再根据输入的低分辨率图像Y利用图像降质模型,通过梯度下降的方法寻找与X0最接近的图像X,即可得到恢复后的高分辨率图像X*。求解方法如下
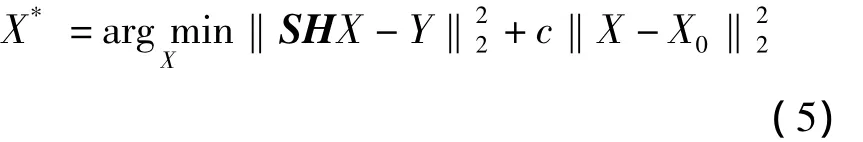
其中S为降采样矩阵,H为模糊矩阵。
2 LLC编码
LLC编码侧重于局部的约束,而非稀疏性,根据文献[6],局部性可以带来稀疏性,但稀疏性未必满足局部性。从这方面而言,局部性约束比稀疏性约束更为重要。LLC的编码满足下式的约束:

其中xi为待编码的的向量,B为词典,ci为经过LLC得到的编码。di为不同编码的权重,用于权衡编码中每个元素和词典B中相应列的关系。·代表向量元素维度的相乘。di可如下计算:
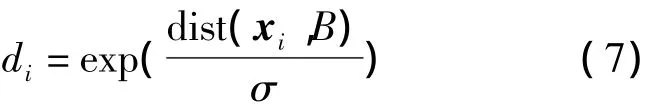
其中σ为可调整的参数,用于控制di的大小,dist(xi,B)为矢量,每个元素代表向量xi与词典B中每列向量的欧氏距离。
因加入局部性的约束,LLC编码相对于稀疏编码[5](SC:Sparse Coding)而言更为平滑。稀疏编码[5]时,为满足编码的稀疏性,相似的像素块得到的结果有可能差异较大,而词典的过完备性更加剧了这一差异。LLC编码能保证相似的像素块得到相近的编码,从而保证重建出的像素块的相似性,保证局部平滑。
稀疏编码[5]时需要采取优化算法进行迭代,带来较高的计算量,而LLC算法有解析解,能够降低运算消耗,加快运算速度。
3 基于LLC的超分辨率重建算法
笔者在稀疏表示算法的基础上进行了改进,利用LLC的方法对图像块进行编码,实现超分辨率重建。算法流程如下。
3.1 图像分块
无论在词典训练阶段还是在超分辨重建阶段都需要对图像进行分块,适当的分块可降低计算复杂度,加快运算速度,提高重建的精度,保证图像重建的效果。笔者算法首先将输入图像按照从上到下、从左到右的顺序进行分割,划分成3×3的小块,同行邻近的像素块之间有一列重叠,同列邻近像素块之间有一行重叠,以保证像素块之间的连续性,防止像素块边缘因不连续而导致的突变。
3.2 联合词典训练
为加强词典训练中高分辨率词典和低分辨率词典之间的相关性,训练集中的低分辨率图像由高分辨率图像经过亚采样和模糊后得到。为保证词典训练的效果,将低分辨率图像再经升采样之后,和高分辨率图像进行联合训练,这样有利于更好地找到二者之间的对应关系。
超分辨率重建更注重于恢复图像的高频细节,因而在对升采样的低分辨率图像进行分块处理之前,先通过特征提取矩阵得到高频分量,然后对高频分量之间的对应关系进行训练,得到成对的词典Dh和Dl。特征提取算子可如下设计[5]:
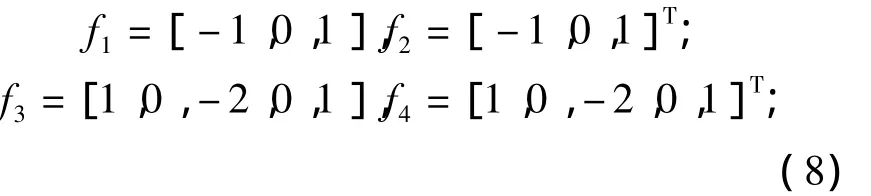
其中f1和f3用于提取行的特征,f2和f4用于提取列的特征。将特征提取算子与待训练的图像进行卷积,得到4幅保留了边缘信息的特征图像,对这4幅图像分块,将对应的图像块整合成一个矢量,即可得到用于词典训练的向量。
提取完特征并分块后的图像按照式(1)进行词典训练,直至满足收敛条件。
3.3 使用LLC对图像编码
词典训练完毕之后即开始图像的编码过程,图像编码前也要经过和词典训练相似的预处理过程。对于一幅输入的低分辨率图像,同样依据式(8),进行特征提取,得到4幅图像。然后将其按照3.1节中提到的方法进行图像分块处理,将4幅图像中对应的小块整合成一个向量yi,按照训练得到的低分辨率词典Dl进行LLC编码,具体计算过程如下:
1)计算y和词典Dl每列向量之间的距离,进而得到编码元素的权重di,类比式(7),对应的计算如下
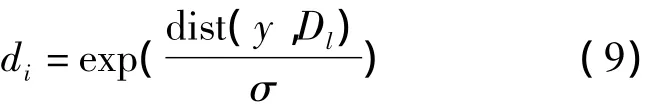
2)根据已经得到的di按照下式计算LLC编码后的系数αi:

3.4 超分辨率重建
根据上面得到的系数αi和训练得到的高分辨率词典Dh,即可重建高分辨率图像块xi:

高分辨率图像块xi按照从左到右,从上到下的顺序拼接起来,同时考虑到低分辨率图像分块时的混叠,即可得到初步重建后的高分辨率图像X0。
3.5 全局约束与恢复
鉴于上述重建考虑的都是局部约束条件,每个重建的图像块都是局部最优,但不一定能满足全局最优的条件。初步重建的图像X0和得到初步的高分辨图像X0之后,还需对其进行全局的处理和恢复。
对X0采取后向投影的方法:将X0向输入低分辨率图像Y上投影,得到投影后的图像Y+,再将Y+和Y的差值Y映射到高分辨率空间,叠加到X0上。重复上述过程,迭代一定次数后可得到加入全局约束后恢复得到的图像。全局约束的算法还有很多,可根据实际自主选择。
4 多帧图像超分辨率重建
将基于LLC编码的单帧超分辨率重建算法扩展到多帧算法,采用和式(2)类似的方法,将多帧图像的数据整合到同一个编码公式里,对整体优化,求得最优解,利用图像序列之间的互补信息,提高图像超分辨率重建的质量。
首先对输入的多帧低分辨率图像进行运动估计和帧间配准[7],然后对配准好的多帧超分辨率图像进行多帧超分辨率重建,编码式如下:

其中αk,l为中心点位于(k,l)处的图像块经稀疏编码后的系数,F为特征提取矩阵,Dl为低分辨率词典,Ri,j为图像块提取算子,用于从低分辨率图像Yt中提取中心位于(i,j)的图像块。ω为权重系数,用于控制各帧图像对于最终编码系数的约束程度。
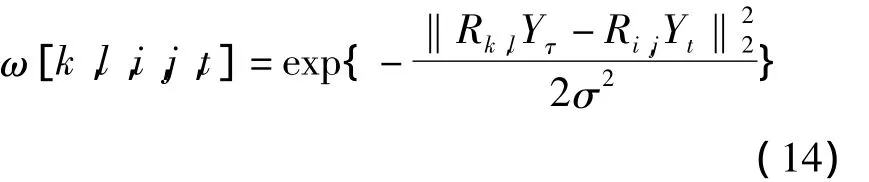
得到编码系数后的重建及全局恢复步骤同第3节,可得到经过多帧重建的高分辨率图像。
5 实验结果
为更好地对比算法性能,笔者从重建效果、运算速度、噪声影响等多个方面对超分辨率重建的结果进行展示和分析,并展示了多帧重建图像的对比结果。
文献[5]中已将其提出的算法和后向投影(Back Projection)[8]、邻近嵌入(Neighborhood Embedding)等多种算法进行了比较,取得不错的效果。笔者算法只和其中效果最好的文献[5]算法及常见的Matlab中的bicubic插值算法进行对比。
5.1 重建效果
将图像块统一划分为3×3的小块,每块之间重叠按照3.1节所示方法,采用1024维的词典进行超分辨率重建,放大倍数为3,全局恢复时采用后向投影的算法,得到的图像重建效果如下。

图1 超分辨重建效果图Fig.1 Super-resolution effect image
图1中PSNR依次为:26.8270 dB,28.6990 dB,29.5986 dB,29.6842 dB。笔者算法相对于文献[5]的方法提高了0.0852 dB。其中帽子和肩膀边缘效果尤其明显,振铃现象得到缓解。
几种不同方法重建得到的PSNR值可参见表1,其相应的低分辨率图像见图2。

表1 不同方法重建图像的PSNR值Table 1 PSNR of differentmethods

图2 实验用低分辨率图像Fig.2 Low resolution images used for experiments
实验结果表明,该算法相对于文献[5]方法的PSNR值平均提高了0.0783 dB,重建效果有所提高。
5.2 抗噪性能
为进一步对比不同算法在抗噪声方面的性能,该实验中对原始图像加入不同种类,不同大小噪声,然后对其进行超分辨率重建,对比各算法在抗噪性能上的优缺点。为方便起见,只选取图1进行了对比。
如图3左上图像所示,原始输入低分辨率图像被叠加了均值为0,方差σ为0.001的高斯加性白噪声,需要指出的是这里的噪声产生通过Matlab中的imnoise函数产生,为σ相对于图像归一化之后的方差。

图3 加入噪声后超分辨率重建图像Fig.3 Super-resolution reconstruction of noisy image
按照同4.1节相同的参数设置对图像进行超分辨率重建,得到4种方法的重建效果如图3PSNR值依次为:26.4090 dB,28.0557 dB,28.8086 dB,28.8966 dB。
将上述结果和图1中不加噪声的结果进行对比,为便于观察,将结果重新写于表2其余噪声对图像重建的影响也参考表2。

表2 不同方法的抗噪性能Tab.2 Robustness to noise of differentmethods
通过表2中各个算法的抗噪性能对比可以发现,随着噪声强度的增大,3种算法的重建效果均有所下降,但笔者算法的图象重建峰值信噪比(PSNR)高于其他算法。实验结果表明,笔者算法的抗噪性能优于其他两种算法,能够抵抗一定程度的噪声,提高图像分辨率。
5.3 运算速度
在第3章中提到,LLC相比于稀疏编码的方法具有更快的运算速度,能够缩短运算时间,笔者通过实验结果的统计和对比证实了这一观点。输入低分辨率图像如图1所示,两种方法参数设置同4.1节,得到的运算速度对比在表3展示。

表3 运算速度对比Table 3 Computation time of two methods
通过上述实验结果的对比,可发现对同一幅图像进行超分辨率重建,笔者方法的运算速度明显高于文献[5],且随着图像的尺寸逐渐增大,笔者方法的优越性越来越明显。实验结果进一步验证了LLC方法在提高运算速度方面的优越性。
5.4 多帧图像重建结果对比
该实验中采用4幅图像进行超分辨率重建,水平方向和竖直方向的放大倍数均为3,帧间配准时采用8×8的图像块进行运动估计,图像重建时分成3×3的小块,块之间重叠如3.1节设置,得到超分辨率重建对比的结果如下所示。
图4是用于重建的低分辨率视频序列中的一帧,选取4帧视频图像进行重建,得到的结果如图5。从上到下依次为单帧稀疏表示(SR:Sparse Representation)的重建结果,多帧SR重建,第3章所示算法即单帧LLC重建,第4章所示算法即多帧LLC重建。每行中显示了同一种方法对于视频序列中的相邻3帧的重建结果。平均梯度值如表3所示。

图4 低分辨率图像Fig.4 low-resolution im age

图5 多帧超分辨率重建后图像Fig.5 M ulti-frame super-resolution image reconstruction

表4 不同方法重建后的平均梯度值Table 4 Average gradient of differentmethods
从平均梯度值数据上可看出,多帧LLC重建效果明显好于其他算法,图像细节信息得到增强。单帧LLC算法也要好于单帧SR算法[5]。
从视觉效果上看,多帧LLC图像中字母和竖线的重建效果其他3幅图像,轮廓明显清晰,说明多帧LLC重建可以增强图像的边缘和细节信息,提高分辨率。
就LLC和SR[5]两种算法比较而言,LLC图像比SR图像的边缘振铃现象要好,SR图像中央的数字200和250难以分辨清楚,而LLC重建图像中可清晰分辨出这两个数字,分辨率明显提升。
上述对比表明,由于利用了多帧信息,多帧LLC算法的重建效果好于单帧LLC算法,图像细节进一步加强。同时也进一步证明了LLC算法相对于SR算法[5]的优越性。
综上,笔者方法相比于文献[5]的方法,在重建效果、抗噪性能及运算速度上均取得了不错的效果,推广到多帧图像超分辨率重建时图像质量进一步提高,在图像超分辨率重建方面具有一定的优势。
6 结语
笔者提出一种改进的基于局部约束线性编码(LLC)的图像超分辨率重建方法。实验结果表明,相比于稀疏表示的算法[5],笔者算法能够提高重建图像的峰值信噪比(PSNR),抵抗噪声影响,加快运算速度,推广到多帧重建质量进一步提高,取得了不错的重建效果。
[1]Galbraith A E,Theiler J,Thome K J,et al.Resolution enhancement ofmulti-look imagery for themultispectral thermal imager[J].IEEE Trans.Geoscience&Remote Sensing,2005,43(9):1964-1977.
[2]Schulz R R,Stevenson R L.A bayesian approach to image expansion for improved definition[J].IEEE Trans. Image Processing,1994,3(3):233-242.
[3]Chantas G K,Galatsanos N P,Woods N A.Super-resolution based on fast registration and maximum a posteriori reconstruction[J].IEEE Trans.Image Processing,2007,16(7):1821-1830.
[4]Ben-ezra M,Zomet A,Nayar S K.Video Super-resolution using controlled subpixel detector shifts[J].IEEE Trans.Pattern Analysis&Machine Intelligence,2005,27(6):977-987.
[5]Yang JC,Wright J,Huang T S,et al.Image super-resolution via sparse representation[J].IEEE Transactions on Image Processing,2010,9(11):2861-2873.
[6]Wang J J,Yang JC,Yu K,et al.Locality-constrained linear coding for image classification[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR).2010:3360-3367.
[7]孙宁宁.基于序列图像的超分辨率重建算法研究[D].郑州:河南工业大学,2010.
Sun Ning-ning.Super-resolution reconstruction algorithm based on image scquence[D].Zhengzhou:Henan University of Technology,2010.
[8]Irani M,Peleg S.Motion analysis for image enhancement:resolution,occlusion and transparency[J].Journal of Visual Communication and Image Representation,1993,4(4):324-335.

