四元数在均匀圆形矢量传感器阵列信号参数估计中的应用
康晓涛,王志洋,康博宇,李静静,石要武
(1.吉林大学通信工程学院,长春130022;2.上海工程技术大学管理学院,上海201620)
矢量传感器阵列能同时获取并感应到入射电磁信号的全部电场信息和极化信息,因而比传统标量传感器阵列抗干扰能力更强,检测能力更稳健,空间分辨力也更高。矢量传感器阵列因其信息获取能力强而成为国内外学者竞相研究的热点[1-3],并被广泛应用。传统长矢量模型是基于复数理论的,受复数数学结构的限制只简单的将所有分量的输出数据排列成一个长矢量,而没有考虑各分量之间的正交关系,破坏了各分量之间固有的正交结构,很大程度上降低了矢量传感器的优越性能。四元素理论特有的四维超复数正交结构能够保持矢量信号各分量之间固有的正交结构,为解决上述问题提供了一个有效方便的数学工具。四元素广泛应用于各个领域[4-7],在矢量传感器阵列信号处理领域中主要是对极化信号的波达方向和极化参数等方面进行估计[8-11]。
本文通过构造基于四元数的均匀圆形电磁矢量传感器阵列的信号接收模型,对电磁波信号入射到阵列的方向角和极化信息等参量进行联合估计。四元数的四维超复数结构是复数的扩充和发展,因而可以说复数是四元数的一个特例。四元数因其不满足乘法交换律,因而其矢量正交性比复数有更多的约束条件,四元数的正交结构能够保持矢量传感器各分量固有的正交性,而正交性恰是信号处理中最有效且常用的手段之一。因此四元数的矢量正交性是四元数有别于复数的一个突出特点。仿真实验验证了方法的有效性。
1 数学模型
采用极化均匀圆阵(UCA)作为信号模型,它由N个均匀分布在半径为R的圆周上特性一致的紧凑电磁矢量传感器构成,如图1所示。
考虑k≤N个窄带,不相关且完全极化的电磁波以一定方向从远场入射到上述信号模型。
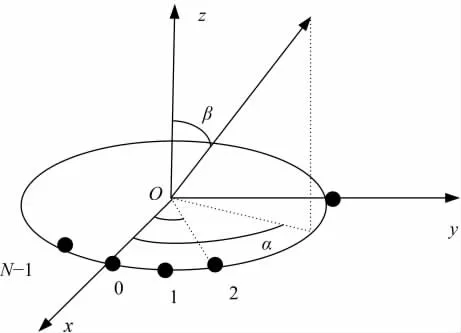
图1 极化均匀圆阵结构图Fig.1 Structure of uniform polarization circular array
第k个信号入射到第m个矢量传感器所获得的两个相互正交的磁场分量表示为:

式中:αk∈[0,2π)为方位角;βk∈[-π/2,π/2]为俯仰角;γk∈[0,π/2];ηk∈[-π,π)分别为极化域中的辅助极化角和相应的极化相位差。
pk=(sinβkcosαk,sinαksinβk,cosβk)为信号的Poynting向量,以原点为参考点,第k个信号在阵元m与参考点之间的相位延迟为:
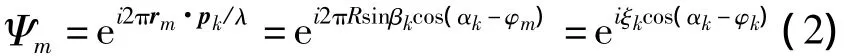
式中:ξk=2πR sinβk/λ,λ为信号波长;第m个电磁矢量传感器的空间位置为rm=(xm,ym,zm)= (R cosφm,R sinφm,0),其 中 φm=2πm/N,m=0,…,N-1。极化均匀圆阵的空域导向矢量为:
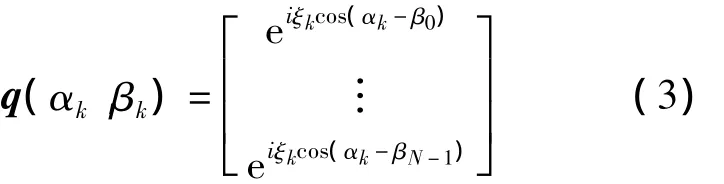
第m个阵元接收到第k个信号的输出为:
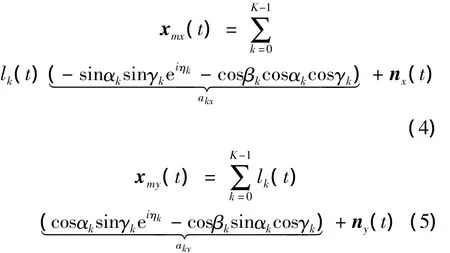
式中:lk(t)为信号的复包络;nx(t)与ny(t)均为噪声矢量。nm(t)=nx(t)+j ny(t)为四元数形式,则第k个信号入射到第m个阵元的接收信号用四元数表示为:
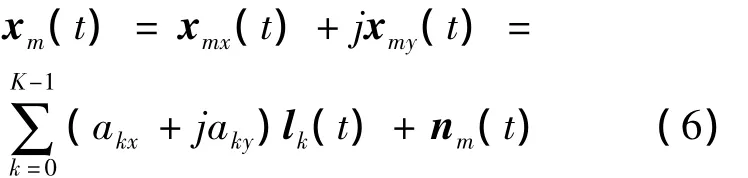
阵列的四元数接收模型表示如下:
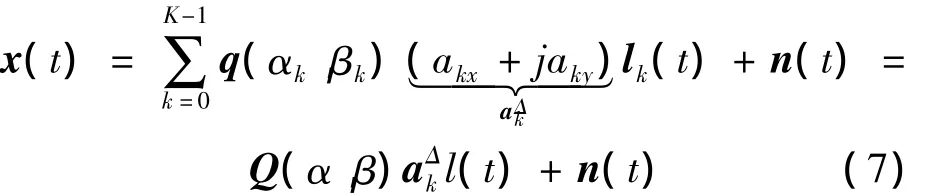
式中:x(t)=[x1(t),x2(t),…,xN(t)]T,x(t)∈HN,Q(α,β)=[q(α0,β0),q(α1,β1),…,q(αK-1,βK-1)]为空域导向矩阵,q(αk,βk)=[q1(αk,βk),…,qN(αk,βk)]T,qm(αk,βk)是第m个阵元的空间相位延迟。l(t)=[l0(t),l1(t),…,lK-1(t)]T是信号矢量,aΔ=diag{,,…,-1}是极化域矩阵,n(t)=[n1(t),n2(t),…,nN(t)]T是四元数形式的均值为零的白噪声矢量。
2 基于Q-MUSIC的UCA阵列信号的多参量估计
2.1 基于四元数的相关矩阵模型的构建
电磁矢量传感器阵列接收信号的协方差矩阵:
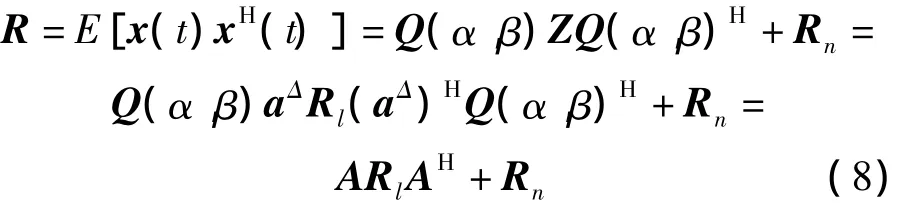
式中:A=Q(α,β)aΔ;Rl=E[l(t)l(t)H],Rn为噪声矢量协方差矩阵,“H”表示共轭转置。A是四元数形式的信号空域-极化角度域导向矢量,由于k个信号是非相关的,令Z表示为
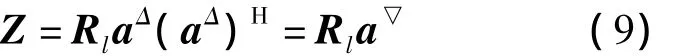
式中:a▽=diag{||2,||2,…,|-1|2},根据式(4)和式(5)得
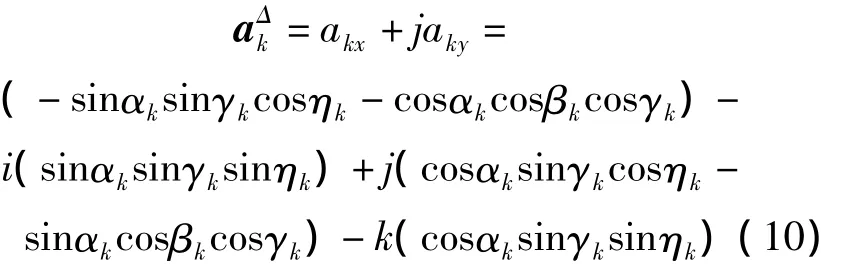

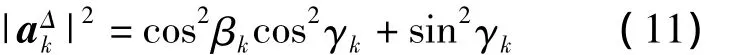
利用信号子空间法推导出关于(αk,βk)的估计,前提是γk≠0,且βk≠±π/2,否则子空间估计算法受限。
基于上述得出的公式,式(8)可表示为

由此可知R是自共轭矩阵,将其用四元数矩阵表示如下

式中:
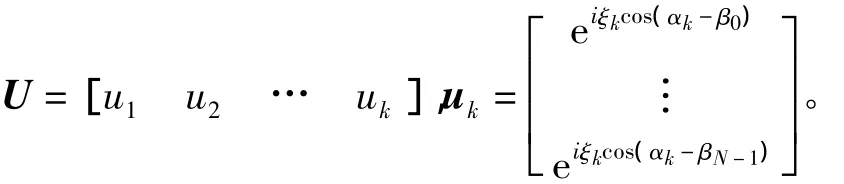
式(11)构成对角阵Λ的对角线上的元素。即
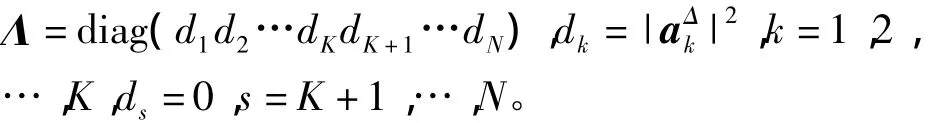
2.2 相关矩阵的特征分析
考虑K个窄带,完全极化的电磁波信号入射到N个电磁矢量传感器组成的均匀圆阵,则阵列接收信号的相关矩阵R的秩为K。
对R进行奇异值分解如下:
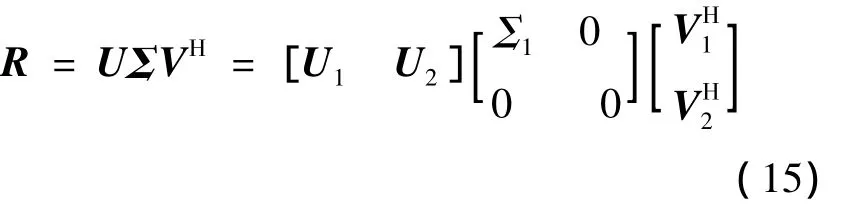
式中:Σ1=diag(σ1σ2… σK),V1对应V前K个矢量,V2对应的是V中后N-K个奇异矢量,同理得到奇异值矢量矩阵U=[U1U2]。矢量空间U1和V1中包含信号的导向信息,称为信号子空间,而空域-极化角度域导向矢量矩阵A与矢量空间U2和V2均正交表示如下:
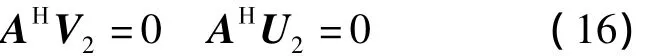
因而称U2和V2为噪声矢量空间。则利用V2中任一奇异值矢量均与A正交的关系,可对信号的DOA和极化信息进行联合估计。
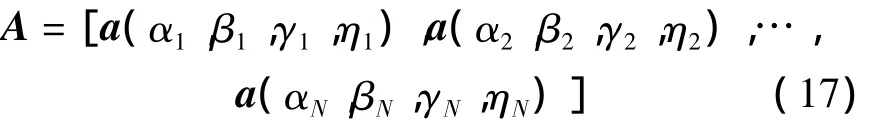
式中:ak(α,β,γ,η)=(α,β,γ,η)·qk(α,β)。
利用噪声子空间原理,谱估计公式可得:
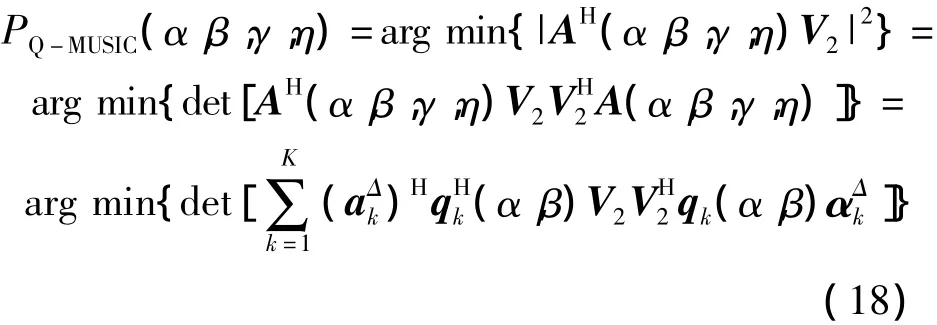
式中:矩阵Z中含有极化信息,而导向矩阵Q(α,β)只包含导向信息,因此可以将式(18)的四维搜索降为二维搜索,在极化参数未知的情况下,提出基于Q-MUSIC算法对(αk,βk)进行估计如下:
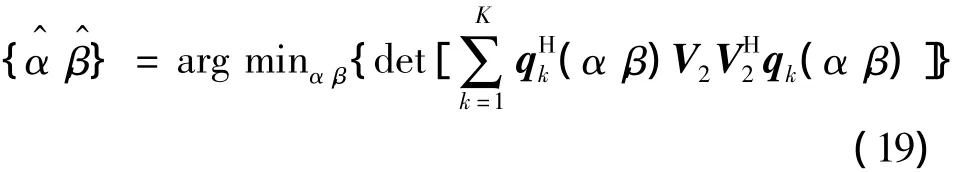
将估计的DOA结果代入式(18)中,则A中只含有信号的极化信息,从而可对(γ,η)进行估计如下:

3 仿真实验及分析
设8个电磁矢量传感器构成均匀圆阵,其半径为R=0.9λ≤λ/(4sin(π/N)),阵列噪声为高斯白噪声,经计算机仿真验证本文算法的有效性。
3.1 实验1
假设两个彼此独立的窄带电磁横向极化平面波信号入射到已给出的极化均匀圆阵模型,信号的DOA参数分别为:α1=60.05°,β1=65.07°,α2=-30.47°,β2=-30.01°;极化参数分别为:γ1=80°,η1=50°,γ2=45°,η2=-90°;信噪比为: snr1=10 dB,snr2=10 dB,采样点数N=1 024。
(1)图2~图4是基于本文提出Q-MUSIC算法的信号相关参数估计仿真图。图2为基于QMUSIC算法的DOA谱估计图。
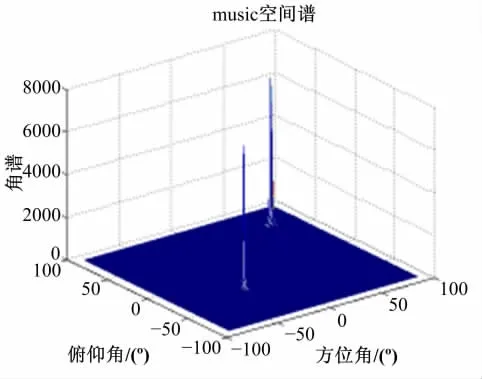
图2 基于Q-MUSIC的DOA谱估计三维图Fig.2 The estimation of DOA based on Q-MUSIC
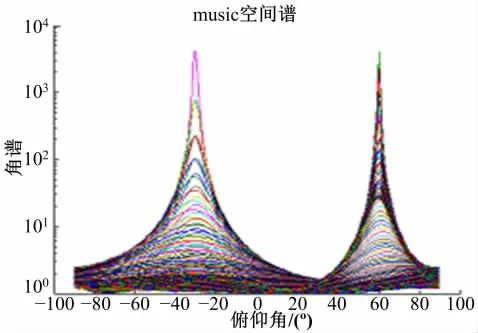
图3 基于Q-MUSIC的俯仰角β估计谱图Fig.3 The estimation of pitch angleβbased on Q-MUSIC
图5~图7是基于传统V-MUSIC的信号多参量估计图。
从图2可以清楚地看到两个谱峰,在极化参数未知的情况下能很好地估计出信号的DOA。
将图3和图4的Q-MUSIC算法分别与图6和图7的V-MUSIC算法相比较,结果表明本文提出算法的谱峰更加尖锐,即增益更高,而且没有“伪峰”的干扰。
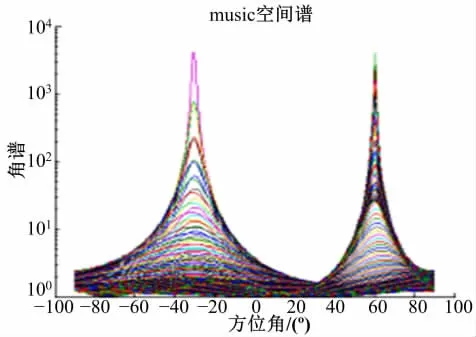
图4 基于Q-MUSIC的方位角α估计谱图Fig.4 The estimation of azimuthαbased on Q-MUSIC
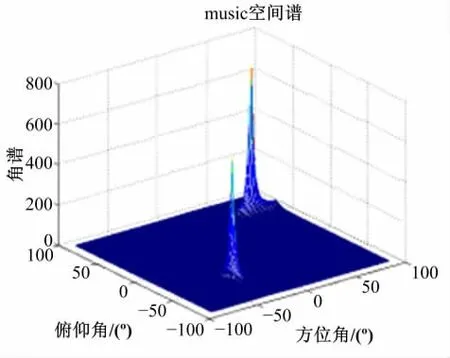
图5 基于V-MUSIC的DOA谱估计三维图Fig.5 The estimation of DOA based on V-MUSIC
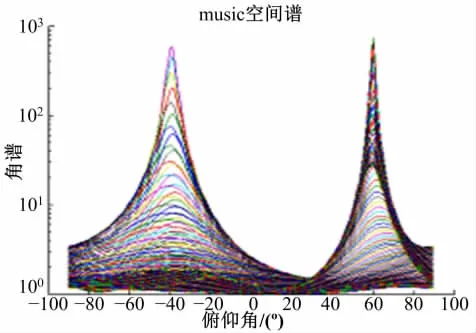
图6 基于V-MUSIC的俯仰角β估计谱图Fig.6 The estimation of pitch angleβbased on V-MUSIC
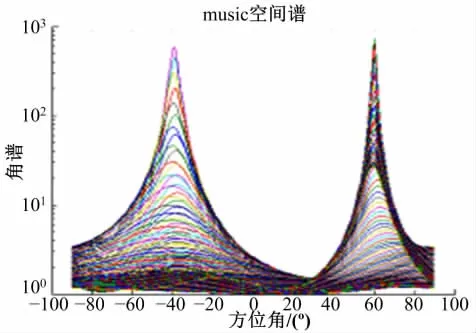
图7 基于V-MUSIC的方位角α估计谱图Fig.7 The estimation of azimuthαbased on V-MUSIC
(2)图8为采样点数N=256时的参数估计仿真图,从图8中可以看出当接收信号序列为短序列时,估计效果依然很好。
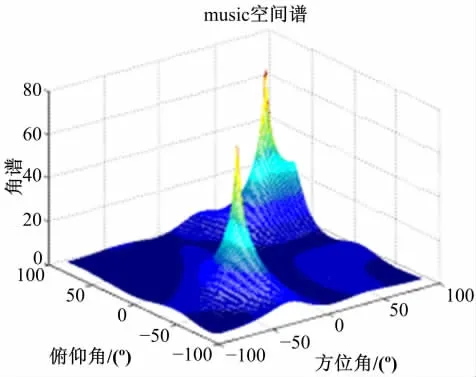
图8 基于Q-MUSIC(N=256)的DOA谱估计三维图Fig.8 The estimation of DOA(N=256)based on QMUSIC
(3)基于Q-MUSIC算法的极化参数估计,以第一个信号为例,如图9所示。

图9 信号1基于Q-MUSIC的极化参数估计谱图Fig.9 The estimation of Signal 1’s polarization parameters based on Q-MUSIC
3.2 实验2
本实验中将参数估计的均方根误差定义为:
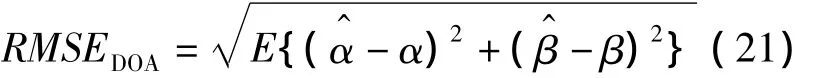
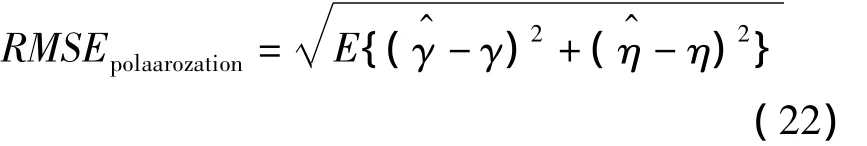
实验条件同实验1的信号1相同,其二维DOA和极化参数的均方根误差随信噪比变化的曲线分别如图10与图11所示,由此可以看出本文算法要优于传统MUSIC算法,尤其在低信噪比情况下参数估计的精度明显提高。
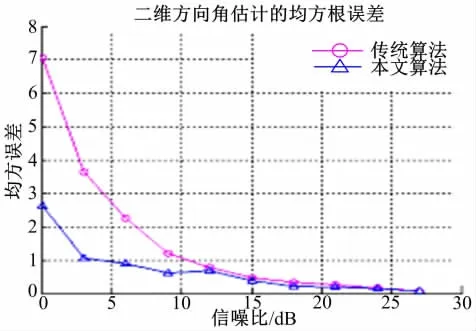
图10 DOA估计的均方根误差曲线Fig.10 The RMS error curve of DOA estimation
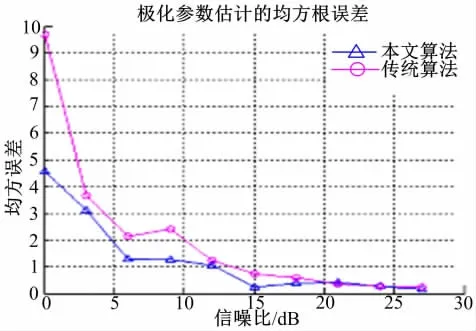
图11 极化参数估计的均方根误差曲线Fig.11 The RMS error curve of Polarization parameters estimation
4 结束语
本文基于均匀圆阵研究了两个相互正交磁偶极子分量,实现了利用四元数理论对电磁矢量传感器阵列信号的DOA与极化参数进行联合估计。结合四元素与极化均匀圆阵的自身特点构造矢量传感器阵列的信号接收模型,提出基于MUSIC的二维参数估计算法。四元素的四维超复数结构使信号模型表达更为简洁,其特有的正交性能更准确地反应电磁信号自身各分量的正交特性。因而基于四元素理论的MUSIC算法比传统MUSIC算法具有更好的资源占用率,仿真实验也证明了该算法有着更好的参数估计精度且分辨率高,抗干扰性强。
[1]王洪洋,王兰美,廖桂生.基于单矢量传感器的信号多参数估计方法[J].电波科学学报.2005,20(1):15-19.
Wang Hong-yang,Wang Lan-mei,Liao Gui-sheng.Parameter estimation ofmultiple source based on uni-vector-sensor[J].Radio Science,2005,20(1):15-19.
[2]徐友根,刘志文.电磁矢量传感器阵列相干信号源波达方向和极化参数的同时估计:空间平滑方法[J].通信学报,2004,25(5):28-38.
Xu You-gen,Liu Zhi-wen.Simultaneous estimation of2-D DOA and polarization ofmultiple coherent sources using an electromagnetic vector sensor array[J].Journal on Communications,2004,25(5):28-38.
[3]Tan K C,Ho K C,Nehorai A.Estimating directions of arrival of completely and incompletely polarized signals with electromagnetic vector sensors[J].IEEE Trans Signal Processing,1999,47(10):2845-2852.
[4]Lei Yin-jie,Chen Cun-jian,Lang Fang-nian.Quaternion singular value decomposition approach to color image de-nosing[C]//IEEE International Joint Conference on Neural Networks(IJCNN2008),2008:131-136.
[5]Pang Hao-chen,Wang Yu-qing,Zhu Ming.Quaternion based assessment method for color image fusion algorithms[C]//CISP2010,2010,5:2341-2346.
[6]武永贵,王树勋,汪飞.四元数和超复数在加性高斯噪声背景下二维谐波频率估计中的应用[J].吉林大学学报:工学版,2006,36:122-125.
Wu Yong-gui,Wang Shu-xun,Wang Fei.Two-dimensional harmonics frequency estimation in additive gaussian noise background based on quaternion and hypercomplex[J].Journal of Jilin University(Engineering and Technology Edition),2006,36:122-125.
[7]汪飞,王树勋,陈巧霞.基于Hamilton四元数矩阵奇异值分解的二维谐波频率参量估计[J].电子学报. 2007,35(12):2441-2445.
Wang Fei,Wang Shu-xun,Chen Qiao-xia.Parameters estimation of two-dimensional harmonics based on singular value decomposition ofquaternionmatrix[J].Acta Electronica Sinica,2007,35(12):2441-2445.
[8]Miron S,LeBihan N,Mars J I.Quaternion-MUSIC for vector-sensor array processing[J].IEEE Transactions on Signal Processing,2006,54(4):1218-1229.
[9]Seberry J,Finlayson K,Adams SS.The theory of quaternion orthogonal designs[J].IEEE Transactions on Signal Processing,2008,56(1):256-265.
[10]汪飞,王树勋,张坤雷.色噪声背景下基于四元数MUSIC方法的矢量阵列信号参量估计[J].通信学报,2008,29(5):133-140.
Wang Fei,Wang Shu-xun,Zhang Kun-lei.Parameters estimation of vector-sensor array in colored noise based on quaternion-MUSIC[J].Journal on Communications,2008,29(5):133-140.
[11]Gong Xiao-feng,Xu You-gen,Liu Zhi-wen.Quaternion ESPRIT for direction finding with a polarization sentive array[C]//ICSP2008,2008:378-381.

