基于小波包-隐马尔科夫模型的机床加工状态识别
谢锋云
(华东交通大学机电工程学院,江西南昌330013)
机床加工状态的识别,尤其是机床加工中的颤振状态的识别是非常重要的。加工过程中如果发生颤振,会严重降低加工质量、切削效率,并会降低刀具、机床的使用寿命等[1]。识别过程主要由特征提取和模式识别组成。过去的研究中,在特征提取方面提出了两类方法:一种是时域特征提取,主要采用传统的概率统计分析的方法,缺点是机床加工状态变化过程中,时域信号是一个渐变的过程;另一种是频域特征提取,在不同的加工状态中,系统在频域内的能量分布有着显著的差别。如在时域中颤振振幅刚刚开始增大阶段,加工振动能量就已集中在一个十分窄的频段内,则在频域内提取的特征量比在时域内提取的特征量具有更大的准确性。
作者提出基于小波包-HMM(隐马尔科夫模型)的机床加工状态识别方法,利用小波包分解进行特征提取,分别求出各种状态在不同频带上的能量百分比,作为HMM的输入观测特征向量;按照HMM模式识别方法,训练标准样本模型,依据测试样本的最大对数似然值,对机床的加工状态进行状态识别。
1 小波包分解与HMM基本原理
小波变换是非平稳信号处理比较理想的数学工具,小波函数定义:设Ψ(t)为一平方可积函数,如果其傅里叶变换Ψ(ω)满足
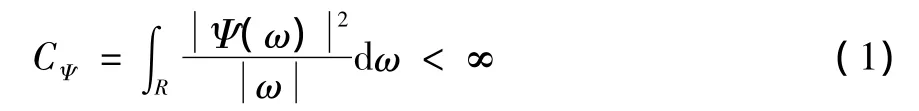
则称Ψ(t)为一个基本小波或母小波。
小波分析是一种时间窗和频率窗均可改变的时频局部化分析方法。把信号分解成位于不同频带和时段内的各个成分,即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,所以被誉为数学显微镜。
小波包分解是一种频带分析技术,是从小波分析延伸出来的一种对信号进行更加细致地分析与重构的方法。小波包分解不仅分解了信号低频部分,同时也对高频段进行了分解,通过对信号在不同尺度上进行分解和重构,能得到原信号在不同频段上分布的详细信息。图1所示为3层小波包分解的树形结构。对小波包分解系数重构,可以提取从低频到高频8个子频带的小波包能量。当加工状态发生改变时,各频带内信号特征会有较大变化。进行识别时,可以通过频带能量谱构造一个特征向量,作为模式识别的输入[2-4]。
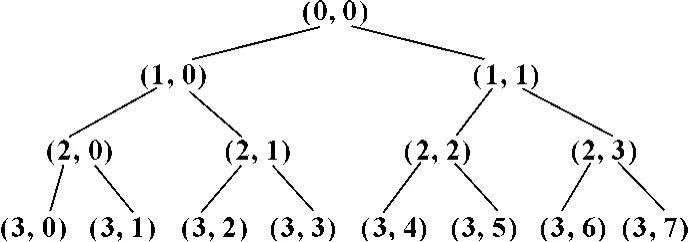
图1 小波包变换的树形结构
HMM是一个双重的随机过程,状态不能直接观测,但能通过观测向量序列观察,已成为信号统计处理强有力的工具,并在语音识别、生物信息科学、故障诊断领域获得广泛的应用。HMM通常记为λ= (N,M,π,A,B),其中:N表示模型的隐状态数目;M为可能的观测数目;π表示初始状态概率矩阵,πi=P(q1=i)表示时刻1选择某个状态的概率;A为状态转移概率矩阵,A中的每个元素aij表示从状态 i转移到状态 j的概率,aij=P{qt+1=Sj| qt=Si},1≤i,j≤N;B表示观察值概率矩阵,B中的每个元素bj(k)表示t时刻状态j出现观测值vk的概率,bj(k)=P{vk|qt=Sj},1≤i,j≤N。矩阵A的维数为N×N,B的维数为N×M,HMM也可简记为λ=(π,A,B),一个HMM也正是通过π、A、B的不同分布来描述不同的随机过程[5-7]。
2 信号处理
2.1 数据采集
图2是在装有交流永磁同步电动机的CNC立式机床 (油欣精机VL-850HR+P)上进行车削加工的加速度信号图,由压电式加速度传感器 (PCB 356A15)获取加工时刀尖加速度信号,采用高速数据采集系统LMS Test.Lab中的Signature Testing功能模块进行信号采集,并以10 240 Hz的采样频率实现加速度信号采集,最后输入计算机保存和显示。图3为数据采集示意框图。

图2 机床加工加速度信号

图3 数据采集框图
2.2 频谱分析
通过传统的时域分析方法很难得出机床加工的状态分布。这里对图2采用FFT频谱分析方法,频谱分析如图4所示。在图4中,依据不同区域相同频率段的幅值有明显的不同,把机床加工状态分为Ⅰ、Ⅱ、Ⅲ3个区域,分别为稳定状态、过渡状态、颤振状态。从图4(c)可知,发生颤振的频率约为2 000 Hz,这为防止颤振的发生提供了一种有效解决的思路。
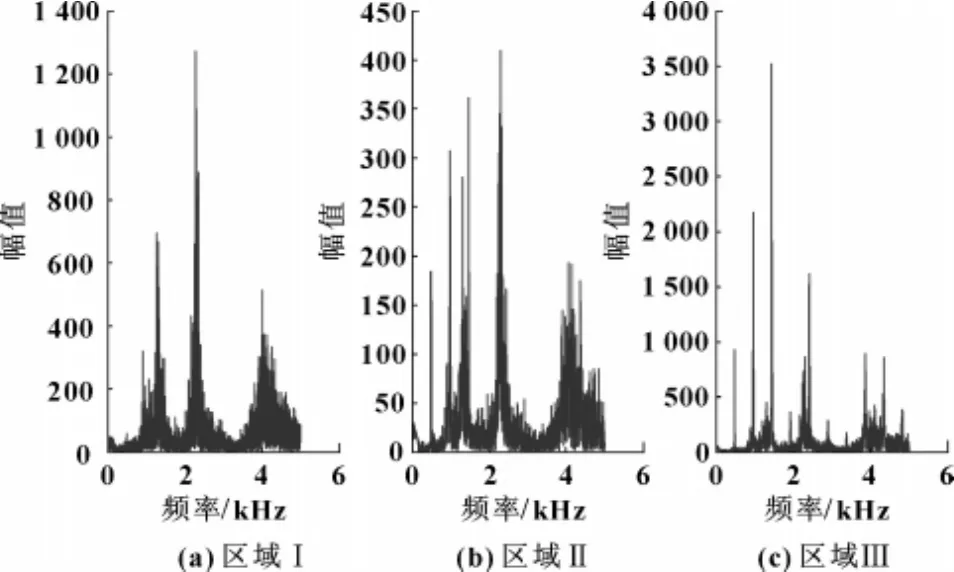
图4 加速度信号FFT频谱分析
2.3 小波包分解
采用小波包分解特征提取的方法,把不同区域的加速度信号经过小波基sym1进行3个分析层的小波包分解,加速信号的能量被分解到23=8个正交频带上。信号的采样频率为10 240 Hz,分解到的8个频率区间如表1所示。

表1 三层小波包分解各节点所对应的频率区间 Hz
信号在各频带上的能量总和与原信号的能量一致,每个频带内的加工信号表征原信号在该频率范围内的加工信息。当机床加工状态发生变化时,各个频带的能量分布将会有很大的变化,即机床加工信号经小波包分解后,在各频带上的投影与正常状态下的不同。因此可将加工信号在各频带投影序列的能量或与能量对应的值作为特征向量,这是一种基于频带-能量-加工状态的特征提取方法。图5为从加速度信号区域Ⅰ、Ⅱ、Ⅲ中采样后,分别进行小波包分解后各节点对应的能量百分比 (在相同节点中,左为稳定区域,中为过渡区域,右为颤振区域)。

图5 小波包分解
3 状态识别
识别的步骤如下:(1)求取观测输入特征向量; (2)求取初始模型;(3)训练标准样本;(4)识别测试样本。
从图5中可以容易得到,不同状态区域采集到的加速度信号经过小波包分解,得到的能量百分比有着明显的区别。把小波包分解的能量百分比作为HMM的观测输入值,利用Lloyd算法[8]进行编码,从而得到不同状态观测输入特征向量。不防定义初始模型λ中数值参量N=3,M=3,根据实验得知机床加工的初始状态为稳定状态,初始模型λ中π设为π=(1,0,0),A、B可以由计算机随机生成,通过HMM的B-E算法进行优化。从3个区域中选取样本,分别作为标准样本输入,代入初始模型中进行训练,得出各个状态的优化模型,组成优化模型库。从加工信号中随机选取测试样本,经过相同的信号处理,测试样本代入优化模型库,求出相应的对数似然值,最大的对数似然值相应的状态即为识别的结果。表2为一组HMM状态识别例子。
表2中,通过对每一行数值进行比较,黑体部分的对数似然值-5.753 5,-16.821 3,-5.365 3为最大值。由HMM模式识别方法可知,黑体对应的值为识别的结果,即稳定测试样本识别结果为稳定,过渡测试样本识别结果为过渡,颤振测试样本识别结果为颤振,识别结果与测试样本结果一致,状态识别结果正确。
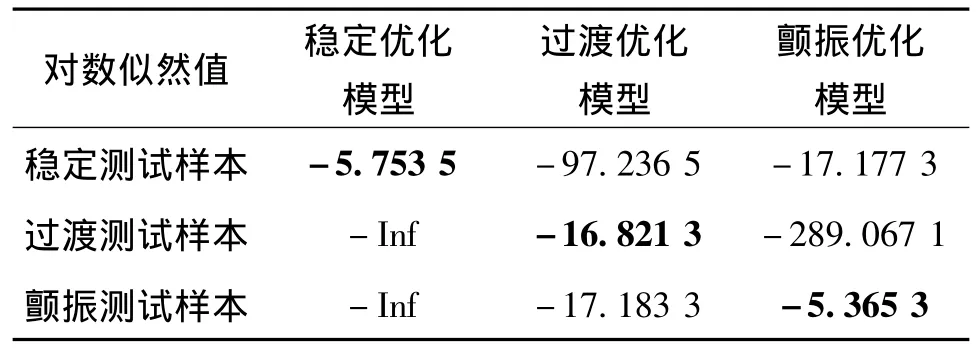
表2 HMM状态识别
4 结束语
利用小波包分解特征提取的方法,分别求出各种状态在不同频带上节点的能量百分比,并把它作为HMM的输入特征值,利用Lloyd算法对特征值进行编码得到观测特征向量,建立3种标准状态的训练优化模型库,通过HMM模式识别方法,把测试样本代入优化模型库中,对机床的加工状态进行了识别。结果表明,该方法状态识别结果正确。这种频带—能量—加工状态识别方法解决了时域中渐变问题,是一种工程中状态识别的有效方法。由于观测信号可能存在误差,小波包分解边界能量重叠问题将对结果产生一定的影响,在今后的研究中,可以考虑在观测值、HMM识别中引入区间概率,通过区间概率提高结果的可靠性。
【1】汤爱君,马海龙.机床再生颤振系统研究现状的综述[J].机床与液压,2007,35(8):223-225.
【2】周飞鹏,郑昌祥,王宁.基于小波包分析的提升机液压泵故障研究[J].煤矿机械,2011,32(2):246-247.
【3】高英杰,孔祥东.基于小波包分析的液压泵状态监测方法[J].机械工程学报,2009,45(8):80-88.
【4】谢秀娴,付攀,曹伟青.声发射和小波包分解技术在刀具磨损状态中的应用[J].中国测试技术,2006,32(2):40-42.
【5】陶新民,徐晶,杜宝祥,等.基于小波域隐马尔可夫模型故障诊断方法[J].振动与冲击,2009,28(4):33-38.
【6】朱明,郭春生.隐马尔可夫模型及其最新应用与发展[J].计算机系统应用,2010,19(7):255-259.
【7】RABINER L R.A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition[C]//Proceedings of the IEEE,1989:257-286.
【8】SABIN M J,GRAY R M.Global Convergence and Empirical Consistency of the Generalized Lloyd Algorithm[J].IEEE Transactions on Information Theory,1986,32(2): 148-155.

