调制相位差对TDLAS信噪比的影响

董跃辉，吴尚谦，翟 维，皇甫张棣，刘爱英

（昆明理工大学理学院，昆明650500）

调制相位差对TDLAS信噪比的影响

董跃辉，吴尚谦*，翟 维，皇甫张棣，刘爱英

（昆明理工大学理学院，昆明650500）

用可调谐二极管激光吸收光谱技术检测气体时，不同的调制相位差结果不同。为了提高谐波检测灵敏度，采用同时考虑频率调制与振幅调制的方法分析和提取二次谐波信号，推导了相位差与二次谐波信号光电流和残余幅度调制噪声光电流的函数关系表达式，通过模拟实验分别取得了二次谐波信号和残余幅度调制噪声随相位差的变化趋势，并重点分析了相位差对信噪比的影响。结果表明，振幅调整和频率调制之间的相位差对信噪比的影响很大，与典型值π/2时相比，最大降幅为59.18％；调制相位差是继残余幅度调制之外，影响信噪比的一个重要因素。

光谱学；相位差；频率调制；可调谐二极管激光吸收光谱；信噪比

引 言

随着激光技术的迅速发展，可调谐半导体激光成为痕量气体谐波检测的理想光源［1］。可调谐二极管激光吸收光谱（tunable diode laser absorption spectroscopy，TDLAS）技术是利用半导体激光器的波长扫描和电流调谐特性来实现痕量气体吸收谱线谐波检测的一种气体检测技术。从20世纪80年代至今，国内外许多科研工作者已经将TDLAS技术应用到各个研究领域，并在提高系统的检测灵敏度方面取得了显著成果［1］。

调制相位差即同时考虑振幅调制和频率调制时二者之间的相位差。为了提高检测灵敏度，可以通过改善信噪比的方法，即增大信号以及抑制噪声。REID等人［2］采用傅里叶展开的方法来提取二次谐波，并选取二次谐波峰值作为检测信号，得到相对调制幅度m=2.2时二次谐波信号取得最大值。而在实际检测中，谷值对检测也有影响，TU等人［3］将峰谷差值作为检测信号，得出m=3.1时二次谐波信号取得最大值。BJORKLUND［4］首次提出了残余幅度调制也是噪声的观点；TU等人详细介绍了TDLAS噪声来源并对二次谐波进行了噪声分析。当调制频率较高时，低频噪声即1/f噪声被抑制，从而达到降噪的目的。DHARAMSI［5］采用直接去掉虚部的方法研究了相位差对谐波信号的影响，同时验证了振幅调制与频率调制相结合（amplitude modulation and frequencymodulation，AM-FM）的方法适用于纯频率调制（frequency modulation，FM）方法。WU和CAI等人［6-7］基于AM-FM方法分别做了相位差为π/2条件下的二次谐波线型和信噪比（signal-to-noise ratio，SNR）的研究。

为了研究AM-FM相位差对SNR的影响，本文中结合WERLE［8］的算法，同时考虑AM和FM以及二者之间的相位差3个因素，分别推导出相位差对二次谐波信号以及对残余振幅调制（residual amplitudemodulation，RAM）噪声影响的表达式，并对其进行模拟实验，最后分析AM-FM相位差对信噪比的影响。用理论推导和模拟分析结合来阐述可调谐二极管激光吸收光谱检测系统的信噪比与频率调制和振幅调制之间的相位差的密切关系。

1 原理技术

在TDLAS检测技术中，根据半导体激光器本身的特性，激光频率发生变化的同时，伴随着振幅（功率）也在发生变化，从而产生RAM，称此方法为FMAM调制。系统构成上与之前的研究相同［6-7］，利用温度控制器控制激光器温度唯一恒温，将调制信号通过电流控制器直接加载到激光器注入电流上，出射的经过调制的激光通过吸收池后由光电探测器探测，通过光电转换后的电信号送入锁相放大器进行二次谐波信号的提取，最后输入计算机完成信号的数据处理。经过调制的激光，其输出光电场表达式为：

式中，E0为未调制时的光电场，M为幅度调制指数（激光的RAM），φ为AM-FM之间的相位差，β为频率调制指数，ωm为调制角频率，ωl为激光的载波角频率，t为时间。这里的β是为了与参考文献中出现的调制指数m相对应，它们的关系是m=β×ωm/Δω，以下都用m来表示。引入贝塞尔函数后修改（1）式见参考文献［7］中的推导。

1.1 二次谐波信号的推导

经过调制后的激光通过充满待测气体的吸收池后，由光电探测器探测得到的经过吸收衰减后的光电场为：

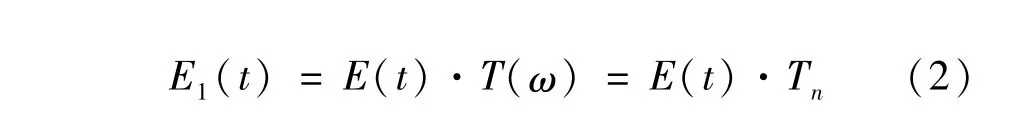
式中，T（ω）=exp［-δ（ω）-iφ（ω）］为复传输函数（复透光率），实部 δ（ω）为吸收衰减系数，虚部φ（ω）为色散系数。由于受调制的激光可以用谐波分量表示，所以传输函数也可以按谐波分量表示为：Tn=exp（-δn-iφn）。则从吸收池出射的光电流表示为i（t）=E1（t）·E1（t）*，把（2）式代入，将从激光器出射的激光也通过电场平方律关系表示成i0，整理后可得：

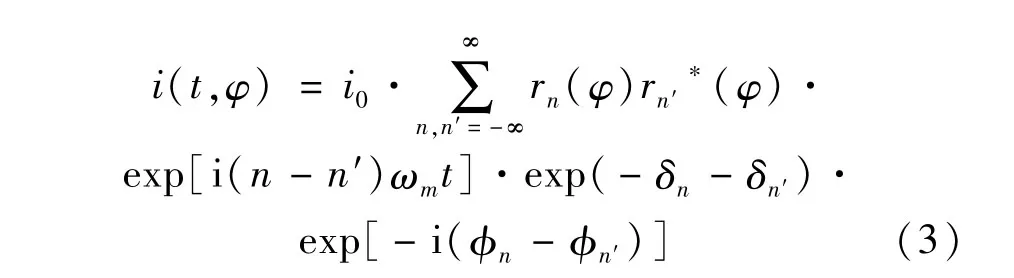
为了提取二次谐波，取n=n+1，n′=n-1。则有：

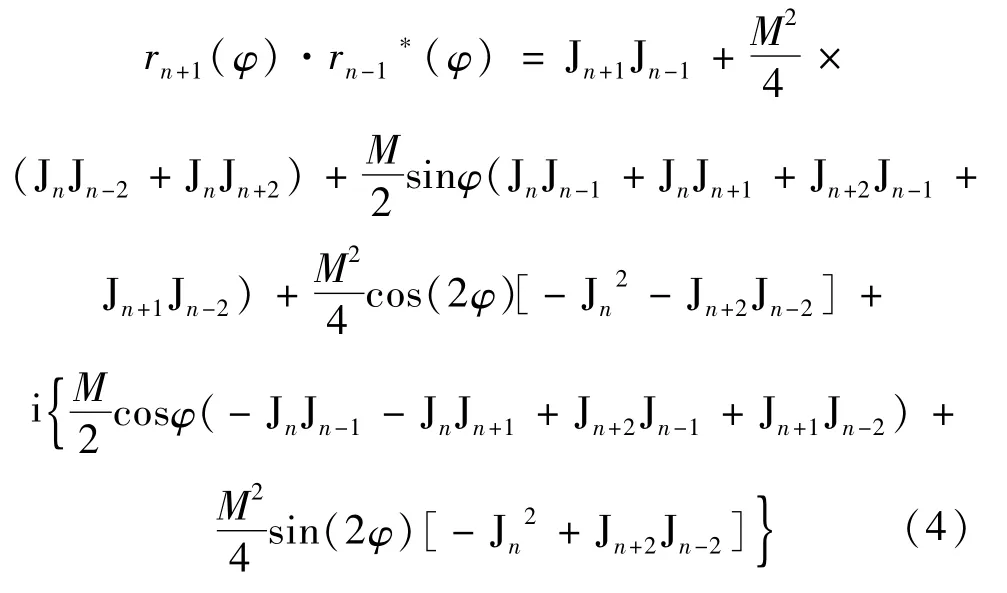
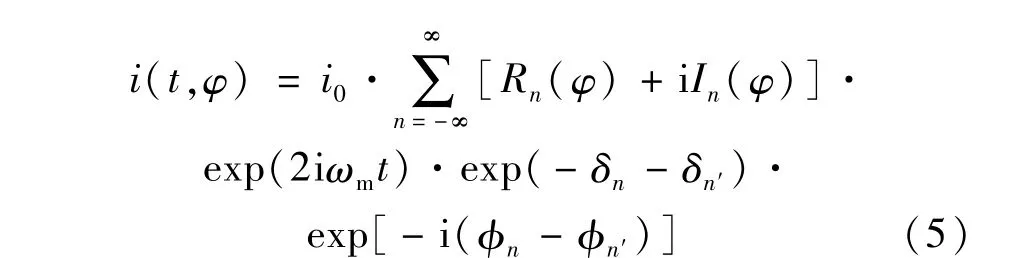
式中，光电流既包含了FM-AM的相位差，又将虚部和实部分离开来表示，使谐波表达式包含的信息更丰富。光学厚度δn里面含有吸收线型函数，考虑自然展宽时，用洛伦兹分布函数代入计算，实部Rn和实际检测中的吸收衰减信号相对应，所以模拟计算时只考虑实部并忽略色散的影响，即令exp［-i（φnφn′）］=1，二次谐波分量则可以表示为：

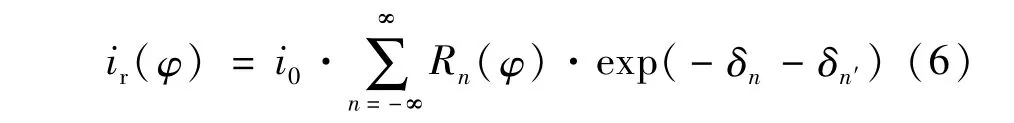
由上式可知，二次谐波信号是AM-FM的相位差的函数，由于谐波信号和RAM噪声信号是信噪比的两个重要参量，有必要分析相位差的变化对残余幅度调制噪声的影响，从而达到对信噪比影响的研究。

1.2 二次谐波RAM噪声

对激光进行频率调制的同时，会伴随着产生振幅调制，而RAM噪声是影响信噪比的一个重要因素。RAM噪声信号即为没有吸收时的二次谐波背景信号，其值即为基线值。对于二次谐波，由（3）式和（6）式可得RAM噪声随相位差变化的表达式为：

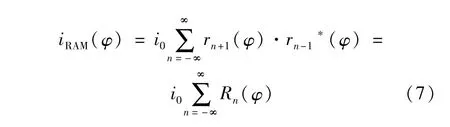
2 相位差对二次谐波信号以及RAM噪声的影响

为了验证相位差对信号的影响程度，采用（6）式进行模拟计算。相位差从0到2π之间变化，每间隔π/12取值，共取25个不同的相位差计算点。计算时其它参量的取值为：β=1000，M=0.05，光学厚度δ=α·L/｛π［1+（（ωl+nωm-ω0）/Δω）2］｝，其中吸收中心的吸收系数α=0.01，吸收光程L= 1m，吸收中心频率ω0=0，洛伦兹半峰全宽Δω=1，n为贝塞尔函数的n取值，这里取为β的1.5倍，ωl变化从-10～10。

在信号的处理上，如图1中内插图所示，取二次谐波的峰值与左边谷值的差值作为检测信号。通常当m=2.2时峰值达到最大［2］；当m=3.1时峰谷差值达到最大［3］。为了便于比较，本文中计算m=2.2和m=3.1时峰谷差值随着相位差的变化趋势。二次谐波信号随FM-AM相位差的变化计算结果如图1所示，图1中的两条线分别代表m=2.2和m= 3.1时的二次谐波信号随相位差的变化。

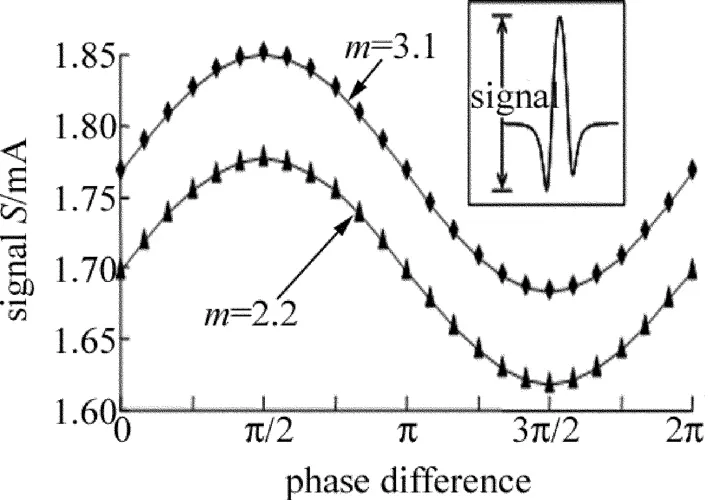
Fig.1 Relationship between signal and phase difference when m=2.2 and m=3.1

计算结果表明，信号的峰谷值都发生了变化，相位差造成左右谷值不等，左右谷值的变化都是以2π为周期，且变化趋势相同，只是延迟了相位π。因此模拟计算时左右谷值选取其一即可。

从图1可以看出，m=2.2时，不同相位差对应的信号值S最大为1.776mA，最小为1.618mA，相位差为0时是1.698mA；图1显示当m=3.1时，S最大为1.850mA，最小是1.683mA，相位差为0时是1.767mA。两图都是在相位差为π/2时取得最大值，相位差为3π/2时取得最小值，其值随着相位差的变化趋势也相同，类似于一个正弦函数，m=2.2时的信号变化明显比m=3.1时小，最小信号与π/2时相比，信号最大变化分别为8.90％和9.03％。

按照同样的计算条件，根据（7）式经过模拟实验，计算得到的RAM噪声会随着相位差的变化而有所改变，将相位差的取值更精细，如图2所示。

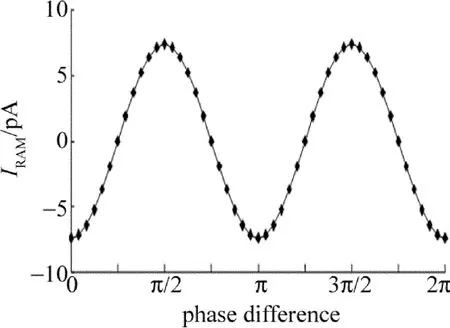
Fig.2 Relationship between RAM noise and phase difference

从图2可以看出，RAM噪声光电流随着相位差发生周期性变化，变化周期为π，振幅即为当相位差为π/2时的7.4pA。在一个周期内，相位差为0时，取得最小值-7.4pA，该值与π/2时的值关于零点对称，RAM噪声随相位差的最大变化倍率为200％。调制相位差对RAM噪声光电流大小有影响，由此可知，该相位差也会影响信噪比计算时的RAM噪声均方电流。

3 相位差对SNR的影响

TDLAS的噪声来源主要包括探测器散粒噪声、探测器热噪声、电流直接调制时引起的偏移噪声（RAM噪声）、激光光源引起的过载噪声（即1/f噪声）和因激光的相干性产生的标准具干涉条纹噪声［9］。由于标准具干涉条纹噪声具有系统依赖性，在计算中不予以考虑。因此TDLAS检测系统的信噪比可以表示成［10-11］：

式中，分子是信号均方电流，分母上各项依次是散粒噪声、热噪声、RAM噪声、噪声的均方电流。考虑二次谐波检测，可以把上式展开成如下形式：

式中，S（φ）是前面提到的随相位差变化的信号值；η是探测器的量子效率；h是普朗克常量；ν0是光频率；P0是入射到探测器上的激光总功率；Δf是等效测量带宽；kB是玻尔兹曼常数；T是绝对温度；Rl是探测电子输入阻抗；σp是激光功率波动变化率；f是调制频率；b是频率指数，典型值为1。表1中给出了SNR参量取值及单位。

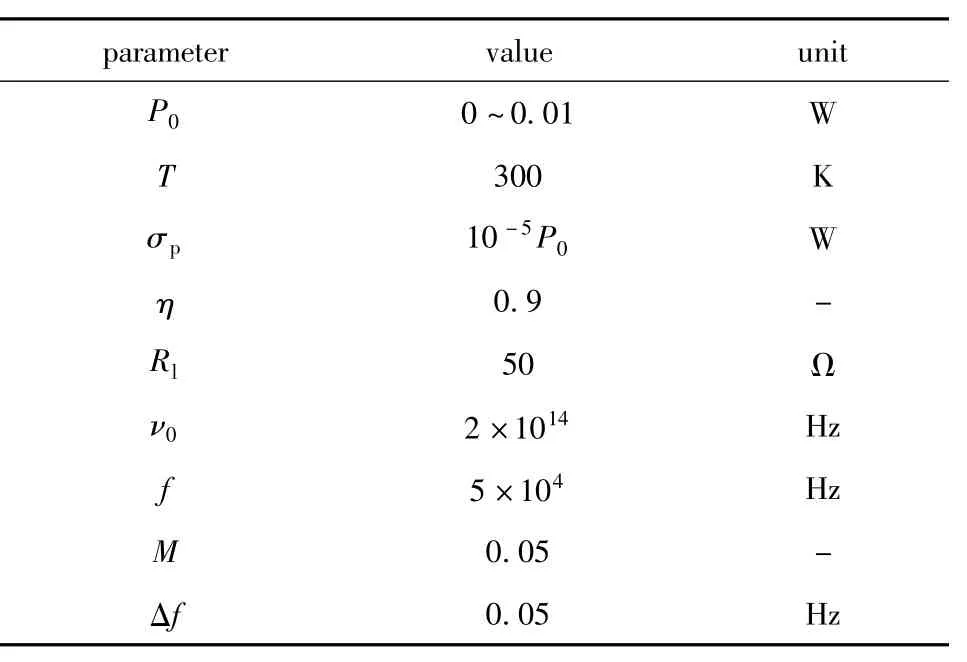
Table 1 Typical value of SNR parameters

参考表1中的参量典型取值，此时RAM噪声是主要噪声，在m为2.2和3.1两种情况下，相位差间隔π/12时，分别计算对应的信号值S，IRAM噪声值和扫描激光功率可获得信噪比随相位差的变化曲线，由于S和IRAM的取值的周期变化性，则所得信噪比曲线是重合后的13条，而非25个相位差值对应的25条。如当相位差为0，π，2π时，SNR是相同的；而π/2和π/2时分别为1条。由于曲线太密集，选取其中的8条曲线作图，如图3和图4所示。

Fig.3 Effect of phase difference on SNR when m=2.2

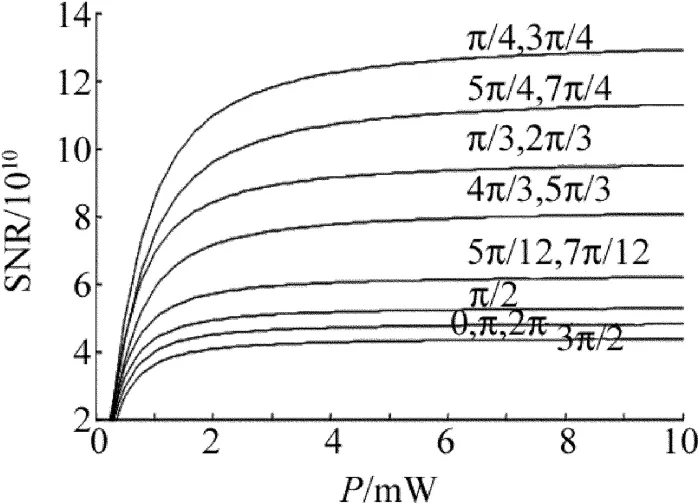
Fig.4 Effect of phase difference on SNR when m=3.1

从以上两图可看出，随着激光功率的增大，SNR迅速增大并逐渐趋于平滑，而且SNR随着相位差的变化十分明显，图中信噪比较大的5条曲线之间间隔很大，即SNR相差很大。图3中，φ为π/4和3π/4时，SNR能取得最大值11.916×1010，将其它值与之相比较，例如相位差φ=0时的信噪比4.445×1010，相对下降了62.70％；φ=3π/2时，SNR取得最小值4.034×1010，下降了66.15％；φ=π/2时对应的SNR为4.864×1010，与最大SNR相比下降了59.18％。图4中，φ=0时的信噪比4.812×1010、φ=3π/2时的最小信噪比4.364×1010以及φ=π/2时的信噪比5.273×1010，与最大信噪比12.912× 1010相比，其SNR分别下降了62.73％，66.20％和59.16％。从图3和图4以及定量分析很容易发现，两种条件下，SNR随着相位差的变化趋势相同但取值差异很大；相位差对SNR的影响程度很大，当取值不为典型值π/2时，可能导致信噪比大幅度上升或者小幅度下降。

4 结 论

对于二次谐波检测，为了研究相位差对信噪比的影响，采用同时考虑振幅和频率调制两种调制的方法。假定M，β两种调制系数都为固定值，分别推导了AM-FM相位差与信号、RAM噪声的关系式。从0到2π之间间隔π/12取值进行模拟计算，考虑信号越大越有利于检测，取峰值与左边谷值的差值作为检测信号，对结果进行分析得到二次谐波信号随着相位差的变化呈周期性的变化，其形状类似一个正弦曲线，当m=2.2和m=3.1都是在相位差为3π/2时取得最小信号值，与相位差π/2时的最大信号值相比，相对变化了8.90％和9.03％。信号变化的同时，RAM噪声也随着相位差做周期为π的变化，最多可达200％。当m=2.2和m=3.1，与最大SNR相比，信噪比最多分别下降66.15％和66.20％，与典型值π/2相比，最大变化幅度为59.18％和59.16％。结果表明，除了之前研究的残余幅度调制影响SNR，相位差也是影响SNR的一个重要因素，本文中的结果可以为实际检测中提高检测灵敏度提供理论指导。

［1］SHU XW，ZHANG Y J，GENG H，et al.Study on phase shift auto-balanced laser absorption spectroscopy［J］.Laser Technology，2011，35（5）：618-621（in Chinese）.

［2］REID J，LABRIE D.Second-harmonic detection with tunable diode lasers：comparison of experiment and theory［J］.Applied Physics，1981，B26（3）：203-210.

［3］TU X H，LIUW Q，WANG T D，et al.Noise analysis of secondharmonic detection with tunable diode laser absorption spectroscopy［J］.Chinese Journalof Quantum Electronics，2006，23（4）：22-26（in Chinese）.

［4］BJORKLUND G C.Frequency-modulation spectroscopy：a new method formeasuringweak absorptionsand dispersions［J］.Optics Letters，1980，5（1）：15-17.

［5］DHARAMSIA N.A theory ofmodulation spectroscopy with applications of higher harmonic detection［J］.Journal of Physics，1996，D29（3）：540-549.

［6］WU A，WU Sh Q，CAIY，etal.Effectof RAM on WMSsignal line shape［J］.Laser Technology，2012，36（3）：357-360（in Chinese）.

［7］CAIY，WU Sh Q，WU A，etal.Study on calculationmethod of detection limitbased on wavelengthmodulation spectroscopy［J］.Laser Technology，2012，36（3）：390-393（in Chinese）.

［8］WERLE P.A review of recent advances in semiconductor laser based gas monitors［J］.Spectrochimica Acta，1998，A54：197-236.

［9］WU Sh Q，KIMISHIMA T，YOSHIIY，et al.Reduction of fringe noise in wavelength modulation spectroscopy using a one-dimensional focal plane array［J］.Optical Review，2002，9（5）：189-192.

［10］BOMSE D S，STANTON A C，SILVER JA.Frequencymodulation and wavelengthmodulation spectroscopies：comparison of experimentalmethods using a leadsalt diode laser［J］.Applied Optics，1992，20（6）：718-731.

［11］SILVER JA.Frequency-modulation spectroscopy for trace species detection：theory and comparison among experimentalmethods［J］.Applied Optics，1992，31（6）：707-717.

Effect ofmodulated phase difference on TDLAS signal-to-noise ratio

DONG Yue-hui，WU Shang-qian，ZHAIWei，HUANGFU Zhang-di，LIU Ai-ying
（Faculty of Science，Kunming University of Science and Technology，Kunming 650500，China）

When using tunable diode laser absorption spectroscopy（TDLAS）for gas detection，modulation phase difference would make the result different.In order to improve harmonic wave detection sensitivity，frequency modulation and amplitude modulation were simultaneously chosen to analyze and extract the second harmonic wave signal.The functional relationship expression between the phase difference and the photo-electron current of the second harmonic wave and the residual amplitudemodulation noise was also derived.From the simulation experiments，the variation trend of the second harmonic wave signal and the residual amplitude modulation noise with the phase difference were obtained.And then，the effect of phase difference on signal-to-noise ratio（SNR）was analyzed.The results show that the phase difference between amplitudemodulation and frequency modulation has a significant impact on SNR.The largest drop is 59.18％ when compared with the typical value of phase difference ofπ/2.Modulation phase difference is another importantaffecting factor of SNR besides residual amplitudemodulation.

spectroscopy；phase difference；frequency modulation；tunable diode laser absorption spectroscopy；signal-to-noise ratio

O433.5+1

A

10.7510/jgjs.issn.1001-3806.2013.04.018

1001-3806（2013）04-0498-05

董跃辉（1987-），女，硕士研究生，主要从事激光气体检测和光学雨量计的研究。

*通讯联系人。E-mail：wusq＠kmust.edu.cn

2012-09-10；

2012-10-18