内嵌围护墙板对钢框架抗侧力性能的影响效应

金晓飞，孟永杰，杨晓杰，范 峰，曹正罡，李景芳

(1.哈尔滨工业大学 土木工程学院，150090 哈尔滨;2.中国建筑股份有限公司技术中心，101300 北京;3.中国中元国际工程公司，100089 北京)

装配式钢结构建筑体系因其“节能、低耗、省时”三大特点势必成为房屋建筑业未来发展的方向之一.已有研究和实践经验表明，墙体围护结构的问题是制约钢结构住宅长足发展的主要原因之一［1］.《建筑抗震设计规范》(GB50011—2010)规定围护墙和隔墙应考虑对结构抗震的不利影响，避免不合理设置而导致主体结构的破坏.《轻型钢结构住宅技术规程》(JGJ 209—2010)指出，忽略填充墙的侧向刚度作用，对抗震不利，宜利用镶嵌填充的轻质墙体侧向刚度对整体结构抗侧移的作用，墙体的侧向刚度应根据墙体材料和连接方式的不同由试验确定.目前对于砌体填充墙与框架协同作用的相关研究较多，但是对于镶嵌墙板，通常认为其对结构影响较小，因而相关研究较欠缺.李国强等［2］曾对带ALC(蒸压轻质加气混凝土)墙板钢框架结构进行了水平静力及低周反复加载试验，试验得出内嵌墙板会使框架刚度增大50% ～70%，承载力提高65%左右.该试验只是针对确定形式的墙板及跨度进行试验并且没有考虑竖向荷载及墙体开洞的影响.许刚［3］曾针对ASA板(轻质节能环保型复合材料)镶嵌式墙板钢框架在低周往复荷载作用下进行试验，试验结果表明该体系抗侧刚度、极限承载能力和延性均优于普通钢框架体系.其次，目前对于填充墙钢框架的有限元模拟方法不尽相同［4－9］，针对带围护墙板钢框架的数值模拟仍较少.

采用有限元软件ANSYS建立内嵌围护墙板钢框架的精细化模型，在与已有试验结果进行对比分析的基础上，进行内嵌围护墙板钢框架抗侧力性能分析，最终给出各种因素对围护墙板钢框架侧向刚度和承载能力的影响规律及量化指标.

1 精细化模型

1.1 墙板节点模型

在进行整体结构建模时，墙板与框架之间连接的准确模拟至关重要.由于钩头螺栓连接(图1)在实际工程中使用较多，因此在整体建模时利用弹簧单元来模拟钩头螺栓节点.采用有限元模拟获得螺栓刚度，结合实际钩头螺栓构造对其进行简化，忽略墙板作用，对螺栓与角钢焊接处节点施加全约束，螺栓与墙板发生变形时相接触部位的节点在侧移方向上进行耦合，保证变形的协调性.施加侧向均布荷载.得到钩头螺栓的刚度曲线见图2.由曲线可确定螺栓初始刚度为12.9 kN/mm.

图1 实际钩头螺栓模型

图2 钩头螺栓荷载－位移曲线

1.2 整体结构模型

框架模型尺寸选取与文献［2］中试验模型保持一致.模型各部分模拟单元见表1.Solid65为ANSYS中模拟混凝土的专用单元，该单元考虑了混凝土材料非线性、开裂、压溃等特性，能够较好地考察框架节点局部应力变化以及墙板与框架之间的接触模拟，框架采用Solid95单元.墙板采用分块墙板，宽度为600 mm，厚度为100 mm，材料本构选用轻质混凝土本构模型［10］，配筋采用整体式配筋，混凝土破坏准则为五参数破坏准则.混凝土闭合裂缝剪应力传递系数取0.9，开裂剪应力传递系数取0.5.为了保证计算收敛，仅考虑混凝土受拉开裂而不考虑其压溃，当墙板拉应力达到0.4 MPa即开裂.通过定义接触单元参数最大摩擦应力(1 MPa)来模拟墙体之间的粘结作用，接触面法向罚刚度因子取10［11］，墙板节点采用弹簧单元来模拟.

表1 选用单元

对模型上下层施加大小相等的单调荷载，分析结果与试验结果对比见图3，结果表明，采用该计算模型的结构荷载－位移曲线与试验结果基本吻合.对照曲线与空框架极限荷载作用下的应力云图(图4)可以看出，空框架在顶点位移30 mm以内，水平力＜100 kN时，框架变形保持在弹性范围内，当顶点位移超过30 mm时，框架刚度出现突变，刚度接近于零.对带墙板框架，同样是在顶点相同位移时发生刚度突变，原因是在相同位移处，框架节点进入塑性，此后结构刚度主要通过墙板与框架之间的协同作用来贡献，墙板的存在不致于使结构像空框架一样刚度突变接近于零，从而使结构具有继续承载的能力.

图3 数值模拟结果与试验结果对比

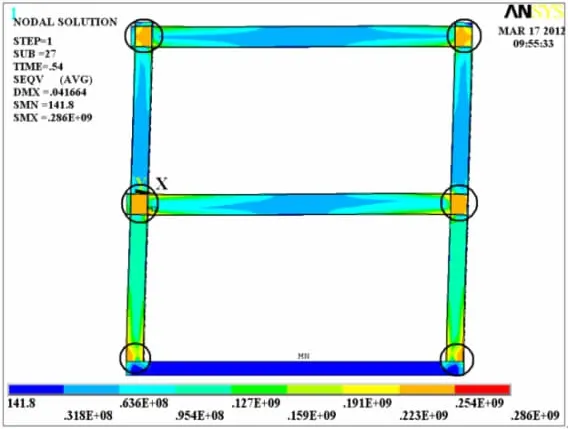
图4 侧向荷载为120 kN时空框架应力云图

带墙板框架变形和受力过程总结:初始受力阶段，墙板主要是通过连接节点与框架协同变形，框架初始刚度的增加主要由墙板与框架的协同工作来实现.在较小荷载下(130 kN)，节点连接处墙板首先出现裂缝，图5所示侧向荷载为130 kN时墙板裂缝图，之后由于墙板和框架的变形，墙板对角分别与框架上下梁翼缘顶紧，框架继续变形时墙板节点力不再继续增大，节点处的裂缝不会继续扩展，此时框架主要通过墙板的对角顶紧进行传力，图6所示侧向荷载为210 kN时墙板应力云图，可以看出应力呈对角分布模式，之后墙板角部逐渐出现裂缝并且一步步沿对角线扩展.

图5 侧向荷载为130 kN时墙板裂缝图

图6 侧向荷载为210 kN时墙板应力分布云图

2 参数分析

以相关建筑设计标准和抗震规范为依据进行参数化设计，分别选取轴压比、跨度、墙板宽度、墙板厚度及墙体开洞形式及面积为参数，针对每种参数进行模型设计和分析，总结分析计算结果，发现规律，指导实践运用.

2.1 轴压比

选取柱轴压比分别为 0、0.1、0.3、0.5、0.6 五种情况进行分析.框架层高取3 m，跨度取4.5 m.文中仅选取轴压比为0、0.3和0.5情况结果对比.图7所示为各轴压比下有无墙体钢框架荷载－位移曲线，可以看出，竖向荷载对空框架的初始刚度影响较小，但对其极限荷载影响较大，原因是空框架的破坏是由节点全面进入塑形而导致整体结构失效.在竖向荷载的作用下，框架节点会提前进入塑形阶段，因此轴压比越大，空框架侧向承载力越小.极限荷载定义为一层层间位移角达到1/50时的荷载，荷载－位移曲线中位移取值为二层层顶位移.

图7 各轴压比下有无墙体钢框架荷载－位移曲线

对于带墙板框架在不同轴压比作用下其极限荷载相差较小，原因是在框架发生一定的变形时，墙板与框架对角顶紧，带墙板框架的极限承载力主要由墙板决定.由图7可以看出，随着轴压比的增大，带墙板框架的侧向初始刚度不断增大，这是因为在竖向荷载作用下，墙板与梁之间压力增大，从而导致在整体结构发生侧向变形时摩擦阻力增大，使框架侧向刚度增大.计算结果见表2，可以看出，当轴压比为0.6时，带墙板框架刚度和承载力增大系数都超过了2.0.

表2 不同轴压比计算结果

为了分析轴压比变化时对结构抗震性能的影响，分别取轴压比为0.5和0两种情况对结构进行滞回分析.施加水平荷载为150 kN的往复荷载.图8所示为不同轴压比下带墙板钢框架滞回曲线，可以看出，在没有竖向荷载时，结构的滞回曲线呈反S形并具有“捏缩”效应，反映了更多的滑移影响.而轴压比为0.5时，结构滞回曲线大致呈梭形，反映了整个结构较强的塑性变形能力和耗能能力，原因是竖向荷载的存在减小了墙板与框架之间的滑移现象并且使墙板更多参与了结构的耗能.

图8 不同轴压比下带墙板钢框架滞回曲线

2.2 跨高比

框架层高取3 m，跨度分别取5.7、5.1、4.5、3.9、3.3 m.首先对空框架进行分析(柱轴压比取0.5)，对于空框架，在层高不变只改变跨度的情况下其刚度和极限荷载变化较小，原因是框架的刚度主要由柱的刚度决定.图9所示为不同跨高比情况下带墙板钢框架刚度曲线，可以看出，对于带墙板框架，随着跨度的增大，墙板数量也随之增多，带墙板钢框架的刚度及极限承载力都随之提高.计算结果见表3，可以看出，随着跨高比的减小，刚度增大系数和极限承载力增大系数基本呈线性变化，跨度对带墙板框架的极限承载力影响更大.

图9 不同跨高比下带墙板钢框架刚度曲线

表3 不同跨高比计算结果

取跨度为4.5 m和5.7 m两种情况，同样对框架施加水平荷载为150 kN的往复荷载，图10所示为不同跨度及墙板宽度情况下钢框架滞回曲线，可以看出，由于跨度较小时，墙板数量较少导致刚度较小，在相同荷载作用下结构较早的通过发展塑性来耗能，因此跨度较小时滞回曲线比较饱满，而跨度较大时结构大部分仍处于弹性阶段.

图10 不同跨度及墙板宽度下钢框架滞回曲线

2.3 墙板宽度

根据目前工程中实际运用的几种板材规格［12］，分别取墙板宽度为 300、420、520、600、700 mm.框架层高同样为3 m，跨度为4.5 m，轴压比取0.5.图11所示为内嵌不同宽度墙板钢框架荷载－位移曲线，可以看出，随着墙板宽度的增加，带墙体框架的初始刚度及极限荷载都有所增加.当墙板宽度为300 mm(侧向荷载150 kN)时，单片墙板的刚度较小，所以主要通过墙板之间的相互作用来进行力的传递(图12(a))，在墙板中形成两条传力主线，另外，墙板宽度较小时，当框架发生侧向变形时会有更多的面发生错动，整体性较差，因此降低了整体结构的刚度.而当墙板宽度较大时(如700 mm)，单块墙板刚度较大，当框架发生变形时，墙板主要通过单块墙板对角顶紧来传力(图12(b))，并且墙板错动面较少，墙板整体性较好，因此随着墙板宽度的增大，结构整体侧向刚度随之提高，并且极限承载力也有所提升.不同墙板宽度计算结果见表4，可以看出，当墙板宽度为700 mm(侧向荷载220 kN)时，初始刚度及承载力增大系数都达到2.0以上.

表4 不同墙板宽度计算结果

图11 内嵌不同宽度墙板钢框架荷载－位移曲线

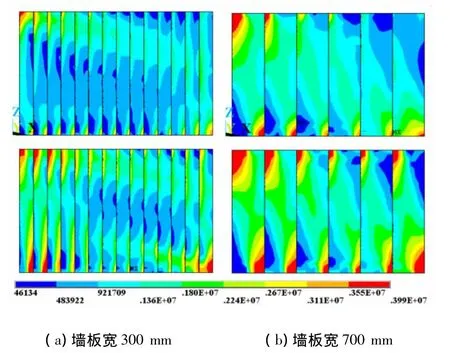
图12 不同墙板宽度墙板应力云图

墙板宽为300 mm和600 mm时框架的滞回性能在图10中也有所体现，可以看出，两种宽度的墙板下框架的滞回性能差距较大，墙板宽度为300 mm时，在相同荷载作用下框架的滞回曲线呈饱满的梭形，原因是结构通过较大程度的发展塑形来进行耗能.

2.4 墙板厚度

分别取墙板厚度为 75、100、125、150 mm，框架高度为3 m，跨度为4.5 m，轴压比为0.5，墙板宽度为600 mm.图13所示为内嵌不同厚度墙板钢框架荷载－位移曲线，可以看出，随着墙板厚度的增大，带墙体框架的初始刚度及极限荷载都有所增加，原因是当墙板厚度增大时，单块墙板的刚度随之增大，对角传力效应更加明显.计算结果见表5，当墙板厚度为150 mm时，带墙板框架初始刚度及极限承载力增大系数在2.5左右，墙板对结构的影响不能忽略，当不同地区采用不同厚度墙板时应采用不同的刚度及极限承载力增大系数.

表5 不同墙板厚度计算结果

图13 内嵌不同厚度墙板钢框架荷载－位移曲线

墙板厚度为75 mm和100 mm时框架的滞回曲线见图14，可以看出，墙板厚度为75 mm时，在相同荷载作用下框架的滞回曲线比较饱满，原因与墙板宽度较窄时相似，结构通过较大程度的发展塑形来进行耗能.

图14 不同墙板厚度下钢框架滞回曲线

2.5 开洞形式及面积

以相关建筑规程为依据在原模型(层高3 m，跨度4.5 m，轴压比0.5，墙板宽600 mm)基础上建立带门洞和窗洞8个模型，洞口布置及尺寸见图15及表6，前4种模型为门洞模型，后4种模型为窗洞模型.

图15 洞口布置形式

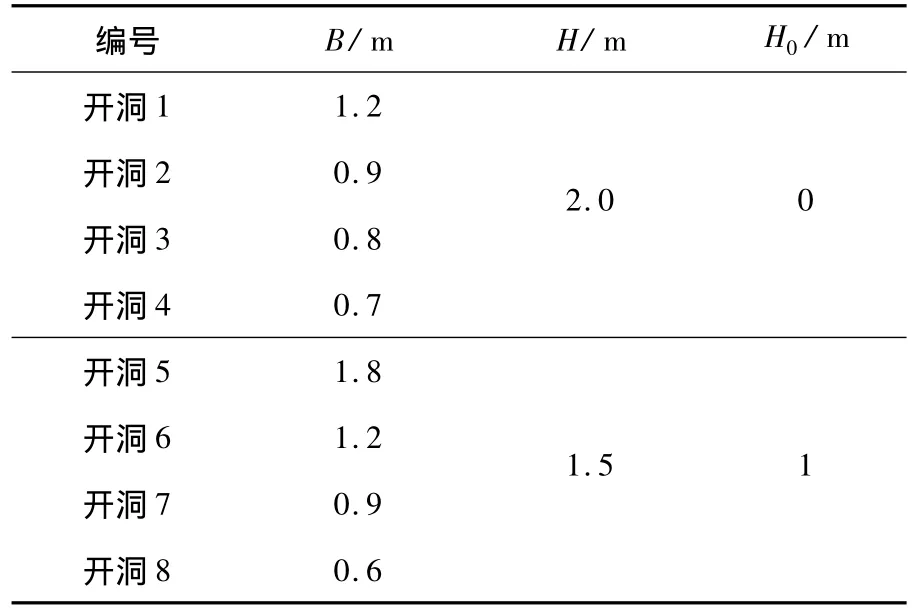
表6 洞口尺寸

图16所示为带门洞框架荷载－位移曲线，可以看出，对于门洞(开洞1～4)，其承载力和初始刚度基本一致，原因是4种情况下洞口均位于框架中部，并且最大宽度和最小宽度差距较小，洞口仅对中部两块墙板的完整性造成了破坏，而当框架发生变形使墙板对角顶紧时，主要受力部位为靠近框架柱的两块墙板，对于承载力和刚度的贡献也主要来自这两块墙板，图17(a)所示为开洞1模型的墙板应力云图，可以看出，靠近柱的两块墙板应力较大.窗洞(开洞5～8)情况与带门洞框架相似.

图16 带门洞框架荷载－位移曲线

以上均是在完整的墙板上直接开洞后进行分析，因此在开洞情况下其承载力和刚度必然会有所降低.而实际工程中均需对洞口进行加固.鉴于此，本文在已有洞口的基础上选取与实际工程中相同的角钢对洞口周边进行加固.建模时，在洞口四边用梁单元来模拟角钢，模型中采用耦合3个方向自由度的方法来模拟墙板与角钢间的铆钉连接.加固后的墙体由于角钢的存在较大程度限制了墙体的变形和裂缝的提早出现，由图17(b)可以看出，墙板传力路径发生明显变化，墙板应力集中部位由洞口角部转移到了离洞口较远的墙板上，洞口周边墙板产生了较大应力.图18所示为洞口加固前后钢框架荷载－位移曲线，可以看出，洞口加固后结构承载力和刚度都有较大提高，与不开洞的情况相近.因此，在工程设计时，对于位于框架中部并且尺寸较小的加固洞口可不考虑洞口对整体结构刚度和承载力的削弱作用.

图17 开洞1加固前后墙板应力云图

图18 洞口加固前后钢框架荷载－位移曲线

3 结论

1)对于内嵌围护墙体钢框架协同作用分析的有限元模型，钢框架采用实体单元，墙板采用混凝土单元，墙板节点采用弹簧单元，墙体与框架之间的相互作用采用接触单元可有效模拟实际结构的受力性能.

2)当轴压比从0增大到0.6时，空框架极限承载力减小30%左右.但对带墙体钢框架极限承载力的影响可以忽略.设计过程中若考虑围护墙体的作用，则对于不同大小的竖向荷载，应采用不同的侧向刚度增大系数和承载力增大系数进行刚度和承载力调整.

3)对于空框架当层高不变而跨度变化时，侧向刚度和极限承载力基本保持不变.而带墙板钢框架当跨度达到5.7 m时，侧向刚度及承载力增大系数可达到2.0以上.设计过程中应根据不同跨度采用不同的增大系数.

4)所采用的分块墙板宽度越大，其对钢框架的侧向刚度及承载力贡献越多.建议工程优先选用600 mm宽墙板，对结构刚度及承载力的影响适中.

5)当墙板厚度大于100 mm时，带墙板钢框架侧向刚度及承载力增大系数均达到2.0以上，不同地区选用不同厚度墙板时，应采用不同大小的增大系数.

6)位于框架中间位置不同尺寸的洞口当其对墙板完整性破坏程度相当时，洞口对整体结构的刚度及承载力削弱程度相近.位于框架中部且尺寸较小的墙体洞口进行加固后洞口对框架整体刚度及承载力影响较小，设计时可不考虑洞口的影响.

［1］金晓飞，孙建云.国内钢结构住宅现状调研［J］.钢结构进展与市场，2011，4(9):50－53.

［2］李国强，王城.外挂式和内嵌式ALC墙板钢框架结构的滞回性能试验研究［J］.钢结构，2005，20(1):52－55.

［3］许刚.镶嵌式填充墙钢框架抗侧力性能试验研究［D］.天津:天津大学，2007.

［4］侯和涛，邱灿星，李国强.钢框架结构与墙体(板)共同作用研究［J］.钢结构，2010，25(4):25－28.

［5］TASNIMI A A，MOHEBKHAH A.Investigation on the behavior of brick-infilled steel frames with openings，experimental and analytical approaches ［J］.Engineering Structures，2011，33(3):968 －980.

［6］KAYMAK F，TUNA M.Investigation of the behaviour of steel frames with the partial and full infill walls under horizontal loads with elasto-plastic methods［J］.Journal of the Faculty of Engineering and Architecture of Gazi University.2011，26(2):435 －445

［7］张容，吴芸.空腔砌块复合墙体钢框架的刚度分析［J］.国外建材科技，2003，24(5):85 －87.

［8］李国华，郁银泉，顾强.钢框架内填混凝土墙结构体系有限元分析［J］.四川建筑科学研究，2007，33(S):17－20.

［9］戴绍斌，余欢，黄俊.填充墙与钢框架协同工作性能非线性分析［J］.地震工程与工程振动，2005，25(3):25－28.

［10］颜雪洲.轻质高性能混凝土力学性能试验研究及新型复合墙体性能分析［D］.北京:北京交通大学，2006.

［11］田海，陈以一.ALC板材抗剪性能系列试验研究［C］//第14届全国结构工程学术会议论文集.北京:工程力学，2005:417－423.

［12］中国建筑标准设计研究院.03SG715—1蒸压轻质加气混凝土板困(NALC)构造详图［S］.北京:中国建筑标准设计研究院，2003.