基于模拟退火遗传算法的GMDH网络模型
张 慧,刘湘南,黄 刚
(1.天津城市建设学院计算机与信息工程学院,天津300384;2.中国地质大学(北京)信息工程学院,北京100083;3.91917部队信息中心,北京100841)
GMDH网络源于GMDH方法[1],它是通过递阶自由分层动态构造的多项式神经网络.GMDH网络建模时网络结构是在训练中动态确定,而不需要知道输入输出变量之间的先验知识.这种方法可以依据提供的较少的系统信息,通过自组织的模型结构,建立不同建模目的模型,适应不同的复杂系统.文献表明,GMDH网络在复杂系统建模、多目标优化、预测等方面有广泛的应用[2-5].但是GMDH网络在建模过程中,一般采用最小二乘法来辨识多项式系数,由于使用最小二乘法来辨识参数存在局限性,传统的GMDH网络在应用时往往需要改进,许多学者在致力于改进传统GMDH网络辨识方法的研究[6-8].
遗传算法作为一种全局优化算法,成功运用于系统辨识与参数优化[9].但同时遗传算法在全局搜索中存在早熟问题,不能保证收敛于全局最优点[7].为避免落入局部最优,模拟退火算法采用Metropolis接受准则,最终渐近收敛于全局最优解[10].本文在GMDH网络中,将模拟退火算法与遗传算法结合起来用于对二元二次多项式系数的辨识和优化,建立了基于模拟退火遗传算法的GMDH网络模型,并将模型应用于泥石流的预测.计算机仿真结果表明,本文建立的模型是有效的.
1 GMDH网络
1.1 GMDH基本原理
假定系统S有m个输入变量xi(i=1,2,…,m),有一个(一般情况下可能多个)输出变量y.现在的问题是如何确定下面非线性函数f(·)的显明式子:

其中,函数f可以一般的展成离散型Volterra多项式级数(K-G多项式)[6]:

其中,a0,ai,aij,aijk,…,(i,j,k=1,2,…,m)为多项式系数.
(2)式被广泛用来作为非线性模型的完全描述.但要完全确定a0,ai,aij,…等参数的值是不现实的,因为输入变量增多,(2)式的项数就会急剧加大.GMDH网络模型是通过多层筛选的方法,用局部简单的模型不断组合逼近(2)式,以得到整体上比较复杂的模型.
1.2 GMDH网络的结构
典型的GMDH网络结构图如图1所示.

图1 GMDH的网络结构图Fig.1 The structure of GMDH network
GMDH网络的层数和单元连接并不固定,图1为示意图,实际的GMDH网络通过自组织的形式建立.GMDH的处理单元是一种双输入单输出的结构.输入和输出之间的关系以完全二元二次多项式来表示:

其中,a,b,c,d,e,f为完全二元二次多项式系数.
在GMDH网络结构中,处理单元由相邻两层的神经元组成.处理单元的输入来自上层的两个神经元,两个神经元形成的完全二元二次多项式作为处理单元的输出,也就是下层的神经元.网络每递进一层,多项式的次数递增2阶,最终整个网络可以形成2k阶多项式(k为GMDH的层数).由此可见,GMDH网络是能够表达离散型Volterra多项式级数(K-G多项式)的结构模型.
1.3 模拟退火遗传算法用于辨识多项式的系数
(3)式中系数a,b,c,d,e,f的辨识通常是用最小二乘法.由于最小二乘法在参数辨识时具有容易陷入局部最小、辩识非线性系统能力差以及不适用于严重干扰的情况等不足[9],因而传统的GMDH网络在应用中效果不理想.遗传算法作为一种全局优化算法,成功运用于系统辨识与参数优化.但是遗传算法在全局搜索中也存在早熟问题,不能保证收敛于全局最优点[10].为避免落入局部最优,模拟退火算法采用Metropolis接受准则,最终渐近收敛于全局最优解[11].将模拟退火算法与遗传算法结合起来用于对参数的辨识和优化,既保证了全局寻优又防止了过早收敛,进一步提高了全局与局部寻优能力.
2 基于模拟退火遗传算法的GMDH网络模型
2.1 模拟退火遗传算法的流程
遗传算法是先将优化问题的一组基本可行解(xi,yi,zi)编码为一组二进制的字符串即染色体,再对这些染色体进行复制、交换和变异等操作,从而实现参数的优化.
运用模拟退火遗传算法辨识多项式(3)的系数a,b,c,d,e,f,流程如下图2所示:
对遗传交叉操作的结果进行模拟退火操作,根据Metropolis准则判断是否接受交叉操作所得到的新染色体;对变异操作所得结果进行模拟退火操作,根据Metropolis准则判断是否接受变异操作所得到的新染色体;并利用Tl+1=αTl对算法进行降温操作.从而实现遗传算法与模拟退火算法的结合,以达到寻优目的.
2.2 基于模拟退火遗传算法的GMDH网络的建模
GMDH网络进行预测,要根据样本,通过自组织的方法建立网络模型.建立GMDH模型需要以下几个步骤:
步骤1:数据收集并把数据分成两个子集:训练集和测试集.在总数为n的数据样本中取出n1个样本作为建摸样本(n1<n),GMDH网络的输入数据形如[x1,x2,…,xm,Y],是多输入变量单输出变量的结构;
步骤2:构建基本单元.将样本的m个变量中任取两个xi,xj(i,j=1,2,3,…,m,i≠j),以Y为输出,用模拟退火遗传算法辨识部分描述式(3)中的参数a,b,c,d,e,f,这样可以得到m·(m-1)/2个基本单元,从而产生第1层,构成初始的网络;

图2 模拟退火遗传算法流程图Fig.2 The flow chart of the SA-GA algorithm
步骤3:建立输入层.先设定一个阈值Eg(Eg的设置需要一定的先验知识,在本文中将Eg设为当前所有单元输出方差的均值,这样在第一步的处理中就可以将误差较大的单元剔除),将余下的n2个样本(n2=n-n1)中的相应变量分别代入上述处理单元,算出处理单元的输出与实际输出的方差E,将各单元的方差与Eg比较,保留那些方差低于阈值的单元(设共有u1个单元),记录这些单元中的最小方差E1m.这样就得到了第一层的单元;
步骤4:构筑中间层.将全部数据中的相应变量代入第一层单元进行计算,得到第一层的输出Y1(u),(u=1,2,…,u1),将Y1(u)作为第二层的输入,重复上述两步,可以得到第二层的处理单元u2个,第二层的输出Y2(u),(u=1,2,…,u2),以及第二层的最小方差E2m,),如果E2m〈E1m,则第二层构筑成功,继续进行下一层的构造;
步骤5:建立输出层.假设进行到第k+1层,发现该层的最小方差Ek+1m>Ekm,则终止建模,并将第k层中方差最小的那个单元作为输出单元.
最后,将与输出单元相关的上层单元逐层连接,这样,其余的无关单元不包含在网络结构中,至此,得到了以样本为基础的GMDH网络.将相应的测试样本输入网络模型,就可以进行预测了.
3 基于模拟退火遗传算法的GMDH网络模型预测泥石流建模实例
泥石流是复杂的非线性系统,利用非线性理论对泥石流预测预报是可行的[12].用人工神经网络的非线性结构来进行建模和预测,是解决复杂的非线性映射问题的有效方法.本文将基于模拟退火遗传算法的GMDH网络模型(SAGA-GMDH)用于泥石流的预测.以泥石流一次最大冲出量(Y)为输出神经元,以流域面积(x1)、流域相对高差(x2)、补给段长度比(x3)、河沟纵坡(x4)、植被覆盖率(x5)、沟岸山坡坡度(x6)、24 h最大降雨量(x7)和人口密度(x8)8个因子为输入神经元,建立泥石流一次最大冲出量预测模型.变量及原始数据来源于文献[13].采用文献[13]中前30组泥石流沟的数据作为建模样本数据,用已训练好的模型对后9组泥石流沟的一次最大冲出量进行预测.
现将GMDH网络结构、SAGA-GMDH网络结构对泥石流沟的一次最大冲出量进行计算机仿真.

测节点数).通过计算机仿真得到预测结果如图3、图4所示.
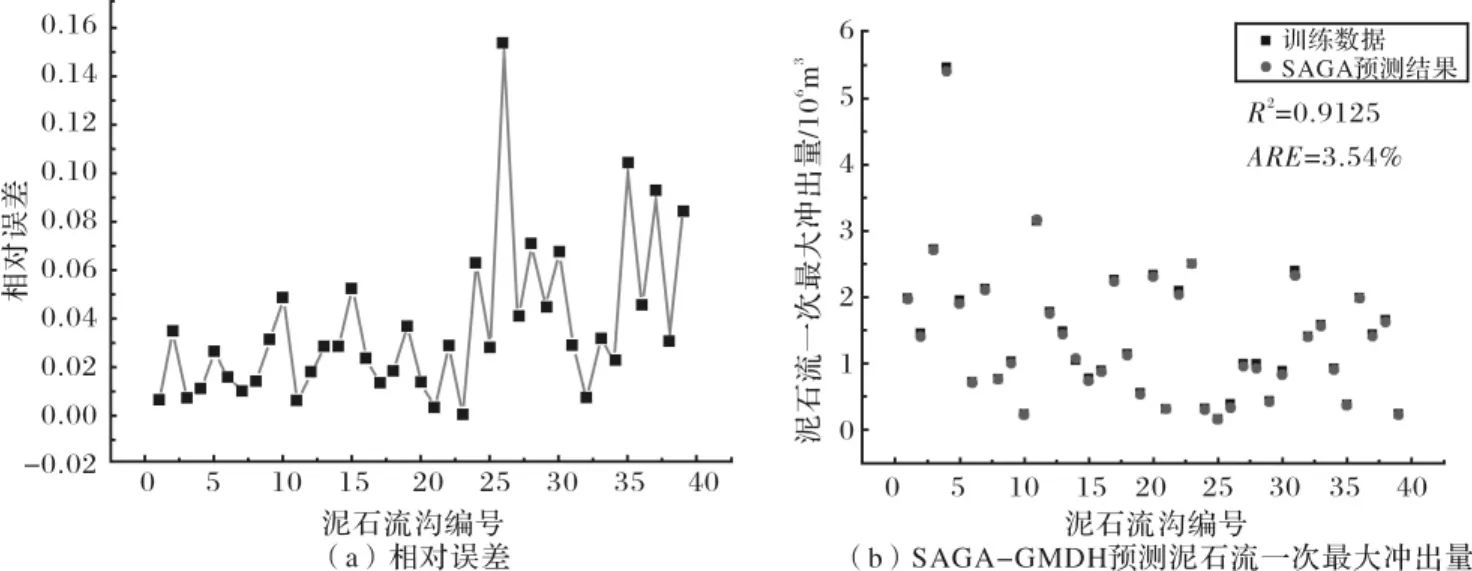
图3 SAGA-GMDH预测的相对误差及泥石流一次最大冲出量Fig.3 The relative error(RE)and results of the SAGA-GMDH model for predicting the BQDR(biggest quantity debris flow rushing out once a time)
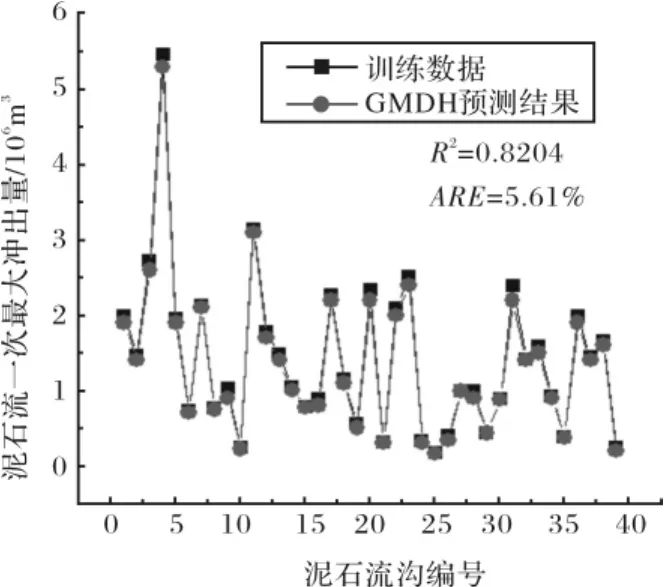
图4 GMDH预测泥石流一次最大冲出量Fig.4 Results of the GMDH model for predicting the BQDR
利用SAGA-GMDH网络进行预测,平均相对误差为3.54%,相关系数为0.912 5.优于GMDH网络模型的预测结果,其平均相对误差为5.61%,相关系数为0.820 4.
4 结束语
针对遗传算法全局搜索能力强,但局部搜索能力较差,而模拟退火算法局部搜索能力较强的特点,将模拟退火算法与遗传算法相结合应用于辨识GMDH网络部分描述式系数,从而克服了传统GMDH网络建模用最小二乘法辨识参数时常常陷入局部极小导致模型预测效果不理想的问题.通过泥石流数据仿真试验,证明了本文提出的基于模拟退火遗传算法的GMDH模型对泥石流预测分析是可行的,而且可以得到较好的预测模型.由于GMDH方法具有较大的灵活性,适用于解决复杂系统的实际问题.
[1] Ivakhnenko A G,Ivakhnenko G A.The review of problems solvable by algorithms of the group method of data handling[J].Pattern Recognition and Image Analysis,1995,5(4):527-535.
[2] Safikhania H,Hajiloo A,Ranjbar M A.Modeling and multiobjective optimization of cyclone separators using CFD and genetic algorithms[J].Computers and Chemical Engineering,2011,35:1064-1071.
[3] 吴耿峰,彭 虎.具有混沌特征的GMDH网络在降雨量预测中的应用[J].小型微型计算机系统,2000,21(2):135-137.
[4] Xiao J,He C,Jiang X.Structure identification of Bayesian classifiers based on GMDH[J].Knowledge-Based Systems,2009,22(6):461-470.
[5] Madandoust R,Bungey J H,Ghayidel R.Prediction of the concrete compressive strength by means of core testing using GMDH-type neural network and ANFIS models[J].Computational Materials Science,2011,51(1):261-272.
[6] Heung S H.Fuzzy GMDH-type neural network model and its application to forecasting of mobile communication[J].Computers &Industrial Engineering,2006,50:450-457.
[7] Hernandez F,Herrera F.Intelligent identification of a fermentative process using modified GMDH algorithm[J].Revista Iberoamericana De Automatica E Informatica Industrial,2012,9(1):3-13.
[8] 陈 洪,陈森发.基于遗传算法的GMDH网络模型及其应用[J].数据采集与处理,2009,24(6):820-824.
[9] 陈森发.复杂系统建模理论与方法[M].南京:东南大学出版社,2005.
[10] 刘 勇,康立山,陈毓屏.非数值并行算法(第二册)遗传算法[M].北京:科学出版社,2003.
[11] 王雪梅,王义和.模拟退火算法与遗传算法的结合[J].计算机学报,1997,20(4):381-384.
[12] 孟凡奇.基于GIS的泥石流预测预报[D].长春:吉林大学,2011:97-98.
[13] 金 鑫.鞍山市岫岩县泥石流危险性评价研究[D].长春:吉林大学,2011:44-46.
- 华中师范大学学报(自然科学版)的其它文章
- Google Earth影像与同源Quick Bird影像在城市土地利用分类上的对比研究

