基于ESDA的深圳市住宅基准地价空间分布规律研究
任 慧
(1.广东省国土资源测绘院,广东 广州 510500)
深圳市从2009年12月1日开始实施“城市更新”。研究全市住宅基准地价分布规律,对制定特区内外价格调控机制、城市更新拆迁补偿政策及确定法定图则基准容积率等具有重要意义。目前国内外学者在地价方面已进行大量研究,但研究方法单一,且因采集样本不均匀和数量有限,预测结果可信度不高[1-4]。地理统计学的探索性空间分析已逐渐在社会经济领域得到越来越广泛的应用[5-16]。笔者应用GIS探索性空间分析方法,以最新公告的深圳市住宅基准地价样点为基础数据,探索了特区内外住宅基准地价的空间分布规律。
1 GIS探索性空间分析原理
探索性空间分析(ESDA)是在一组空间数据中寻求重要信息的过程,利用ESDA技术,直接探索隐藏在数据中的关系、模式和趋势等,获得对问题的理解和相关知识。ESDA是建立在一定假设基础上的[17],其具体思路为先分离出数据的模式和特点,再根据数据特点选择合适的模型。插值结果可靠性检验以假设条件为前提,故插值前须进行空间数据的探索性分析,包括对空间数据进行数据结构分析、趋势分析、方向分析、步长分析及离群值查找等检验。
2 实证研究
2.1 研究数据的来源
数据来源于深圳市国土资源和房产管理局于2006年5月公告的《深圳市住宅用地公告基准地价》,包括南山、福田、罗湖和盐田4区,以及坂田、布吉、大浪、大鹏、福永、公明、观澜、光明、横岗、坑梓、葵涌、龙城、龙岗、龙华、民治、南澳、南湾、平湖、坪地、坪山、沙井、石岩、松岗、西乡和新安25个街道,共采集32 538个样点。
2.2 基于ESDA住宅基准地价模型构建
2.2.1 数据检验
1)空间格局检验。空间格局分析方法可以发现某类事物在空间上是集聚还是发散,或是随机。不同尺度下,点状地物的分布模式各异,应用密度分析方法可以发现在不同尺度下空间数据分布规律,如图1所示。
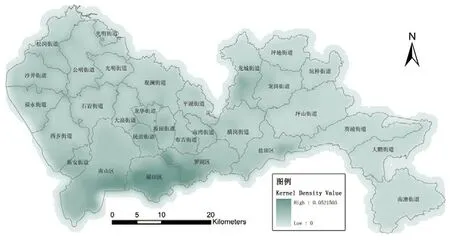
图1 密度分析图
2)数据分布检验。样点数据未变换前,数据高度偏斜,不符合正态分布;经对数变换后,样点数据的标准QQPlot图整体分布点基本沿普通QQPlot图直线对称,变换后数据近似正态分布,如图2所示。
3)趋势分析检验。趋势分析结果显示,研究区的样点地价至少存在二价函数趋势,东西向表现为中间高两尾低的“凸形”趋势,南北向表现为自北向南逐渐递增且斜率逐渐增大的趋势。
4)步长和分组检验。通过距离分析发现,样点对之间的最大距离为92 400 m。因此,以2 310 m为步长,步长组数为20,满足公式:步长×步长组数×2=样点对间的最大距离。为验证步长分组的合理性,后面将对样点数据进行不同步长的插值,以比较不同步长下的插值误差。
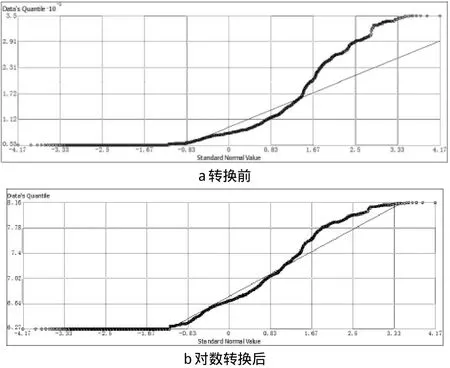
图2 深圳市住宅基准地价样点QQPlot分布图
5)离群值检验。经直方图法离群值查找,发现坪山街道、大鹏街道、南澳街道、葵涌街道地价普遍较低,因所采用样点为真实的地价数据,故对离群值不予处理,见图3。
2.2.2 插值模型选择及误差监测
地统计学中,空间插值预测结果的误差可从无偏性估计、均方根误差和均方根标准误差3个角度分析。误差预测方法简化后,选择标准化误差和均方根标准误差来判断插值模型优劣。标准化误差趋于零,均方根标准误差趋于1,插值结果的可信度越高,插值模型越好,反之,模型不理想。
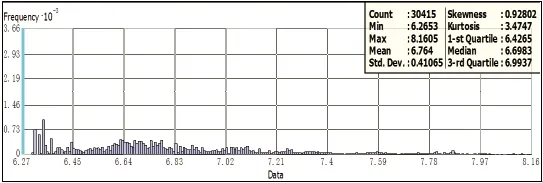
图3 直方图法离群值检验(对数变换后)
地统计插值法利用已知样点的统计特性,不但能量化已知点之间的空间自相关性,而且能解释采样点在预测区域范围内的空间分布状况,代表模型是克里格模型。普通克里格方法因其独特的灵活性而广泛应用于空间数据预测。克里格模型基于以下假设:所有随机误差都具有二级平稳性,即随机误差的均值为零,且任意2个随机误差之间的协方差只与两者之间的距离和方向有关,而与它们的具体位置无关;普通克里格方法要求数据必须为正态分布。不同插值模型比较如表1所示。
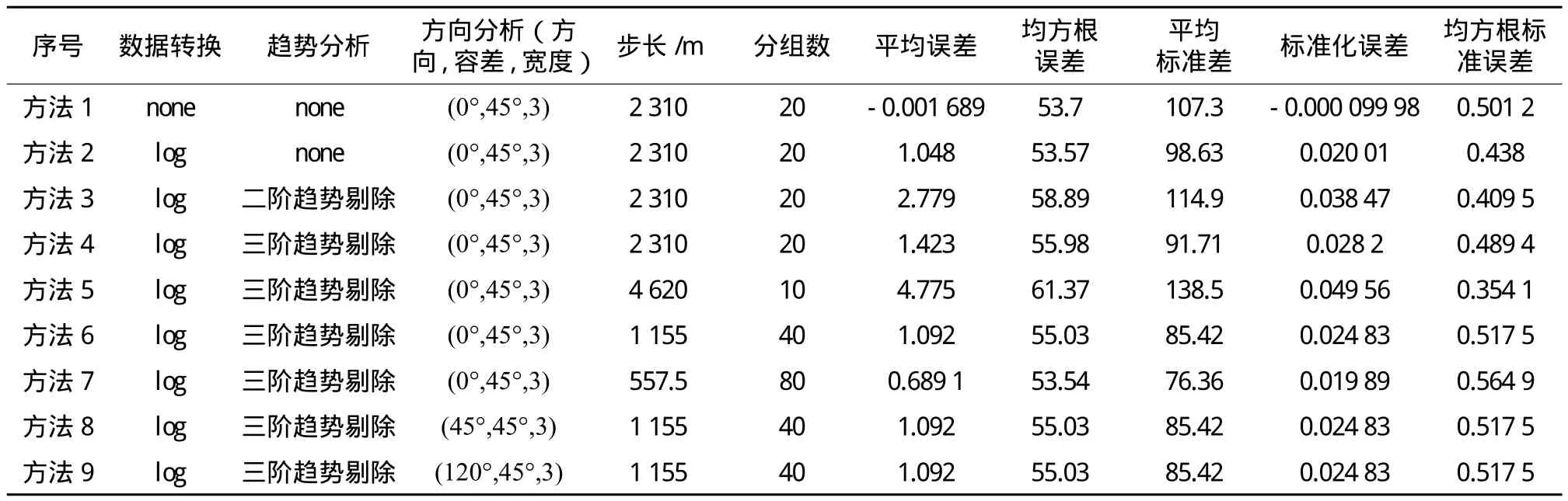
表1 不同插值模型参数及误差监测结果
由表1可知,转换前的原数据(方法1)QQPlot图不趋于一条直线(见图2),标准化误差为-0.000 099 98,均方根标准误差为0.501 2,模型变异性被夸大,原数据不呈正态分布,不满足克里格插值的条件。对数转换后的样点(方法2)近似呈正态分布(见图2),标准化误差为0.020 01,均方根标准误差为0.438。可见,对数转换后,模型变异性相对较小,插值效果较理想。趋势分析表明,研究区样点至少存在二价函数趋势,经对数转换和二阶趋势剔除后(方法3),标准化误差为0.038 47,均方根标准误差为0.409 5,而三阶趋势剔除后(方法4),标准化误差为0.028 2,均方根标准误差为0.489 4,表明三阶趋势剔除后插值效果较理想。方法4~方法7步长分别为2 310 m、4 620 m、1 150 m和557.5 m情形,标准化误差和均方根标准误差结果表明,方法6插值效果较理想。方法6、8、9为不同方向角度插值情况, 3种插值效果一样,说明方向分析对样点数据插值影响较小。综上所述,方法6为最佳插值模型。
2.3 深圳市住宅基准地价分布规律分析
选择方法6构建地价模型,以100元/m2为间距提取得到住宅基准地价等值线如图4所示。密度分析结果(见图1)显示,研究区样点数据存在局域集聚特征,为进一步准确得到地价集聚类型和空间位置分布,应用热点分析法得到住宅基准地价等值线集聚分布结果。热点分析用GiZScore值来检验空间自相关的统计显著性,正值说明存在高/高集聚,负值说明存在低/低集聚。笔者将32 538个住宅基准地价样点的热点分析结果分类如下:GiZScore>7,定义为高/高集聚区,占样本容量4.67%;0 图4 深圳市住宅基准地价等值线图 图5 深圳市住宅基准地价等值线集聚分布图 研究区样点地价东西向表现为中间高两尾低的“凸形”趋势,南北向表现为自北向南逐渐递增且斜率逐渐增大的趋势。高/高集聚区基本以2 000元/m2住宅基准地价等值线为分界线,主要位于南山区、福田区和罗湖区。高/低集聚区基本以1 000元/m2住宅基准地价等值线为分界线,主要位于松岗街道南部、公明街道西部、沙井街道中部、福永街道中部和北部、西乡街道中部和南部、石岩街道中部、新安街道、大浪街道东南部、龙华街道中部和南部、民治街道、南山街道东南部以外区域、平湖街道北部、坂田街道中部和南部、布吉街道中部和南部、福田区西北部、罗湖区中部和东部、南湾街道南部、横岗街道西北耳环西南部、盐田区西南部和东南部、龙城街道中部和南部、龙岗街道西北部。低/低集聚区基本以800元/m2住宅基准地价等值线为分界线,主要位于松岗街道北部、光明街道、公明街道东南和西南部、沙井街道东部、福永街道东南部、石岩街道北部西部和东南部、西乡街道北部和东北部、大浪街道北部和西南部、观澜街道西部和西北部、龙城街道北部、龙岗街道中部和东部、坪山街道、坪地街道、坑梓街道、大鹏街道、葵涌街道、南澳街道。低/高集聚区基本为800~1 000元/m2住宅基准地价等值线间,位于其他区域。福田区莲花北路-彩田路-笋岗西路-华富五街-华富路-深南中路-新洲路围合区形成3 000元/m2住宅基准地价等值线以上主要集聚区域,主要由于深南大道便捷交通和莲花山稀缺景观资源优势所致。 经ESDA分析后,插值模型预测效果明显改善,结合等值线和热点分析方法,可以揭示出住宅基准地价空间分布规律特征。 [1]刘志霞,张加恭,赵永国. 深圳经济特区住宅基准地价空间分布特征与影响要素分析[J]. 华南师范大学学报:自然科学版,2009(2):111-116 [2]鲁成树,吴次芳,白雪华. 小城镇基准地价演变的内在驱动因子分析——以温州市泰顺县为例[J]. 价格理论与实践,2003(2):50 -51 [3]杜德斌,徐建刚. 影响上海市地价空间地价区位因子分析[J].地理学报,1997,52(5):403-510 [4]周瑞平,赵明,张裕凤. 呼和浩特市城市基准地价变化的驱动因子分析[J].干旱区资源与环境,2004,18(9):126-129 [5]丁刚,罗暖. 我国省域科技创新人才队伍建设的现状评价与空间集聚效应研究——基于GPCA模型和ESDA方法[J]. 武汉理工大学学报:社会科学版,2012,25(4):519-525 [6]戈冬梅,姜磊. 基于ESDA方法与空间计量模型的旅游影响因素分析[J]. 热带地理,2012,32(5):561-567 [7]潘竞虎,尹君. 中国省会及以上城市发展效率的DEA-ESDA分析[J]. 西北师范大学学报:自然科学版,2012,48(6):99-104 [8]管伟,陈松林,王之顺. 福建省县域土地利用经济效益空间探索性分析[J]. 福建师范大学学报:自然科学版,2012,28(1):117-124 [9]王晓丹,王伟龙. 广东省区域经济差异的探索性空间数据分析:1990~2009[J].城市发展研究,2011(5):43-48 [10]黄焕春,李明玉. 基于ESDA的长吉图开发先导区城市内部空间结构演化分析——以延吉市为例[J]. 河北师范大学学报:自然科学版,2011,35(6):633-639 [11]陈文成. 基于ESDA的闽西发展不平衡格局动态分析[J]. 地理与地理信息科学,2010,26(2):67-71 [12]程叶青,邓吉祥. 吉林省中部粮食主产区城乡综合发展水平格局特征[J]. 地理学报,2010,65(12):1 591-1 601 [13]王伯礼,张小雷. 新疆公路交通基础设施建设对经济增长的贡献分析[J]. 地理学报,2010,65(12):1 522-1 533 [14]苏方林. H中国省域R&D活动的探索性空间数据分析H[J].广西师范大学学报:哲学社会科学版,2008,44(6):52-56 [15]何江,张馨之. H中国区域人均GDP增长速度的探索性空间数据分析H[J]. 统计与决策,2006(22):72-74 [16]范新生,应龙根. H中国SARS疫情的探索性空间数据分析H[J].地球科学进展,2005,20(3):282-291 [17]李德仁,关泽群. 空间信息系统的集成与实现[M]. 武汉:武汉测绘科技大学出版社,2000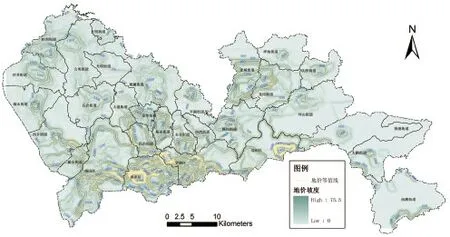
3 结 语

