基于Web服务复杂网络的服务社区构建方法

刘 莹 刘国奇 任介夫 姜琳颖 张 斌

(1东北大学软件学院, 沈阳 110819)

(2东北大学信息科学与工程学院, 沈阳 110819)

互联网上Web服务的数量不断增加,领域也不断扩展,为了有效地管理散落于网络上的Web服务,Web服务社区这一组织形式应运而生[1].基于服务社区进行服务发现、替换,有助于提高服务组合的效率[2].传统的Web服务社区的构建方法是通过用户手动注册实现的,难以对服务资源进行有效的组织和管理.因此,如何自动构建Web服务社区成为服务发现研究中的一个重要方面[3].

本质上,Web服务社区对网络中的服务资源起到分类的作用,而聚类技术可以实现对服务的无指导分类[4].目前广泛使用K-Means算法进行聚类,但该算法在聚类过程中性能依赖于聚类中心的初始位置,而且对孤立点和噪声点数据很敏感.依据Web服务信息,已有的研究采用信息匹配算法将Web服务构建成复杂网络[5],并且验证了该网络具备复杂网络的特性[6].社团结构是复杂网络中广泛存在的一个拓扑属性[7],通过挖掘Web服务复杂网络(Web service network, WSN)中的社团结构,可以有效地自动构建Web服务社区.

传统的复杂网络社团划分算法与计算机科学中的图形分割和社会学中的分级聚类具有密切关系.图形分割算法中常用的2个算法是Kernighan-Lin算法和基于Laplace图特征值的谱平分法[8].Kernighan-Lin算法要求必须事先知道该网络中2个社团的大小,谱平分法主要应用于网络能够近似分为2个社团的情形,这些缺陷导致它们在WSN的分析中难以得到应用.分级聚类算法中最具代表性的是GN算法,其缺陷在于对网络的社团结构没有一个量的定义[8].Radicchi等[9]针对GN算法的这一缺陷提出了自包含GN算法,在计算机生成的随机网络中取得较好的效果,但应用到WSN中,划分出的社团规模分布严重不均,且社团内服务的平均相似度整体偏低.

针对WSN的加权网络特性,本文提出了一种基于加权GN算法的Web服务社区构建方法.首先从语义层面上构建了WSN模型,其中连边的权值等于2个节点所代表的Web服务的输入输出信息的语义相似程度;然后在WSN模型上使用加权GN算法进行社团划分,通过挖掘社团结构实现Web服务社区的自动构建;最后,定义社区内服务相似度模型,对Web服务社区的构建结果进行评价.

1 基于语义相似关系的WSN模型

在基于语义相似关系的WSN模型的建模过程中,首先搜索服务库中可用的Web服务,抽取出这些服务的输入输出信息,并计算这些信息的语义相似程度;其次将Web服务抽象成网络中的节点,将服务之间语义层次的关联关系抽象成边.基于以上描述,本文给出如下定义.

定义1(网络节点(node)) 在基于语义相似关系的WSN模型中,节点是抽象的Web服务,可用五元组表示:

WS=(ID,Porttype,Operation,Message,Description)

(1)

式中,ID是Web服务的唯一标识;Porttype表示特定端口类型的具体协议和数据格式规范;Operation表示对服务所支持的操作的抽象描述;Message表示通信数据的抽象类型化定义;Description表示服务实现功能的描述信息.

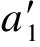
RS(wsA,wsB)

(2)

定义3(网络边(edge)) 设A,B是网络中任意2个节点,若A,B代表的Web服务wsA和wsB满足关系RS(wsA,wsB),则节点A和B间的连线即为网络边.

在构建WSN模型时,通过判定服务输入输出的语义信息是否匹配将不同Web服务建立关联.在构建基于语义相似关系的WSN模型后,需要对模型的网络特性进行度量,具体的度量指标包括:网络的平均路径长度、网络的平均聚类系数、节点的度和度分布.本文通过分析上述特性来分析构建的WSN模型的性质,如果WSN模型满足复杂网络的特征,就可以采用相应的方法进行Web服务社区的构建.

2 基于加权GN算法的社区构建方法

GN算法在社会网等复杂网络中得到了成功应用.但是在本文构建的WSN模型中,节点之间连边的重要性受到节点代表的Web服务的输入输出语义相似程度的影响,该相似程度被定义为网络中的权值.本文将该权值引入到传统GN算法中,改进了算法的删边条件和终止条件,提出了加权边介数和加权强社团的概念,并在此基础上提出了基于加权GN算法的Web服务社区构建方法.

2.1 加权边介数计算

在复杂网络中,社团内部的紧密程度比社团之间的紧密程度要高.原有的GN算法中社团内部的紧密程度通过各节点之间连边的条数计算,在本文提出的WSN模型中,社团内部的紧密程度通过节点的语义相似程度即边的权值计算.为了能够在WSN模型中有效区分一个社团的内部边和连接社团之间的边,本文提出了加权边介数的概念,其表达式如下:

Eweighted=(1-Weight(A,B))Eunweighted

(3)

式中,Eweighted表示加权边介数；Eunweighted表示传统GN算法中的边介数；Weight(A,B)表示节点A和节点B之间连边的权值,它的值等于节点A,B代表的Web服务的语义相似度Sim(A,B).从式(3)可看出,采用本文提出的加权边介数,可以保证边的权值越大(即2个Web服务的相似度越大),得到的边介数越小,从而该边被移除的概率就越小.这样就保证社团内部的节点相似度明显高于不同社团节点的相似度,因而能够满足在基于语义相似关系的WSN模型中构建Web服务社区的需要.

在加权边介数的计算中,最关键的是边的权值即服务相似度的计算.节点A,B的服务相似度(即综合考虑输入输出相似程度)Sim(A,B)定义如下:

Sim(A,B)=w1SimI(A,B)+w2SimO(A,B)

w1+w2=1

(4)

式中,w1和w2分别为输入、输出相似度的权值；输入相似度SimI(A,B)的定义为

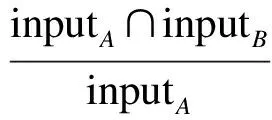
w3+w4=1

(5)

式中,w3表示wsA对输入相似度的影响程度;w4表示wsB对输入相似度的影响程度.

输出相似度SimO(A,B)的定义为

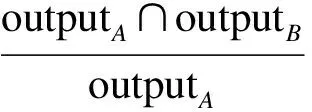
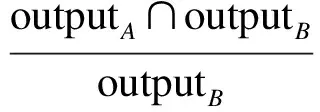
w5+w6=1

(6)

式中,w5表示wsA对输出相似度的影响程度;w6表示wsB对输出相似度的影响程度.在判断参数的语义相似性时,本文采用的是计算概念的语义距离的方法[10].

2.2 加权强社团定义

在传统的自包含GN算法中,Radicchi等[9]提出的强社团结构的定义被用作判断社团划分效果的标准.为了更好地衡量加权WSN中的社团结构,本文改进了强社团定义,将本文构建的WSN模型中的权值和强社团定义相结合,提出了加权强社团的概念,其表达式如下:

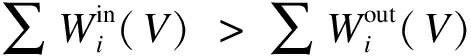
(7)

式(7)的物理意义是:社团V内的任意一个节点i与这个社团内部其他所有节点的连边的权值之和,大于它与该社团外部的所有节点的连边的权值之和.满足该条件的社团V被称为网络中的加权强社团.本文提出的加权GN算法在强社团的概念中引入权值,以便更有效地将Web服务节点之间的关系强度量化,从而为定量分析WSN模型中的社团结构提供一个更加精确的定义.

2.3 加权GN算法流程

在WSN中,社区之间所存在的连接往往是社区间通讯的瓶颈,是社区间通信时通信流量的必经之路.如果考虑网络中节点之间的通信并寻找到具有最高通信量的边,则该边就是连接不同社区的通道.若去掉这样的边,网络就可以自然分解成若干合理的社区.因此,加权GN算法的基本流程是不断地从网络中去掉加权边介数最大的边.加权GN算法的具体步骤如下:

① 计算网络中所有边的加权边介数;

② 找到加权边介数最大的边,将其从网络中移除;

③ 计算剩余边的加权边介数,重复步骤②;

④ 当网络中分裂出的每个社区都满足加权强社团的定义时,算法结束.

对于一个具有n个节点,m条边的网络来说,整个算法的复杂度为O(m2n)[8].移除一条边仅影响到与它属于同一个部分的那些边的加权边介数.因此,在反复计算时,只需重新计算与该边属于同一部分的那些边的加权边介数,而不必考虑其他的边.社团结构较强的网络往往很快就分裂成几个独立的部分,这样就大大减少了后续的计算量.对于尚未分解开的网络和已经分出一些社区的网络,算法的流程略有不同,算法流程分别如算法1和算法2所示.

算法1加权GN算法(初始网络)

输入:网络信息文件(包含节点和边的信息).

输出:网络的社团结构.

Begin

1 Initialize(); //初始化网络信息

2 CalculateEB(); //计算整个网络各边的加权边介数

3 DeleteEdge(); //删除加权边介数最大的边

4 if(IsDevide()) //判断是否产生新社团

5 InsertRear(NewCommunity); //新社团编号入队列

6 GetNewQ(); //计算模块度

7 if(Q<0)

8 break;

9 else

10 execute algorithm 2;//开始执行算法2

11 End if

12 else

13 goto 2; //继续寻找加权边介数最大的边

End

算法2加权GN算法(分解过程中网络)

输入:网络信息文件(包含节点和边的信息).

输出:网络的社团结构.

Begin

1 Initialize();

2 While(not TerminateCondition) //未满足终止条件时,

循环持续

3 if(TerminateCondition1) //判断网络是否完全退化

4 break;

5 if(TerminateCondition2) //判断是否所有社团均为加权强社团

6 break;

7 GetQueueFront(); //获取将要处理的社团(队首社团)

8 if(IsStrong()) //判断该社团是否为加权强社团

9 InsertRear();

10 if(IsSingle()) //判断该社团是否为单点社团

11 InsertRear();

12 CalculateEB(); //计算该社团各边的加权边介数

13 DeleteEdge();

14 if(IsDevide())

15 InsertRear(NewCommunity);

16 GetNewQ();

17 if(Q<0)

18 break;

19 End if

20 End while

End

当整个算法流程结束时,可能会出现以下3种情况:

1) 所有社团均为强社团结构;

2) 网络的模块度小于0;

3) 少量社团为单点社团.

情况1)是算法最理想的情况,此时挖掘出的网络社团结构即为本文要构建的Web服务社区.情况2)涉及到模块度Q的概念,模块度是Newman等[11]引进的衡量网络划分的标准.模块度越大,说明社团结构越明显.通常,模块度的局部峰值仅有1～2个.当模块度小于0时,如果继续分解网络,社团结构将变得更加不明显,因此在Q<0时立刻终止算法可得到相对良好的社团结构.情况3)涉及到单点社团,单点社团虽然不能再分,但它对构建Web服务社区不具备任何意义,事实上将其归并到其他社团会更加合理.对此,本文采取的做法是比较该单点社团所有连边的权值,将该节点加入到与其连边的权值最大的节点所在的社团中.

2.4 社区内服务相似度模型

为了验证构建出的社区结构的合理性,需制订一个相似度度量标准.为此,本文提出了一种基于语义相似关系的WSN社区内服务相似度模型.

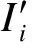
(8)

设网络中有M个社区V1,V2,…,VM,则整个网络的平均社区相似度定义为

(9)

本文在得到各个社区的服务相似度后,还将计算这些相似度的方差,以观察社区内服务相似度的稳定性,从而分析所构建的Web服务社区在网络中分布的合理性.

3 实验结果与分析

实验所用的测试数据来源于首届全国Web服务竞赛的数据集[12],数据集中Web服务输入输出的语义信息存储在WSDL文档和OWL文档中.本文采用DOM解析技术,从WSDL文档和OWL文档中将Web服务输入输出信息和相应的语义关系提取出来.然后将提取出的服务输入输出信息映射到概念层,分析任意2个服务之间的相似语义关系,建立节点之间的连接边.同时,计算2个服务之间的输入输出的相似度,作为边的权值存入数据库.

在完成数据的预处理工作后,为保证实验所得结论的准确性,以Web服务数据集中的服务作为节点,进行了多次实验. 分别以449,1 301和4 031个Web服务的服务集合作为实验对象,计算3个网络模型的聚类系数和平均最短路径长度,结果如表1所示.可看出,本文所构建的3个WSN模型具有较高的聚类系数和较小的平均最短路径长度,满足小世界特性.同时,3个WSN模型的度分布近似满足幂律分布的形态,说明它们具有无标度特性.

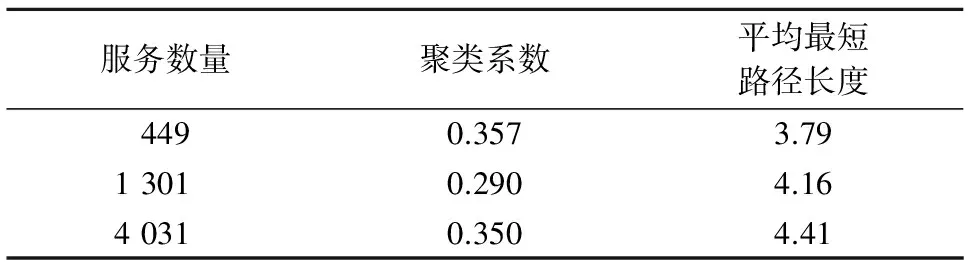
表1 网络模型属性值

本文分别采用Newman算法、自包含GN算法和提出的加权GN算法来构建Web服务社区.由实验结果可看出,Newman算法将网络分解为较多的细粒度社区,不能有效地完成Web服务社区的划分.自包含GN算法划分出的社区,规模极度不均衡,这种规模过大或过小的社区对实现Web服务社区的功能缺乏实际意义.在Internet中分布着各种不同功能的Web服务,不同种类的服务在数量上会有差异,但不应出现某一类服务的数量过度偏高的情况.本文提出的加权GN算法构建出的Web服务社区内服务数量较为均匀,符合实际情况.

为了验证所提算法的有效性,本文获得了3个不同规模的网络,使用3种算法分别进行服务的社区划分.针对每种算法获得的社区划分结果,使用社区内服务相似度模型计算社区内平均服务相似度以及相似度的波动情况,实验结果如表2所示.

表2 社区相似度比较

从表2可看出,本文算法构建出的Web服务社区的平均社区相似度更高.社区内的服务只有保持一定的相似度,才能使Web服务社区帮助完成服务分类和发现等工作.同时,本文算法构建出的Web服务社区,不同社区之间服务相似度的波动很小,相似程度趋于稳定,说明本文算法使不同类型的服务分布得更加合理.

4 结语

针对传统自包含GN算法应用于Web服务社区构建所存在的问题,本文提出了新的基于加权GN算法的Web服务社区构建方法.该方法克服了传统自包含GN算法仅考虑网络中节点连边情况的问题,在算法中加入了连边的权值信息,通过改进算法的删边条件和终止条件来完成Web服务社区的构建.实验结果表明,本文算法能够有效地在基于语义相似关系的WSN模型中完成Web服务社区的构建.与传统的自包含GN算法相比,本文算法提高了社区内服务的平均相似度,减小了网络中不同Web服务社区平均相似度的差别.由于本文实验采用的是首届全国Web服务竞赛的仿真数据集,和实际的Web服务环境可能会有所差异.以后的工作将着重研究如何为真实的Web服务库构建自身相应的语义体系,并在此基础上进行Web服务社区的构建.

)

[1] Popa V, Constantinescu L, Moise M, et al. Management of Web services communities, WSC system [J].StudiesinInformaticsandControl,2010,19(3):295-308.

[2] Chantal C, Vincent L, Jean-Francois S. Benefits of semantics on Web service composition from a complex network perspective [C]//ProceedingsofInternationalConferenceonNetworkedDigitalTechnologies. Berlin, Germany, 2010:80-90.

[3] Perryea C A. Community-based service discovery[C]//Proceedingsof2006IEEEInternationalConferenceonWebServices. Chicago, IL, USA, 2006:903-906.

[4] Zhang Xizhe, Yin Ying, Zhang Mingwei, et al. Web service community discovery based on spectrum clustering [C]//Proceedingsofthe2009InternationalConferenceonComputationalIntelligenceandSecurity. Beijing, China, 2009:187-191.

[5] Fortunato S. Community detection in graphs [J].PhysicsReports, 2010,486(3/4/5):75-174.

[6] 朱志良,邱媛源,李丹程,等. 一种Web服务复杂网络的构建方法[J]. 小型微型计算机系统,2012,33(2):199-205.

Zhu Zhiliang, Qiu Yuanyuan, Li Dancheng, et al. Approach for building complex network of Web service [J].JournalofChineseComputerSystems, 2012,33(2):199-205. (in Chinese)

[7] Fan Y, Li M H, Zhang P, et al. Accuracy and precision of methods for community identification in weighted networks [J].PhysicaA:StatisticalMechanicsanditsApplications, 2007,377(1): 363-372.

[8] 汪小帆,李翔,陈关荣. 复杂网络理论及其应用[M].北京:清华大学出版社,2006:164-169.

[9] Radicchi F, Castellano C, Cecconi F, et al. Defining and identifying communities in networks [J].ProcNatlAcadSci, 2004,101(9):2658-2663.

[10] 彭晖,史忠植,邱莉榕,等. 基于本体概念相似度的语义Web服务匹配算法[J]. 计算机工程,2008,34(15):51-53.

Peng Hui, Shi Zhongzhi, Qiu Lirong, et al. Matching algorithm of semantic Web service based on similarity of ontology concepts [J].ComputerEngineering, 2008,34(15):51-53.(in Chinese)

[11] Newman M E J, Girvan M. Finding and evaluating community structure in networks [J].PhysicalReviewE, 2004,69(2):026113-01-026113-15.

[12] China Web Service Cup (CWSC2011) [EB/OL]. (2011)[2012-10-15].http://debs.ict.ac.cn/cwsc2011/technical_details.html.