高速公路管理所综合成本选址模型

张卫华 缪子英 王 锟 丁 恒

(合肥工业大学交通运输工程学院,合肥 230009)

高速公路管理机构的规划和建设是实施高速公路有效管理的基础和前提,高速公路管理机构的选址问题越来越受到重视.我国高速公路管理一般采用管理处-管理所-收费站的管理模式,管理所是高速公路建设的重要组成部分,是高速公路的交通管理、养护、安全监控、收费、通信、服务设施等的直接业务管理部门,也是地区行政部门对高速公路实施管理的主要执行机构.

目前,国内外关于高速公路应急资源的配置与管理的相关研究较多,但对高速公路管理所选址布局问题的研究则较少[1-5].高速公路管理所布局选址建设往往缺乏理论方法支持.

本文以高速公路基本管理单位——管理所为研究对象,以全面性、适度性、均衡性为原则,从日常基本运营管理和事故应急救援2个方面进行管理所规划选址.高速公路管理所直接负责其管辖范围内高速公路的运营与管理,主要包括高速公路日常运营的基本运营管理和紧急情况下的交通事故应急救援,通过合理的高速公路管理所规划选址,可有效地提高高速公路运营效率,降低运营成本.当高速公路上发生交通事件时可及时进行救援,降低交通事件损失成本,从而使高速公路运营管理综合效益最大化.

1 高速公路路网构建及区域划分方法

以高速公路的交通路网作为建立高速公路管理所规划选址模型的研究基础.在交通网络分析中,每个交通路网节点均可以视为一个节点对象,将相邻两节点之间实际存在的交通路段设定为一条连接两节点的边.节点之间的可达性用阻抗表示,阻抗越大则可达性越低.将高速公路路网的数学集合定义为P(N,L,M),其中,N为节点集,L为弧段集,M为阻抗集.

建立的高速公路路网集合P(N,L,M)是一个较为复杂且庞大的交通网络,引入运筹学中的最小生成树[6],将交通网络P(N,L,M)划分为n个小交通网络Pi(Ni,Li,Mi),即Pi(Ni,Li,Mi)⊂P(N,L,M),其中Ni⊂N,Li⊂L,Mi⊂M,i=1,2,…,n.具体步骤如下.

① 在交通网络P(N,L,M)上任取一个闭环,去掉闭环中阻抗最大的边.当一个闭环上同时有2条以上阻抗最大的边时,则去掉其中任意1条,以保证节点的连通性.

② 重复步骤①,直到P(N,L,M)上无闭环存在为止.删除不连接边的孤独节点,余下的边和节点组成的生成树就是最小生成树.

③ 结合高速公路路网实际情况,将步骤②得到的最小生成树进行区域划分,划分原则为:各分区路段、节点及阻抗要尽量均匀;各分区大小要适中,达到一定要求的服务水平和救援时效;明确路段的分区归属问题,1个路段需全划入1个分区;分界处的节点要同时属于不同分区,保证每条路段至少有2个节点.

区域划分是一个不断反馈动态调整的过程.在模型优化及运算中,若不能满足要求则需重新进行区域的划分,以确定最优的区域划分,从而使模型优化求解结果满足要求,达到最优.

2 选址模型建立

本文将高速公路路网作为封闭的系统进行研究,分别从高速公路日常基本运营管理和交通事故应急救援2个方面,建立高速公路管理所选址模型,以综合成本最优为优化目标,确定最优的管理所选址.

2.1 日常基本运营管理成本选址模型

高速公路管理所对高速公路的日常基本运营管理是指不包含交通事故应急救援的基本工作,其基本职能主要是负责高速公路的养护、巡视、信息与监控等工作.高速公路管理所每天会以一定的频率发出车辆,保证高速公路上每隔一定的距离就有一辆管理所的车辆.同时,保证高速公路上的车辆能够均匀分布、循环管理,从管理所出发沿最佳路径再回到管理所.基于高速公路日常基本运营管理的选址模型,是在寻找从管理所出发再回到管理所的双向遍历最短路径的基础上建立的.

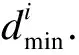
ZRC=Zn+Zf+Zo=

(1)

式中

2.2 交通事故应急救援成本选址模型

交通事故发生后,应急救援设施能够在有效的时间内及时到达事故点进行救援,是应急救援的关键.本文根据交通事故的空间分布特征[7]及潜在交通事故分析方法[8],结合新建高速公路的道路线形、道路横断面、路面类型、路面状况等设计指标,分析得到高速公路的潜在交通事故隐患点分布情况.以高速公路路网中的潜在交通事故隐患点为管理所选址影响因素,建立交通事故应急救援成本选址模型.

由于到达事故点的时间不同,产生的救援效果也不相同.将权值为1的事故发生至应急救援资源到达现场的时间称为交通事故应急救援滞后时间t,将不同救援效果对应下的人员伤亡和财产损失等称作救援效果损失成本f(t).随着救援时间的增加,救援效果逐渐下降,救援效果损失成本逐渐增大,当时间到达一定值,救援效果损失成本将趋于定值.

交通事故应急救援滞后时间t与交通事故应急救援效果损失成本f(t)之间的关系见图1.交通事故一旦发生,无论救援设施以多么少的时间达到事故点,交通事故都会造成一定的基本损失,这部分的基本损失成本与救援滞后时间t无关,将这种基本损失成本记为Zb.随着救援滞后时间t的增加,交通事故造成的人员、财产损失将增加.在不考虑交通事故造成的交通延误损失下,当救援滞后时间t超过救援时效t0时,交通事故造成的损失将趋于定值Zm,基本不再随着应急救援滞后时间t的增加而改变.

图1 t-f(t)曲线图

(2)

(3)

因此,高速公路交通事故应急救援产生的总成本为

(5)

2.3 综合成本选址模型

综合考虑高速公路日常运营管理成本及交通事故应急救援成本2个方面,以综合成本最小为目标,建立高速公路管理所选址模型.

高速公路管理综合成本为

(6)

目标函数及约束条件为

Z*=minZ

(7)

3 模型求解

3.1 最短路径求解

3.1.1 双向遍历最短路径

由于高速公路是中央分隔双向行驶的,在对高速公路进行日常运营管理时需要在高速公路上进行2次方向相反的行驶.行驶的最优路径应满足车辆从管理所出发,在高速公路各路段上进行至少1次方向相反的行驶,行驶完其负责的所有路段后回到管理所.将按照这种规则访问所有路段的过程称为高速公路路段双向遍历.运用有向图上的投递员问题解法[10],便可求得从管理所出发再回到管理所的双向遍历最优路径.

3.1.2 管理所至节点及事故隐患点最短路径

3.2 综合成本选址模型计算流程

按照一定的服务水平要求进行高速公路区域划分,然后进行各个分区管理所初始选址,对各个分区管理所选址初始方案运用无约束最优化方法中的最速下降法[13]进行算法迭代优化.由于各个分区的路网节点和边是有限的,管理所选址是一个无约束、收敛问题,因此可以运用最速下降法进行计算求解.

高速公路管理所选址流程图见图2.

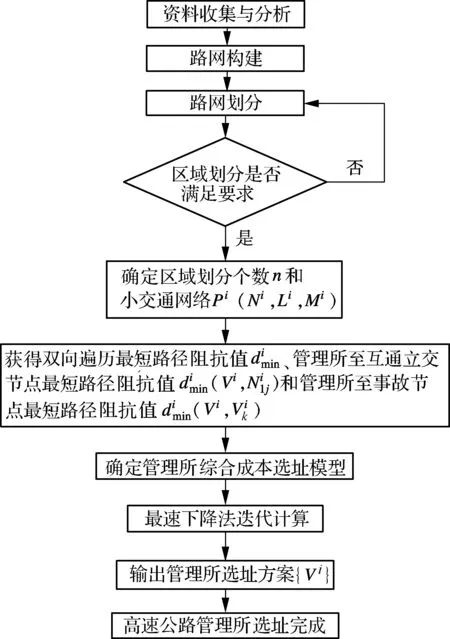
图2 高速公路管理所选址流程图

4 应用实例分析

下面以某地区规划高速公路路网为例,进行实例应用分析.

4.1 路网构建

图3 高速公路网络图

分析交通事故分布特征和规划高速公路道路线形、道路横断面、路面类型、路面状况等设计指标,预测潜在交通事故隐患点集合为{(Q1,A,B,20),(Q2,E,F,25),(Q3,F,J,16),(Q4,G,K,16),(Q5,D,H,31)},交通事故隐患点对应事故级别分别为Ⅰ,Ⅱ,Ⅱ,Ⅲ,Ⅳ级.

4.2 计算结果分析

本文模型中的参数需要根据大量的调查数据进行标定.假设参数已知,并用距离表征阻抗.高速公路进行日常基本运营管理时,每次发车的资源数量γ=1 套/次,单套信息与监控设备成本β=1.0×107元/套,单位阻抗所需的成本α=1.0×102元/(套·km),单位服务半径损失成本δ=1.0×104元/km,救援效果损失成本f(t)与救援时间t的关系为

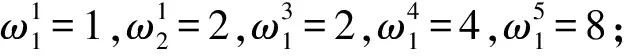
取初始方案为

初始方案对应下的综合成本Z0=54 078 513元;服务半径分别为82,67,80,110,52 km;救援时间分别为9.5,28.5,8.5,7.5,14.5 min,有一处超过救援时效.

以初始方案为基础,进行优化求解,得到最优管理所选址位置为

{Vi|i=1,2, …,5}={(V1,A,E,20),(V2,B,

C,19),(V3,F,J,24),(V4,J,K,

26),(V5,D,H,55)}

5 结语

本文综合考虑高速公路日常运营管理成本和事故救援成本,以救援时效为约束条件,以综合成本最优为目标,引入路网复杂性和潜在交通事故隐患点等影响因素,通过量化高速公路选址因素建立模型,对高速公路高效运营下的管理所选址具有重要的理论依据和实际应用.实例应用表明,在降低了综合成本的同时得到了分布均衡的最优管理所选址位置.此外,模型建立过程中的参数标定需要大量数据,或通过复杂的公式进行数学推导求得近似值.本文实例应用的参数标定较为简单,模型参数的标定有待进一步研究.通过精度设置及优化运算程序,可以使近似最优方案以最小的误差接近严格意义上的真正最优方案.

)

[1] 吕宗让.高速公路沿线建筑设施设计[J].黑龙江交通科技,2008(9):21.

Lü Zongrang. Construction design along the expressway[J].CommunicationsScienceandTechnologyHeilongjiang, 2008(9): 21.(in Chinese)

[2] 柴干,杨晓光.高速公路紧急救援系统的体系框架与实施方案研究[J].交通与计算机,2007,25(4):78-81.

Chai Gan, Yang Xiaoguang. Architecture and implementation scheme of expressway emergency rescue system[J].ComputerandCommunications, 2007,25(4): 78-81. (in Chinese)

[3] 王菲.高速公路交通事故紧急救援时间模型及救援站点布局研究[D].重庆:重庆交通大学交通运输学院,2008.

[4] 方磊.基于偏好DEA模型的应急资源优化配置[J].系统工程理论与实践,2008,28(5):98-104.

Fang Lei. Emergency resource optimizing configuration based on DEA model[J].SystemsEngineering—Theory&Practice, 2008,28(5): 98-104. (in Chinese)

[5] Fu Deqiang, Tang Xiaoming. Research on location model of emergency logistics based on AHP/DEA [C]//IEEEInformationManagement,InnovationManagementandIndustrialEngineering. Shenzhen, China, 2011: 472-474.

[6] Boria N, Paschos V T. Fast reoptimization for the minimum spanning tree problem [J].JournalofDiscreteAlgorithms, 2010,8(3): 296-310.

[7] 过秀成,盛玉刚.公路交通事故黑点分析技术[M].南京:东南大学出版社,2009:1-6.

[8] Chen Yan, Wu Hangbin, Liu Chun, et al. Identification of black spot on traffic accidents and its spatial association analysis based on geographic information system [C]//Proceedingsof2011IEEENaturalComputation. Shanghai, China, 2011: 143-150.

[9] 程振华.高速公路交通事故紧急救援管理研究[D].成都:西南交通大学交通运输学院,2006.

[10] Prakash S, Sharma M K, Singh A. A heuristic for multi-objective Chinese postman problem [C]//Proceedingsof2009IEEEComputers&IndustrialEngineering. Troyes, France, 2009: 596-599.

[11] Nian Lai, Zheng Jinhua. Hybrid genetic algorithm for TSP[C]//Proceedingsof2011IEEEComputationalIntelligenceandSecurity. Sanya, China, 2011: 71-75.

[12] Fan Yuezhen, Wang Qingchun, Lu Dunmin, et al. An improved Dijkstra algorithm used on vehicle optimization route planning [C]//Proceedingsof2010IEEEComputerEngineeringandTechnology. Chengdu, China, 2010: 693-696.