具有负载平衡动态路由选择的排队网络的稳定性研究

唐柏荣， 王知人， 涂建新， 李泉林

(1.燕山大学计算数学系 河北秦皇岛066004;2.燕山大学管理科学与工程系 河北秦皇岛066004)

，即增广流体模型弱不稳定．必要性证

0 引言

排队网络服务顾客的效率高低与排队网络是否稳定密切相关，而排队网络收益与排队网络服务顾客的效率也是密切相关的，因此排队网络的稳定性问题倍受关注．许多学者对具有多个顾客类的排队网络的稳定性问题进行了研究，如文献［1-2］得出了具有多个顾客类的排队网络稳定的充分条件，其主要条件是排队网络相应的流体模型稳定．一些学者对每个服务站具有单服务台的排队网络的稳定性问题进行了研究，如文献［3］中每个到达者随机选取两个服务台，然后加入较短的队列，得到了队长的渐近分布存在的充分条件．文献［4］得到队长过程正常返的充分条件．文献［5］中到达间隔时间和服务时间都服从一般分布，当J=2时通过流体模型得到了一个排队网络稳定的充要条件以及一个排队网络不稳定的充分条件．一些学者对每个服务站具有多服务台的排队网络的稳定性问题进行了研究，如文献［6］研究了具有J个服务站且每个服务站都具有N个服务台的排队网络，到达间隔时间和服务时间都服从指数分布，一个突出的特点是出现了检验数分布的概念．每个到达者和每个接受完服务但仍留在网络的顾客都要加入到一个服务台集(样本)中的某个最短队列，得到了q过程和r过程正常返的充分条件和必要条件．与文献［6］中模型不同的是，文献［7］的模型中每个到达者选取的样本所包含的服务台数不变;而文献［8-9］的模型中外部到达过程与服务站相关，而不是与检验数分布相关，通过流体模型得到在一些假设下流体逼近存在．文献［10］研究的是具有K个更新到达流和N个服务台的JSQ(进入最短队列)网络，每个到达者进入选择集(服务台集)中具有最短队列的服务台前排队，而且每个顾客的服务时间服从一般分布，而本文中每个到达者在哪个服务台前排队是与检验数分布有关的，并且到达流都是泊松到达流，每个顾客的服务时间服从指数分布．综上所述，对于具有负载平衡动态路由选择的网络的稳定性研究尚不多见．

鉴于此，作者在文献［5-6］的研究基础上，对每个服务站具有多服务台、出现了检验数分布的概念、每个到达者和每个接受完服务但仍留在网络的顾客都要加入到一个服务台集(样本)中的某个最短队列，即利用概率知识对具有负载平衡动态路由选择的排队网络的稳定性问题进行了随机分析，所用的方法与文献［11］类似．

1 预备知识

首先介绍负载平衡模型并给出模型的假设．

定义1 对于任意的θ∈Θ，存在一个相应的具有到达时间序列{ξθ(n):n≥1}的外部到达过程，被称为θ型外部到达过程．

假设每个服务台都是非闲置的和每个服务台的服务规则都是先进先出．由于θ型外部到达过程，第1个顾客到达的时刻为 ξθ(1);第 n － 1、n个顾客的到达时间间隔为 ξθ(n)，n≥2．ηi，k(n)，n≥1 表示被服务台(i，k)服务的第n个顾客的服务时间．假设对任意的θ∈Θ都有{ξθ(n):n≥1}独立且同分布;对任意的(i，k)∈C都有{ηi，k(n):n≥1}独立同分布;所有到达间隔时间序列和所有服务时间序列都相互独立．若A为集合，则表示A中元素的个数;若y为向量，则表示y的1范数．JSQ表示加入最短队列，并且排队网络简称为网络．

以下介绍网络状态和网络过程．

用 X(t)=(Z(t)，U(t)，V(t))表示网络在 t时刻的状态，其中，Z(t)={Zi，k(t):(i，k)∈ C}，U(t)={Uθ(t):θ∈ Θ}，V(t)={Vi，k(t):(i，k)∈ C}．Zi，k(t)表示 t时刻服务台(i，k)的队长;Uθ(t)表示 t时刻 θ型外部到达过程的剩余到达间隔时间;Vi，k(t)表示(i，k)服务台中正在服务的顾客在t时刻的剩余服务时间，则状态空间S为R2NJ+|Θ|的子集．假设网络过程X={X(t):t≥0}右连续且具有左极限，则由文献［1］的命题2．1可知，X是强马尔可夫过程．

2 流体模型

先给出描述JSQ网络动态行为的关系式组．

用 Ai，k(t)表示［0，t］中外部和内部到达服务站 i中并要被服务台(i，k)服务的顾客数;Eθ(t)表示［0，t］中由于θ型外部到达过程而从网络外部到达的顾客数;Di(t)表示［0，t］中服务站i上接受完服务的顾客数;Ti，k(t)，Ii，k(t)分别表示［0，t］中服务台(i，k)的工作时间积累和空闲时间积累;Si，k(t)表示服务台(i，k)花费t单位时间服务完的顾客数;Φi，θ(n)表示从服务站i上离去的前n个顾客获得检验数分布θ的个数．当(i，k)∈C及t≥0时，描述JSQ网络的动态如下:

因为Si，k(Ti，k(t))表示在［0，t］中服务台(i，k)服务完的顾客数，Ai，k(t)表示［0，t］中外部和内部到达服务站i中并要被服务台(i，k)服务的顾客数，所以有

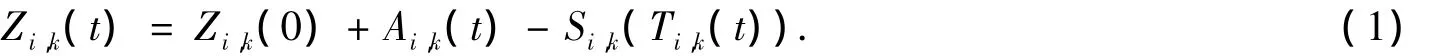
因为t时刻服务台(i，k)的队长至少为空，所以有

因为 Ti，k(t)，Ii，k(t)分别表示［0，t］内服务台(i，k)的工作时间积累和空闲时间积累，所以有

因为服务台(i，k)都是非闲置的，所以有

如果对任意的 u∈ (s，t)都有 Zi，k(u)＞ 0，则

因为Si，k(Ti，k(t))表示在「0，t■内服务台(i，k)服务完的顾客数，Di(t)表示［0，t］内服务站i上接受完服务的顾客数，所以有

如果 Μ ⊆J，0≤s≤t且对任意的k，l=1，2，…，N，i∈ Μ，j∈J－ Μ，及u∈(s，t)都有Zi，k(u)＞Zj，l(u)，则有

式(7)和(8)执行了顾客的JSQ路由选择行为．

下面介绍流体极限的概念，先给出一个引理．

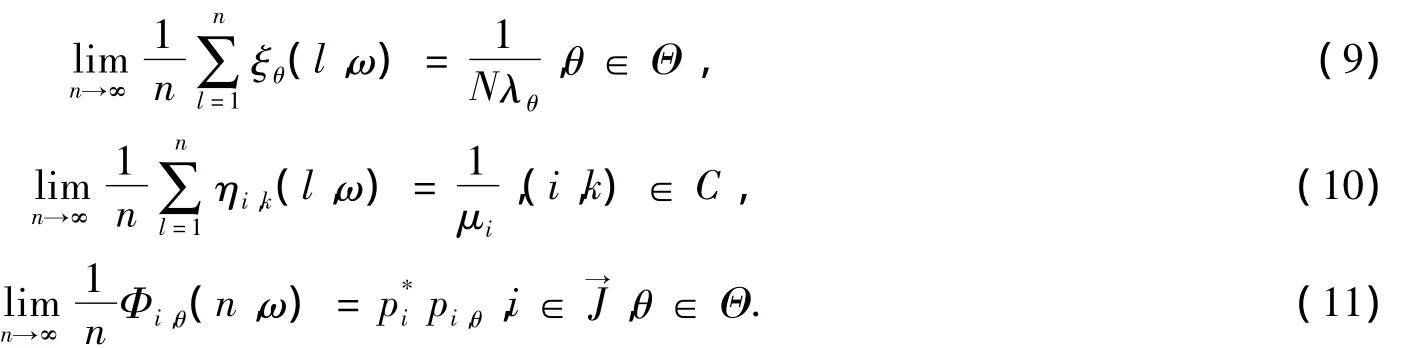
证明 因为{ξθ(n)，n≥1}，θ∈Θ是独立同分布随机变量序列

由文献［1］的定理4．1，给出了流体极限的定义．

定义2 对任意一个满足(9)～(11)的ω及任意一个使得{xr/r:r＞0}有界的初始状态集{xr:r＞0}，必存在一个子序列rn→∞ 使得在［0，∞)的任意一个紧集上都一致收敛到=(·)，(·)，(·)，(·))，则称为流体极限．

因为a．s．是几乎必然的意思，所以(9)成立;同理，(10)成立．

其中，xr=(zr，ur，vr)，则称为无延迟的流体极限．

根据文献［12］知，如果利用流体极限来研究网络的稳定性问题，则只需考虑无延迟的流体极限．

为了获得流体模型关系式组，先给出引理2．

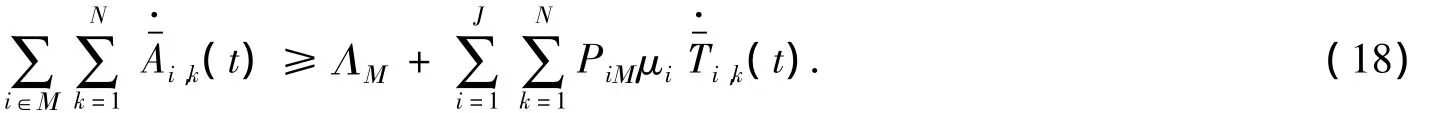
式(13)～(19)为流体模型关系式组，其解称为流体模型的解．都 Lipschitz连续以及(13)～ (19)成立即可，在文献［2］中可以找到另外两个要证的结论．设ω满足(9)～(11)，则可以选取xr的子序列xrn使得对某个(·)，在非负有理数集上恒有

证明 只需证明

同理可得

在先进先出规则下，用 Γi，k(n)表示服务台(i，k)服务完的前 n个顾客的服务时间之和，则恒有Γi，k(Si，k(Ti，k(t)))≤ Ti，k(t) ＜ Γi，k(Si，k(Ti，k(t))+1)，即

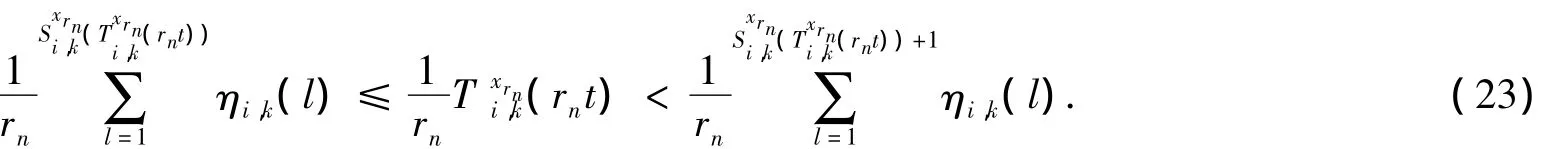
由(10)可知，对任意给定的ε＞0以及足够大的n，(23)的最右边项都小于等于

而对任意给定的ε＞0以及足够大的n，(23)的最左边项都大于等于

取n→∞，夹逼得

由(11)、(24)可知，当n→∞ 时，

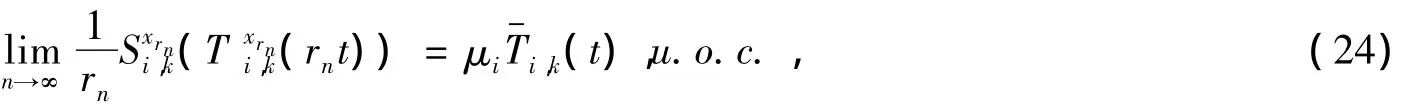
与上一段的证明类似，由(9)可知

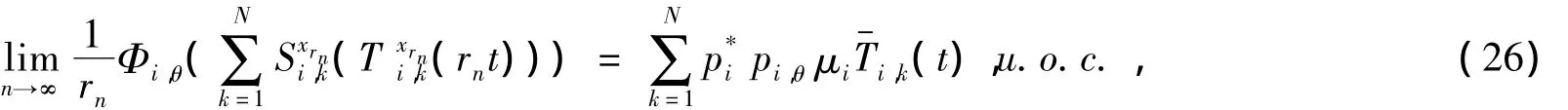
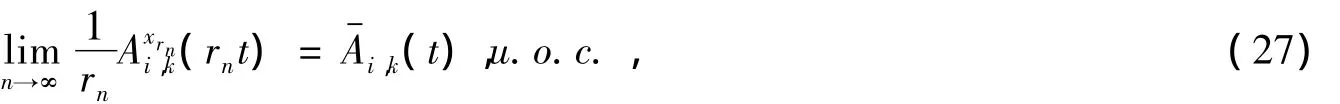
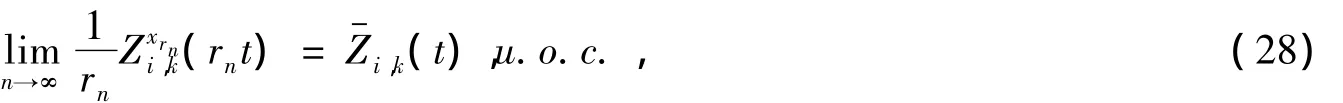
所以当(7)、(8)中 s→ t时，(18)、(19)成立．又因为(·)Lipschitz连续，所以(·)也 Lipschitz连续．如果选取一个子序列 rn使得(0)存在，由(1)、(24)和(27)可知因为(·)和(·)都Lipschitz连续，所以(·)也Lipschitz连续．由(1)、(2)、(24)、(27)以及(28)可知，(13)、(14)成立．当(5)中 s→ t时，由(22)、(28)可知，(17)成立．引理2证毕．

下面给出流体模型稳定和弱不稳定的定义，为了将网络和其相应的流体模型联系起来，给出了引理3和引理4．

引理3［1］如果流体模型稳定，则马尔可夫过程是Harris正常返的．

引理4［14］如果流体模型弱不稳定，则马尔可夫过程不稳定，即对每个固定的初始状态x，当t→∞时都以概率1收敛到无穷．

3 增广流体模型

其中，Ρx－a．s．表示初始状态为x时以概率1收敛．所以对每个具有固定的初始状态的流体极限，都有

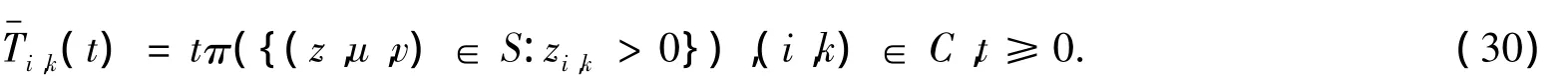
现选择一个紧集K⊆S，使得 π(K)=∫SΡ(z，u，v)(X(t)∈ K)dπ(z，u，v)＞ 0，t≥0．因为对任意的 x ＞ 0，都有 Ρ(ξθ(1)≥ x)=1 － Ρ，所以存在一个 t0＞ 0，使得对任意的(z，u，v)∈ K 都有 Ρ(z，u，．因此有

故由(30)得到(29)．引理5证毕．

式(13)～(19)及式(29)为增广流体模型关系式组，其解称为增广流体模型的解．

引理6对证明马氏过程不是Harris正常返非常有用，因为只需要证明增广流体模型弱不稳定即可．

4 主要结果

文献［5］研究的是单服务台情形，而作者研究的是至少具有两个服务站、每个服务站至少具有两个服务台的情形;文献［6］中服务强度恒为1，而作者研究的是服务强度与服务站有关，即文中的模型较文献［5－6］复杂，所以通过假设1使得模型稍微简单一些．

假设1 对任意一个 θ∈Θ，p*i，pi，θ都与i无关．对于 Μ⊆，令PΜ=PiΜ，假设p*＜1，p*=p*i，pθ=p，λ*= Λ ．i，θJ

证明 因为属于同一服务站的服务台对称，所以Μ满足(19)．由(19)有

将(32)减去(33)得

由(34)和(35)得

将(36)、(37)代入(33)得

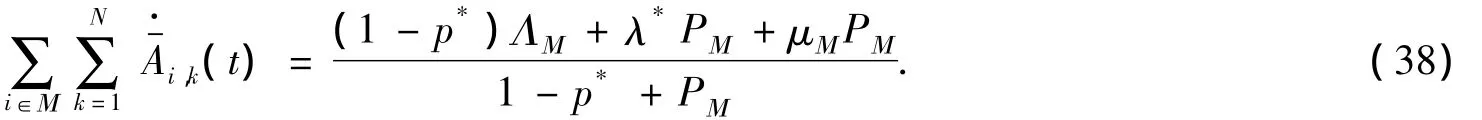
由(13)、(37)有

将(38)代入(39)即可得到(31)．引理7证毕．

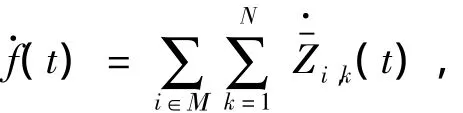
由引理7，对任意这样的t，有

由(41)可知流体模型稳定．由引理3可知充分性证毕．

再证必要性．根据引理6，只需证明如果(40)不成立，增广流体模型则弱不稳定．设存在Μ⊆J→使(40)不成立．设为一个具有(0)=0特点的增广流体模型的解．

由(13)、(18)得

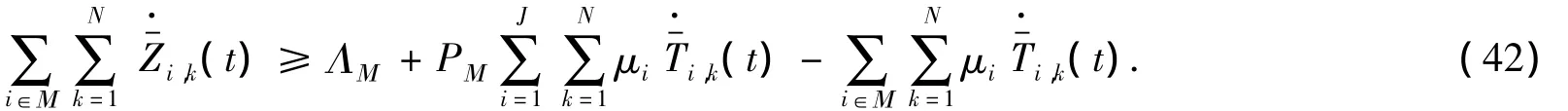
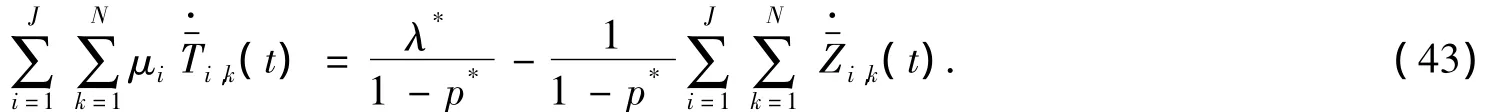
将(43)代入(42)，得

由(29)得

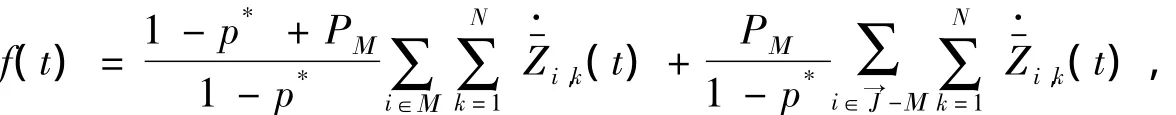
因为Μ使(40)不成立以及(44)，所以对所有的t≥0，都有

令毕．所以定理1证毕．

，即增广流体模型弱不稳定．必要性证

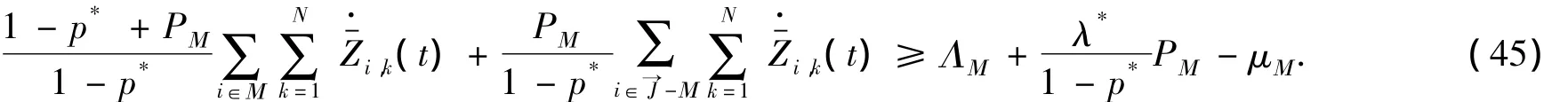
证明 由(13)、(18)得

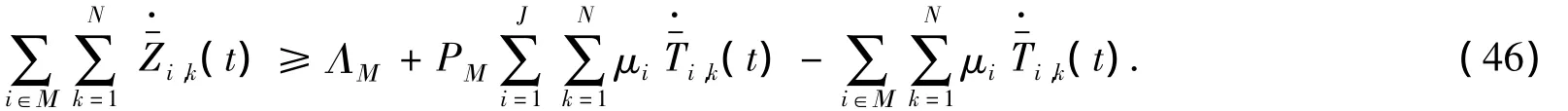
在(19)中取 Μ =J，由(13)、(19)得

将(47)代入(46)，得

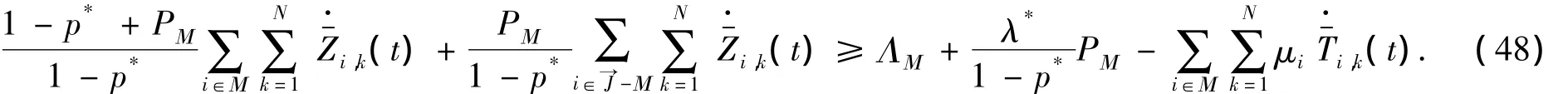
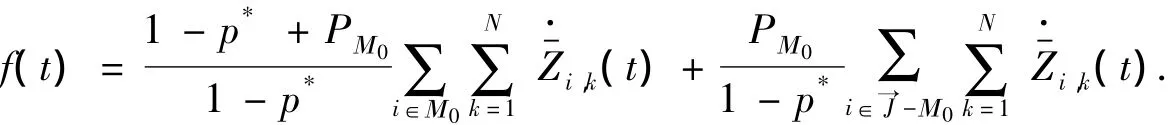
由引理8可知，对所有的t＞0有·f (t)＞ 0．从而f(t)＞ 0，因此对所有的t＞ 0，有 Z－(t) ＞0．故流体模型弱不稳定，由引理4可知定理2得证．

［1］ Dai Jiangang.On the positive Harris recurrence of multiclass queueing networks:a unified approach via fluid limit models［J］.The Annals of Applied Probability，1995，5(1):49-77.

［2］ Maury B.Stability of Queueing Networks［M］.Berlin:Springer，2008:81-131.

［3］ Vvedenskaya N D，Dobrushin R L.Queueing system with the shortest of two queues:an asymptotic approach［J］.Problems of Information Transmission，1996，32(1):15-29.

［4］ Foley R D，Mcdonald D R.Join the shortest queue:stability and exact asymptotics［J］.The Annals of Applied Probability，2001，11(3):569-607.

［5］ Dai Jiangang，Hasenbein J J，Kim B.Stability of join-the-shortest-queue networks［J］.Queueing Systems，2007，57(4):129-145.

［6］ Suhov Y M，Vvedenskaya N D.Fast Jackson networks with dynamic routing［J］.Problems of Information Transmission，2002，38(2):136-153.

［7］ Martin J B，Suhov Y M.Fast Jackson networks［J］.The Annals of Applied Probability，1999，9(3):854-870.

［8］ 郭永江.每个节点具有多服务台的Jackson网络流体逼近的收敛速度［J］.系统科学与数学，2008，28(9):1118-1133.

［9］ Chen Hong.Fluid limits and diffusion approximations for networks of multi-server queue in heavy traffic［J］.Discrete Event Dymamic Systems，1994，4(3):269-291.

［10］ Bramson M.Stability of join the shortest queue networks［J］.The Annals of Applied Probability，2011，21(4):1568-1625.

［11］赵湘育，王东炜，张刚.网络系统可靠度和单元概率重要度的随机模拟分析［J］.郑州大学学报:理学版，2009，41(4):108-111.

［12］ Bramson M.Stability of two families of queueing networks and a discussion of fluid limits［J］.Queueing Systems，1998，28(1/2/3):7-31.

［13］徐丽.函数列一致连续和一致收敛及等度连续的关系［J］.上海电力学院学报，2007，23(3):284-287.

［14］ Dai Jiangang.A fluid-limit model criterion for instability of multiclass queueing networks［J］.The Annals of Applied Probability，1996，6(3):751-757.