竖式法在地理计算中的运用

广东省惠州市惠阳中山中学（ 516211） 熊国权

对于竖式我们并不陌生，早在小学算术运算中我们就接触到大量的加、减、乘、除等竖式运算，作为一种运算工具，其好处人人皆知。在高中地理教学中，涉及四个相关变量之间的换算，一般也可以运用竖式法进行计算。

一、竖式法在正午太阳高度计算中的运用

对于正午太阳高度的计算，目前常用的方法有公式法和图解法。其中，公式法如下：

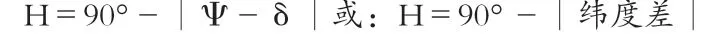
（其中：H为所求地正午太阳高度，Ψ为当地地理纬度，永远取正值，δ为太阳直射点的纬度，当地夏半年取正值，冬半年取负值。）

图解法如下（图1）：

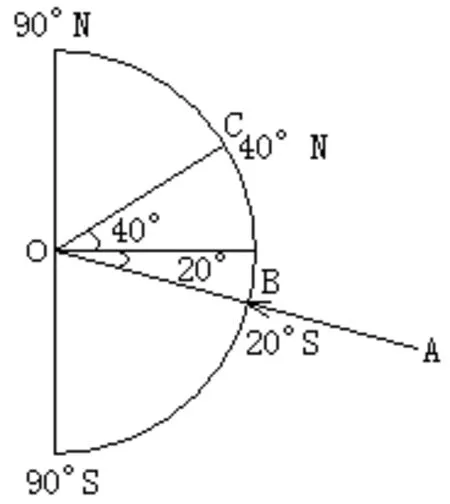
图1

当太阳直射点位于B时，求C点的正午太阳高度：H＝90°－（20°＋40°）。

上述两种方法在实际运用过程中都存在一定程度的缺陷：其一，公式法虽然实现了计算原理的数学表达，科学性、严谨性自不必说，但是直观性不强，容易导致机械记忆，随之产生的问题是容易遗忘，并且每个字母代表什么容易产生混淆。其二，图解法虽然直观，原理一看便懂，但画图过程比较繁琐，还不够“轻便”。

为此，笔者设计竖式法予以改进，基本方法如下：

如图2，X1和X2分别表示所求地的纬度和太阳直射点的纬度，H1和H2分别表示X1和X2两地的正午太阳高度，要想求出第四个变量，必需知道其它三个变量，然后根据正午太阳高度差等于纬度差，即△H＝△X，求出第四个变量。

图2

例如，北半球冬至日，北纬40度的正午太阳高度是多少？运用竖式法计算如下（图3）：

图3

从上面的例子可以看出，与公式法和图解法相比，竖式法至少有以下几个优点：第一，可以清楚和直观地表明变量和变量之间的关系，使运算过程简单、明了；第二，在运算过程中内部表征和外部表征相结合，避免过多地占用工作记忆空间，释放了脑力资源。第三，形式抽象和简约，实现了工具的“小巧化”，使用起来十分“轻便”和快捷。

使用竖式法计算正午太阳高度应注意的问题主要有：第一，必须明确“正午太阳高度从直射点向南北两侧递减，直射点南北两侧对称”（“同侧递减，异侧对称”）的基本原理；第二，如果两地不在同一侧时，应根据对称性将其转化为同一侧进行计算。第三，纬度差的计算应遵循“同侧相减，异侧相加”的原则，例如北纬20度与南纬20度之间的纬度差是40度而不是0度。

二、竖式法在地方时计算中的运用

竖式法也常常用于地方时的计算，基本方法如图4所示，X1和X2分别表示两条经线的经度，T1和T2分别表示X1和X2的地方时，如果知道了其中的三个变量，就可以根据“经度每15度相差1小时”或“经度每1度相差4分钟”，求出第四个变量。在计算时间的时候，应注意遵循“东早西晚，东加西减”的原则，在计算经度差的时候应遵循“同侧相减，异侧相加”的原则。

图4

例如，当东经150度的地方时是2013年3月1日6时整，西经150度的地方时是多少？运用竖式法计算如下（图5）：

图5

三、竖式法在区时计算中的运用

竖式法同样也可以运用于区时的计算，只需要将两条经线换成两个时区即可。如图6，X1和X2分别表示两个不同的时区，T1和T2分别表示X1和X2的区时，知道了其中的三个变量，就可以根据“时区（数）差＝区时差”、“东早西晚”、“东加西减”等规则求出第四个变量。

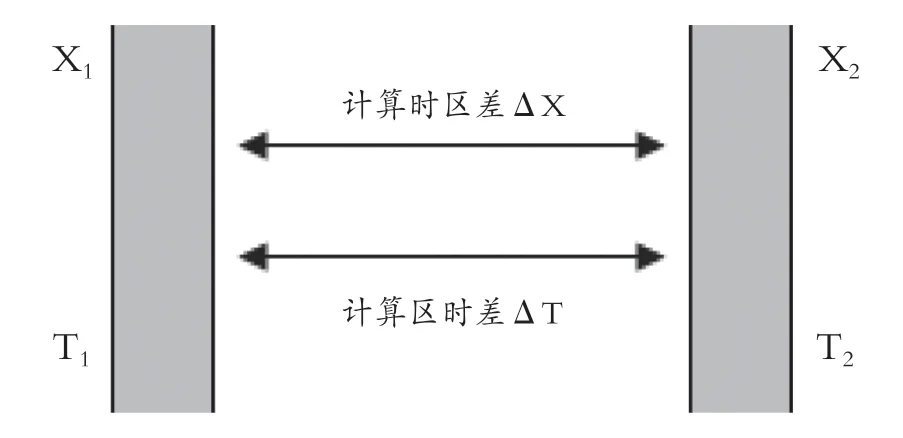
图6

例如，央视网消息：国家主席习近平于当地时间2013年03月22 日11时55分抵达莫斯科，开始对俄罗斯进行国事访问。请问：当习近平抵达莫斯科时，北京时间是几点钟？（莫斯科位于东三区）运用竖式法计算如下（图7）：

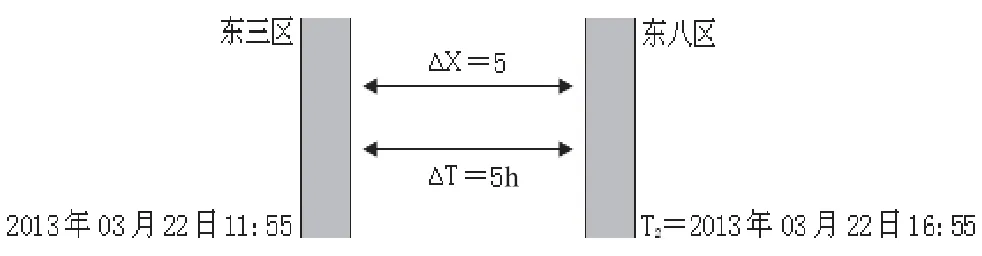
图7

四、竖式法在海拔和气温计算中的运用

竖式法还可运用于海拔高度与气温变化之间的换算。例如，如图8，已知该山脉顶部有永久性积雪，测得P点的年平均气温大约是12℃。求该山脉雪线的海拔高度大约是多少？

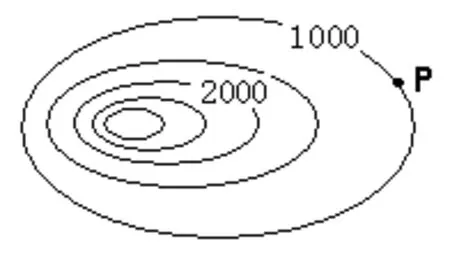
图8

对于这样的题目，运用竖式法计算比较简便。如图9，h1和h2分别表示两地的海拔高度，t1和t2分别表示h1和h2两地的气温，如果知道p点的海拔和气温以及雪线处的气温，就可以根据“海拔每升高100米，气温下降0.6℃”求出雪线的海拔高度。

图9

将数值代入上面的竖式，就可以求得雪线的海拔高度大约为3000米（如图10）。

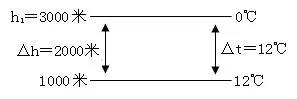
图10