基于LabVIEW语言的地铁列车能量互馈型交流传动仿真平台设计＊

2013-03-17 00:52吕建国胡文斌李培伟王勇博吴超飞

城市轨道交通研究 2013年12期

关键词：传动转矩偏差

吕建国胡文斌李培伟王勇博吴超飞

（1.南京理工大学能源与动力工程学院，210094，南京；2.南京理工大学自动化学院，210094，南京∥第一作者，博士研究生）

为了对地铁列车站间的牵引过程进行离线模拟，本文基于LabVIEW语言对“双逆变器双电机”能量互馈型交流传动仿真平台进行研究。该仿真平台运用了目前国际上较为先进的交流传动仿真试验方法。

本文介绍的仿真试验平台通过LabVIEW语言对电机进行矢量控制，通过LabVIEW设计的界面按照实际的地铁站间运行数据控制牵引电机和负载电机的转速与转矩，测量母线侧的电流数据，分析列车牵引系统的节能特性，为进一步研究列车牵引策略打下基础。

1 能量互馈型牵引系统的工作原理

“双逆变器-双电机”能量互馈型牵引系统由一个四象限变流器和两个共直流母线的逆变器构成，如图1所示。四象限变流器整流出的直流电供给逆变器INV1和INV2。INV1控制牵引电机M1的定子频率大于转子频率，运行于电动状态，其电磁转矩与电机旋转方向相同，提供互馈试验台的牵引力。M1通过联轴器带动负载电机M2转子同步旋转，实现能量的有效传导。INV2控制M2的定子频率小于转子频率，运行于发电状态。M2的力矩作为M1的模拟负载阻力矩，由上位机控制INV2调节负载阻力矩，使之运行于特定的负载曲线，达到模拟各种工况的目的。同时，INV2将M2发出的交流电能回馈至母线侧，供给M1使用，或者通过变流器回馈电网，使能量得到充分利用。

2 仿真试验平台主要结构

仿真试验平台的主要结构如图2所示。

图1 双逆变器双电机能量互馈型牵引系统结构

图2 仿真试验平台的硬件结构

电网电能经过LCL（电感-电容电感）滤波器后进入试验系统。滤波电路的结构如图3所示。其中，滤波器输出端的扼流圈和电容用于滤除信号中的高频分量；电网侧与地相连的电容以及两端跨接的电阻用于当输入功率断开时对电容器进行放电处理，试验中设置的放电电阻规格为10mΩ、0.5W。

图3 LCL滤波电路

滤波器输出端连接四象限变流单元，仿真试验平台中使用主动前端（Active Front End，简为AFE）完成四象限变流器功能。AFE无论在整流还是逆变状态下均通过IGBT（绝缘栅双极型晶体管）开关状态的切换来实现相应的功能。因此，两种状态下网侧的电流都是谐波很少的正弦波，功率因数也接近于1，大大减少了对电网的干扰［3］。AFE的拓扑为一个Boost逆变器，因此在AFE后侧的母线电压会高于电网电压峰值，可以在电网电压较低时或波动较大时保持直流母线电压的稳定［4］。

直流母线前端挂接AFE变流单元，后端挂接两套相同的逆变装置，分别控制两台异步电机。两电机轴端接有转矩传感器。该传感器可以测量轴端的机械转速和转矩信号，传感器的输出信号均为等幅值脉冲，幅值大小为8V。转矩和转速大小与输出脉冲频率的关系为：

式中：

T——输出转矩，Nm；

fT——转矩输出脉冲频率，kHz；

fn——转速输出脉冲频率，kHz；

n——输出机械转速，r／min；

Z——传感器测速齿数，此处Z取60。

由传感器采样到的脉冲信号经过积分器转换为电压信号，转换关系为：

式中：

uT——转矩电压信号；

un——转速电压信号。

电机转矩和转速的电压信号范围分别为－5V～5V和0～5V。为避免功率电路对弱电控制单元的噪声影响，由传感器得到的弱电信号需要经过线性光耦隔离芯片进行隔离与整形。隔离后的信号送入NI（美国国家仪器有限公司）数据采集板卡。由转矩传感器得到的信号作为反馈信号送入上位机进行处理；上位机使用基于电压偏差解耦的转子磁场定向矢量控制策略对电机进行控制。

3 偏差解耦矢量控制

在保证仿真试验平台2台电机中1台处于牵引电动状态、1台处于负载发电状态的基础上，为了实现对仿真试验平台任意状态的精准控制，需要分别对牵引电机实行转速闭环，对负载电机实行转矩闭环，并应用矢量控制算法。

3.1 感应电动机数学模型

当按转子磁链定向时，感应电动机电压方程［5］如下：

式中：

Rs——定子电阻；

isd——定子励磁电流分量；

isq——转矩电流分量；

Ls——定子自感；

Lr——转子自感；

Lm——定转子间的互感；

ω1——旋转磁场同步转速；

Ψr——转子磁链。

对应式（5）、（6）的电动机动态结构图［6］如图4所示。从图4可以看到：动态结构图中存在着定子励磁电流分量isd和转矩电流分量isq的交叉耦合，使得转矩电流的调节受到励磁电流的影响。

图4 电机交叉耦合动态结构图

感应电动机的交叉解耦可以通过计算消除d轴（直轴）与q轴（交轴）之间的交叉耦合电压，将定子电流d、q轴分量的控制转化成两个独立通道的单回路控制系统，以达到感应电动机的isd仅受各d轴分量影响，isq仅受各q轴分量影响的目的［7］。

3.2 基于电压型偏差解耦算法的矢量控制

针对电动机的交叉耦合，前人提出了许多解耦方法，主要有：电压型前馈解耦［8］、电压型反馈解耦［9］、基于控制理论不变性原理的偏差解耦等解耦方法。

考虑到仿真试验平台高动态性能要求，并且实际模拟阻力的计算过程存在较大的反馈延时，引入电压型偏差解耦矢量控制作为试验台的控制策略。

根据控制理论中的不变性原理，偏差解耦从电机给定电流和反馈电流的偏差处引入异步电机的外部解耦支路来抵消异步电机交叉耦合电压项的耦合作用，消除其耦合影响［10］。其原理如图5所示。

图5 偏差解耦控制原理图

根据完全解耦条件，即直轴电流isd仅受其直轴电流给定值的控制，而与异步电机的交轴电流给定值无关；交轴电流isq仅受其交轴电流给定值的控制，而与异步电机的直轴电流给定值无关。因此，可以推导得到偏差解耦型矢量控制系统解耦后的直轴电压分量udjo和交轴电压分量uqjo的关系为：

式中：

ωs——定子磁场的同步转速。

偏差解耦算法利用电机给定电流和反馈电流之间的偏差，实时地对交叉耦合项的解耦电压进行计算，避免了反馈解耦中等到电动机耦合影响产生后才进行解耦的缺陷，解决了反馈解耦中定子电流延迟对解耦电压计算的影响；同时，实时的解耦计算，消除了前馈解耦不能根据电动机实际耦合情况对电动机进行实时解耦的缺点。

4 基于LabVIEW语言的平台设计

仿真试验平台使用LabVIEW图形化编程语言对采集来的“双逆变器-双电机”系统的轴端转速、转矩信号进行显示、存储；同时，采样电机端三相电流数据，通过偏差解耦矢量控制方法对牵引电机和负载电机的转速、转矩进行控制。程序流程如图6所示。

图6 LabVIEW软件控制流程图

图6左侧所示为数据给定流程，右侧所示为数据采样、控制和存储流程。

数据给定的基本过程为：将列车自动驾驶曲线所用到的速度数据以文本形式存入计算机中，程序操作者通过指定路径可以读出该数据。文本中的数据包括两列，一列为时间，一列为速度。程序以二维数组格式读入所有数据，再通过索引函数将时间数据与速度数据分离；时间数据作为For循环的循环间隔，速度数据在循环程序中给定输出通道，进入逆变器接口。同时，程序需要给定负载电机的转矩。该转矩即牵引电机所承受的牵引力矩。程序中使用Alstom公司阻力公式结合列车惯性给出了负载电机的阻力转矩特性：

式中：

T——负载电机给定转矩，Nm；

M——一列车的总质量，kg；

R——车轮半径，m；

d v／d t——列车速度变化率；

f——列车阻力，kN；

C——齿轮传动比；

η——机械传动效率。

数据采样存储过程为：该部分采样电机轴端转速、转矩及电机电流数据。数据采集卡采集到的数据先经过软件滤波。其中，转速、转矩信号需要根据式（1）～式（4）所示的数据关系转换为原始转速、转矩值，再进入存储显示模块，可以按照一定的格式保存到文本文件中，也可以直接在操作界面中实时观测数据和波形。电机电流信号进入偏差解耦控制模块得到逆变器控制脉冲，并写入逆变器接口。

图7为该仿真试验平台设计的操作界面。

5 动态负载模拟牵引系统仿真分析

为验证方案的可行性，使用MABLAB7.1仿真软件中的simulink对实际列车上的“双电机双逆变器”交流传动进行仿真分析。

图7 动态负载模拟操作界面

为模拟实际交流传动系统，仿真中使用的电机参数与实际使用的参数完全一致，如表1所示。

表1 电机参数表

电机轴端转速给定为100rad／s，负载电机给定转矩由－300Nm切换到300Nm，切换时刻为0.2s。图8所示为牵引电机和负载电机输出转矩波形；图9所示分别为牵引逆变器和负载逆变器输入电流波形。

图8 两电机输出转矩

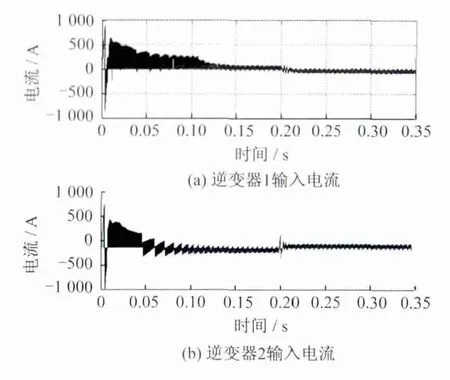
图9 两逆变器输入电流

从图8可以看出，牵引电机是主动运动，而负载电机是被动运动。因此，牵引电机在启动过程，转矩较大，需要的输入电流较大。当负载电机输出转矩稳定为－300Nm时，向母线侧输出电流，即释放能量；此时，牵引电机输出转矩稳定为300Nm，从母线吸收能量。这说明牵引电机处于电动状态，而负载电机处于发电状态，且能量在两电机之间流动。当到达0.2s切换点时，两电机的运行状态颠倒。

以上图8、图9的仿真波形说明了能量在直流母线侧实现了互馈，且可以保证两电机转速、转矩的稳定，验证了试验方案的可行性，为实物平台的试验奠定了理论基础。

6 动态负载模拟交流传动试验

根据以上理论建立了基于“双逆变器-双电机”的动态负载模拟交流传动试验平台。该平台使用2台完全相同的11kW三相交流异步电机。其额定工作频率为50Hz，额定输出扭矩为50Nm，额定输出功率为11kW，定子绕组采用380V三角形接法，额定电流为21.7A，功率因数为0.88，额定转速为2930r／min。

如图2所示，2电机用2台共直流母线结构逆变器控制，公共母线侧电压基本稳定在546V，逆变器通过LabVIEW进行偏差解耦矢量控制，并进行显示、存储等界面管理。

试验中用于给定电机的转速为南京地铁1号线某区间列车运行的实际速度数据。由于仿真试验平台所用电机输出电磁转矩的最大值为50Nm，由式（9）计算出的转矩数据需要缩小40倍后给定电机。

图10和图11分别模拟地铁单区间线路时两电机轴端转速曲线和牵引电机输出转矩曲线。该数据是从图7所示的LabVIEW显示管理界面读取的。

图10 电机轴端转速曲线

图11 牵引电机输出转矩曲线

由图11可以看出，列车启动过程经历了恒转矩、恒功率的过程，电机启动后列车基本匀速运行，因此施加在牵引电机上的转矩较小，基本为零；列车制动时以最大制动力快速制动。因此，得到的试验转矩波形符合实际地铁的运行过程。转速峰值约为2700r／min，转矩峰值约为40Nm。

图12和图13分别为牵引电机和负载电机输入电流的波形。加速起动过程中，图12牵引电机吸收电流的峰值约为17.45A，此时图13中负载电机回馈电流约为－12.58A，这说明交流传动仿真平台在加速起动过程实际从电网中吸收的电流仅为4.87A。又母线侧电压稳定在546V，因此，交流传动仿真平台在加速起动阶段最大耗能只有2.659 kW。对于制动过程，牵引电机回馈电流的峰值约为－15.98A，负载电机吸收电流峰值约为20A。这说明交流传动仿真平台实际吸收的电流最大仅为4.02A，耗能为2.19kW。由于整个过程中电机的最大转速已接近额定转速，说明两台电机都已接近额定运行状态，即输出功率11kW，但交流传动仿真平台实际从电网中吸收的功率远小于该值，说明了“双逆变器-双电机”交流传动仿真试验平台的特点。

图14为交流传动仿真平台母线的电流波形。该波形说明了交流传动仿真平台在加速起动和减速制动过程中从电网吸收的功率变化情况。从图14也可以看出，交流传动仿真平台的实际消耗功率远小于电机的额定功率。