认知无线电差分协作压缩频谱估计算法❋

陆阳❋❋

（中国电力科学研究院，北京100192）

认知无线电差分协作压缩频谱估计算法❋

陆阳❋❋

（中国电力科学研究院，北京100192）

在分布式认知无线网络场景下，针对传统协作压缩频谱估计收敛速度慢、计算复杂度高的问题，提出了一种差分协作压缩频谱估计算法用于宽带频谱感知。算法通过利用不同认知用户感知的宽带信号所满足的相同频谱支撑集特征，实现了在邻居节点感知先验信息条件下，本地认知用户基于压缩测量向量差值的宽带频谱迭代估计。仿真分析结果表明，所提算法在频谱估计精度、检测性能与计算复杂度方面均获得了明显改善。

认知无线电；协作感知；压缩感知；差分协作压缩；宽带频谱

1 引言

在认知无线电（Cognitive Radio，CR）系统中，频谱感知是次级用户（Secondary User，SU）识别“频谱空洞”，从而保证其在伺机利用空闲频段时不对授权用户（Primary User，PU）通信造成干扰的技术。然而，受无线信号在传播中的多径、阴影效应，以及SU接收机噪声与本地干扰等因素的影响，单节点的频谱感知性能往往不够理想，这使得联合多个SU感知信息融合的协作感知技术逐渐成为频谱感知的发展方向［1－2］。近年来，认知无线网络场景下针对宽带频谱的感知与处理对协作感知提出了更高的要求：宽带感知给单个SU的硬件复杂度、功耗及感知可靠性带来了极大挑战，SU射频前端的带宽扫描能力已成为制约其真正实现宽带感知的技术瓶颈；同时，复杂的无线传播环境要求SU之间须通过协作的方式引入分集增益，在提高感知性能的同时降低本地的计算量，故而高效、低复杂度的感知融合机制至关重要。

针对上述问题，本文提出了一种差分协作压缩频谱估计（Differential Cooperative Compressed Spectrum Estimation，DCCSE）算法，其核心思想在于将压缩感知（Compressed Sensing，CS）［3］用于宽带频谱协作感知，通过利用宽带无线信号因存在大量“频谱空洞”而具有的稀疏性，以亚奈奎斯特（sub-Nyquist）采样率完成信号信息的采集，从而显著降低SU的采样压力；同时，在分布式认知无线网络场景下，不同SU所感知的宽带信号具有相同频谱支撑集这一相关性特征，不同于传统算法，DCCSE实现了在邻居节点感知先验信息条件下，本地认知用户基于压缩测量向量差值的宽带频谱迭代估计，从而能够在保证协作感知性能的前提下，进一步降低感知计算的复杂度。

2 系统模型与研究现状

2.1 系统模型

假设在分布式认知无线网络场景下，PU与J个SU于网络中共存，如图1所示。其中，SU所感知的宽带信号带宽为0～B MHz，在频域可以等分为C个互不重叠的子信道，且在某一时刻，只有Q（Q≪C）个子信道被PU占用，其余C－Q个子信道空闲，宽带频谱呈现出稀疏性。假设在感知时间间隔内，宽带频谱的支撑集保持不变（即PU的频谱占用情况不变），每个SU可以通过本地压缩频谱感知算法独立获得B MHz带宽信号的频谱估计结果。

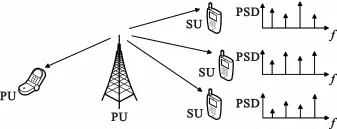
图1 分布式认知无线网络协作压缩频谱估计系统模型Fig.1 Cooperative compressed spectrum estimation system model

令PU信号为x（t），则经过独立衰落信道之后，每个SU接收到的信号rj（t）（j＝1，2，…，J）可表示为

rj（t）＝hj（t）*x（t）＋nj（t），j＝1，2，…，J（1）式中，hj（t）（j＝1，2，…，J）为PU与每个SU之间感知信道的冲激响应，nj（t）（j＝1，2，…，J）为SU接收机的白高斯噪声，*代表时域卷积运算符。若将时域信号rj（t）（j＝1，2，…，J）按照奈奎斯特（Nyquist）采样间隔Ts离散化为长度为N的序列rj＝［rj1rj2…rjN］T∈R RN（j＝1，2，…，J），则可以得到式（1）在N×N的傅里叶标准正交基Ψ＝［ψ1ψ2…ψN］下的等价频域表示为

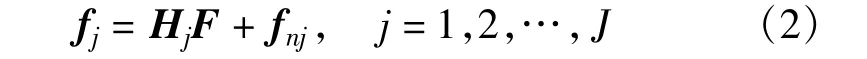
其中，fj∈C CN（j＝1，2，…，J），F∈C CN以及fnj∈C CN（j＝1，2，…，J）分别为式（1）相应部分的频域表示，Hj（j＝1，2，…，J）为N×N的信道状态信息（Channel State Information，CSI）矩阵。这里考虑SU所感知宽带频谱每个频点的信号经历独立同分布的瑞利衰落信道，即假设频点间隔大于相干带宽，则Hj（j＝1，2，…，J）为对角矩阵，表示为

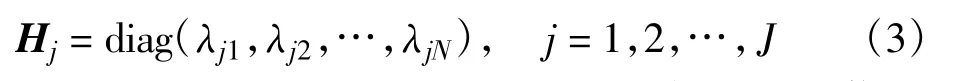
其中，λj1，λj2，…，λjN（j＝1，2，…，J）为每个频点信号的瑞利衰落系数。由于“频谱空洞”的存在，fj（j＝1，2，…，J）是稀疏的（定义其非零元素的个数为K，则K≪N），从而每个SU可基于本地压缩频谱感知算法获得各自的信号重建结果。同时，图1表明，在同样的PU信号覆盖范围内，不同SU所感知的宽带信号满足相同频谱支撑集特征，这一重要的相关性特征为本地频谱估计的协作融合奠定了基础。

令网络中每个SU均采用本地CS测量矩阵Φj∈R RM×N（K＜M≪N，j＝1，2，…，J）完成亚奈奎斯特采样，则联合式（1）和式（2），有测量向量yj∈R RM（j＝1，2，…，J）表示为

假设CSI矩阵Hj（j＝1，2，…，J）可由每个SU通过信道估计事先获知，则本地CS信号重建算法可以恢复出PU信号x（t）的频谱F，以基追踪（Basis Pursuit，BP）算法表示如式（5）所示，从而协作压缩频谱感知可等价于一类频谱估计融合问题。

2.2 研究现状

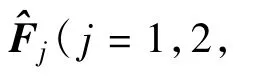
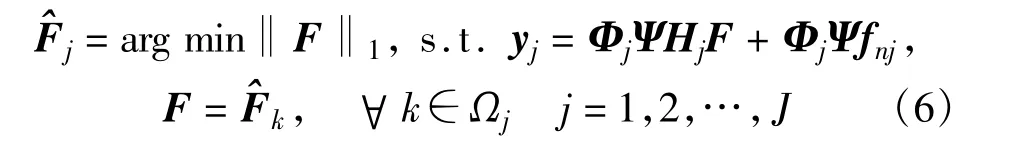
其中，Ωj（j＝1，2，…，J）为第j（j＝1，2，…，J）个SU的邻居节点集合。注意到，若SU的邻居节点较多时，式（6）的计算量较大，为此，文献［4－5］还进一步研究了改进算法。下面介绍其中一种代表性的算法。

算法1 基于一致平均约束的迭代优化

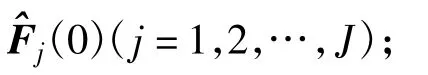
（2）每个SU执行以下迭代过程：

2）一致性平均，表示为

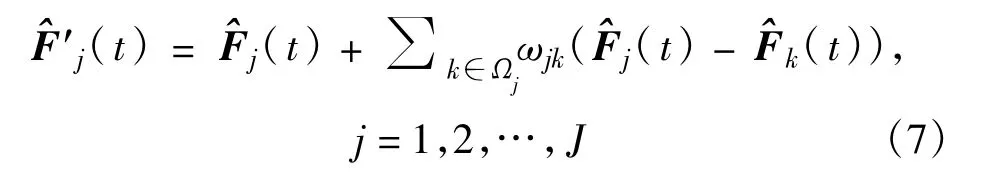
其中，ωjk为感知节点间的权重系数；

3）执行基于一致平均约束的优化，表示为

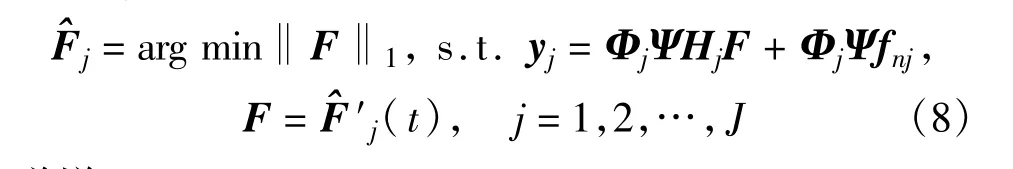
递增t＝t＋1；

可以看出，该算法通过一致性平均操作，使得在每次迭代过程中各个SU只需执行一次优化求解过程，从而大大降低了计算量。基于上述思路，文献［6－7］考虑在分布式认知无线网络场景下，PU与SU同时发射信号，并具体提出了一种基于一致性优化的协作压缩频谱估计算法。基本思想为每个SU基于CS重建宽带频谱，交替估计PU信号与其他SU的干扰，并将对PU信号的估计交换至网络中的邻居节点做一致性平均，以此为优化约束指导本地宽带信号的迭代重建，直至每个SU获得准确的频谱估计结果。

感知信道CSI已知的协作压缩频谱估计要求具有较快的收敛速度、较低的协作通信负荷以及计算复杂度，以上述基于一致平均约束的迭代优化算法为例，尚存在计算量较大的缺陷，且SU之间一致性平均权重系数ωjk选择的合适与否将直接影响融合性能，然而，其在实际情况下较难选取。由此可见，该场景下相应的高效、低复杂度融合机制仍需要进一步研究。

3 差分协作压缩频谱估计算法

3.1 算法描述

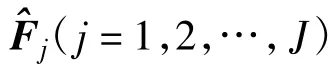
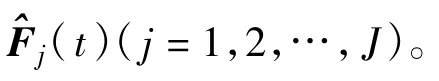
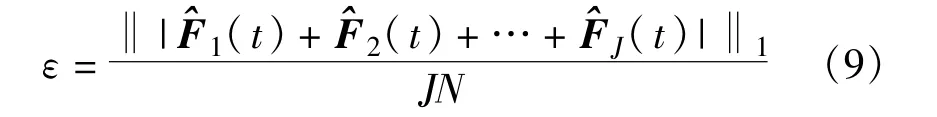
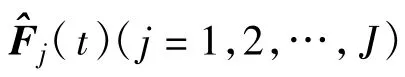
在此基础上，进而得到第1个SU经过一次差分迭代估计后在t＋1时刻恢复的频谱为

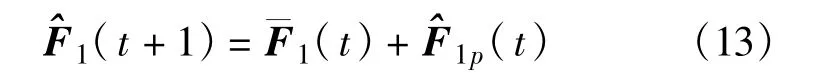
算法2 差分协作压缩频谱估计

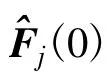
（2）每个SU执行以下迭代过程：

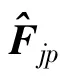
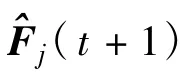
为更清楚地说明算法的迭代过程，图2给出了DCCSE算法的流程图。

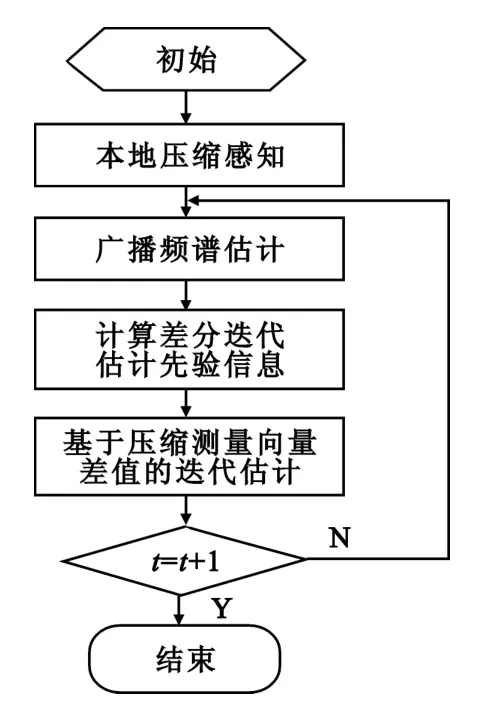
图2 DCCSE算法流程图Fig.2 The flow chart of DCCSE algorithm

频谱估计过程收敛后，进而可给出检测结果。假设SU所感知的宽带信号按照当前子信道划分，每个子信道包含U＝N/C个频点，则每个SU基于二元假设检验模型可以将其第c（c＝1，2，…，C）个子信道的“频谱空洞”判决结果表示为

其中，η是与噪声能量大小相关的判决门限，“1”代表相应的子信道被PU占用，“0”代表子信道空闲，SU可以接入。

3.2 算法讨论

本小节结合DCCSE算法具体展开讨论。

（1）算法截止条件

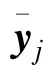
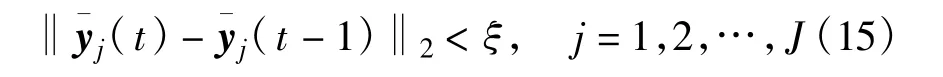
时，其中，ξ＞0为判决门限，则认为DCCSE频谱估计融合过程达到收敛状态。

（2）协作通信负荷

（3）感知计算复杂度

通过与基于一致平均约束的迭代优化算法进行对比可以看出，DCCSE每次本地迭代频谱重建过程中测量向量维数的降低，以及可以通过减少测量次数重建更稀疏的信号差值等，均能够显著降低SU的感知计算量，从而具有计算复杂度低的优势。

4 仿真与分析

本节基于蒙特卡罗（Monte Carlo）仿真给出DCCSE算法的仿真分析结果，仿真参数如下：SU感知的宽带信号带宽为100 MHz，可以等分为C＝100个互不重叠的子信道，在感知时间间隔内，只有Q＝15个子信道被PU占用，且频谱支撑集不发生变化。假设每个SU与PU之间的感知信道均服从独立同分布的瑞利衰落，频点间隔大于相干带宽，且CSI矩阵可由信道估计事先获得。定义SU本地压缩感知的压缩采样比为αCS＝M/N，其中，M代表压缩采样次数，N为信号长度。SNR定义为时域信号能量与噪声能量之比。作为反映频谱估计精度的参量，归一化均方误差（Normalized Mean Square Error，NMSE）表示为如下期望值：

（1）考察无噪声时，NMSE随着本地压缩采样比αCS、DCCSE算法迭代次数以及参与协作SU数量的变化而改变的情况，如图3所示。

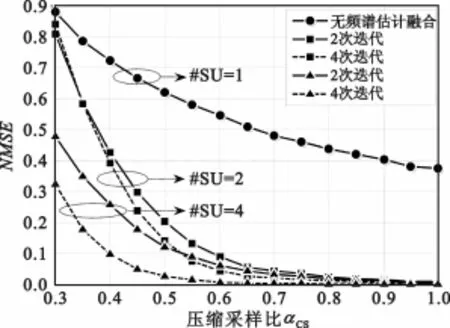
图3 DCCSE在不同压缩采样比、迭代次数及SU数量下的NMSE比较Fig.3 NMSE performance of DCCSE with varying compressive sampling ratio，iterations and the number of SUs

可以看出，采用DCCSE算法所获得的频谱估计融合结果较单个感知节点的信号恢复来说，在重建精度上有很大的提高，体现了协作分集增益对频谱感知性能的改善，且这一点在参与协作的SU数量更多时表现的更为明显。同时，本地压缩采样比αCS越大，算法迭代次数越多时，频谱估计融合效果越好。

（2）考察在不同SNR下，NMSE随着参与协作SU数量的变化而改变的情况，这里，本地压缩采样比为αCS＝0.5，DCCSE算法迭代2次，如图4所示。

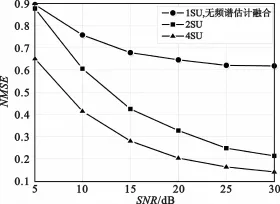
图4 DCCSE在不同SNR及SU数量下的NMSE比较Fig.4 NMSE performance of DCCSEwith varying SNR and the number of SUs

仿真结果说明了在较低的SNR下，DCCSE算法可以通过选择更多的SU参与协作压缩频谱估计，来获得频谱估计融合结果的改善。

（3）考察无噪声时，NMSE随着本地压缩采样比αCS及DCCSE算法迭代次数的变化而改变的情况。假设参与协作的SU的数量为4，为了说明基于本地测量值相减的结果只需重建更稀疏的信号差值的情况，这里在迭代过程中适当减少压缩采样比αCS，并与未减少测量次数时的频谱估计结果进行对比，如图5所示。可以看出，因为信号差值稀疏度的降低，故减少压缩采样比对信号重建精度的影响不大，且算法迭代次数越多，可以减少测量次数的比例越大，从而使得SU感知计算复杂度逐步减小，直至算法收敛。

图5 DCCSE与其测量次数减少时在不同压缩采样比及迭代次数下的NMSE比较Fig.5 NMSE performance of DCCSEwith varying compressive sampling ratio and iterationswhen themeasurements are reduced

（4）在无噪声环境下，将本文提出的DCCSE算法与文献［4］中的基于一致平均约束的迭代优化算法在频谱检测性能上进行比较，其中，后者在一致性平均过程中不同SU之间的权重系数ωjk按照文献［8］的最大度（Max Degree）准则进行选取，且算法的迭代次数均为4次。从图6中不难看出，DCCSE在协作压缩频谱估计的收敛速度上明显优于后者，也进一步验证了基于信号差值实现压缩频谱迭代估计的有效性。同时，从协作通信负荷上来看，两种算法相当；而在本地感知计算复杂度方面，由于文献［4］的算法在每次迭代过程中执行基于一致平均约束的优化时，其计算量约为O（KMN＋KN2），而DCCSE基于压缩测量向量差值的频谱重建复杂度至多为O（KMN），故本文所提算法在保证感知信息融合能够较快收敛的同时，更具有复杂度低的优势。

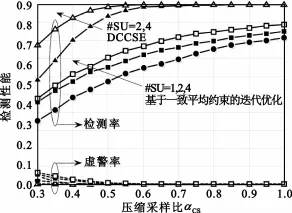
图6 DCCSE与基于一致平均约束的迭代优化算法检测性能比较Fig.6 Detection performance comparison between DCCSE and consensus averaging constrains based iterative optimization

5 结论

针对协作压缩频谱估计中感知信息的高效、低复杂度融合问题，本文研究了分布式认知无线网络场景下感知信道CSI已知的频谱估计融合机制。首先，建立系统模型并分析了传统融合策略所存在的问题；在此基础上，提出了一种差分协作压缩频谱估计算法，其理论依据在于网络中不同SU所感知的宽带信号满足相同频谱支撑集特征，通过交换SU的频谱估计至邻居节点，可在本地基于相减的压缩感知测量向量实现更稀疏的差值信号的重建，从而显著提高了频谱的估计精度，并有效降低了感知计算的复杂度。仿真结果证明了DCCSE较传统算法在协作感知性能上的提升。下一步将针对本文算法在迭代过程中压缩采样比的减少比例进行进一步研究。

［1］Ganesan G，Li Y.Cooperative spectrum sensing in cognitive radio networks［C］//Proceedings of 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks.Baltimore：IEEE，2005：137－143.

［2］Quan Z，CuiSG，Sayed AH，etal.Optimalmultiband joint detection for spectrum sensing in cognitive radio networks［J］.IEEE Transactions on Signal Processing，2009，57（3）：1128－1140.

［3］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）：1289－1306.

［4］Tian Z.Compressed wideband sensing in cooperative cognitive radio networks［C］//Proceedings of 2008 IEEE Global Communications Conference.New Orleans：IEEE，2008：1－5.

［5］曾凡仔，刘洁，李仁发，等.基于一致优化的分布式宽带合作频谱感知算法［J］.通信学报，2011，32（9）：147－152. ZENG Fan-zi，LIU Jie，LIRen-fa，etal.Distributed cooperative spectrum sensing based on consensus optimization［J］.Journal on Communications，2011，32（9）：147－152.（in Chinese）

［6］Zeng F Z，Li C，Tian Z.Distributed compressive spectrum sensing in cooperativemultihop cognitive networks［J］.IEEE Journal of Selected Topics in Signal Processing，2011，5（1）：37－48.

［7］Zeng F Z，Tian Z，Li C.Distributed compressive wideband spectrum sensing in cooperativemulti-hop cognitive networks［C］//Proceedings of2010 IEEE International Conference on Communications.Cape Town：IEEE，2010：1－5.

［8］Xiao L，Boyd S，Kim S J.Distributed average consensus with least-mean-square deviation［J］.Journalof Paralleland Distributed Computing，2007，67（1）：33－46.

陆阳（1984—），男，江苏徐州人，2012年于北京邮电大学获工学博士学位，现为工程师，主要研究方向为通信与信号处理等。

LU Yang was born in Xuzhou，Jiangsu Province，in 1984.He received the Ph.D.degree from Beijing University of Posts and Telecommunications in 2012.He is now an engineer.His research concerns communication and signal processing.

Email：luyang＠epri.sgcc.com.cn

Differential Cooperative Com pressed Spectrum Estimation for Cognitive Radio

LU Yang
（China Electric Power Research Institute，Beijing 100192，China）

In distributed cognitive radio network（CRN）scenario，this paper proposes a differential cooperative compressed spectrum estimation（DCCSE）algorithm forwide-band sensing，which can address the problems like slow convergence rate and high complexity encountered by traditional schemes effectively.Since the wide-band signals sensed by different cognitive users share the common spectrum support set，DCCSE can estimate the wide-band spectrum iteratively based on the difference of the compressed sensing（CS）measurements，with the help of the priori sensing information provided by neighboring users.Simulation results validate themarked improvements of the presented algorithm in spectrum estimation precision，detection performance and computational complexity.

cognitive radio；cooperative sensing；compressed sensing；differential cooperative compress；wideband spectrum

TN92；TN911

A

1001－893X（2013）02－0166－06

10.3969/j.issn.1001－893x.2013.02.011

2012－09－03；

2012－09－24 Received date：2012－09－03；Revised date：2012－09－24

❋❋通讯作者：luyang＠epri.sgcc.com.cn Corresponding author：luyang＠epri.sgcc.com.cn