某特种车辆液压调平系统双向液压锁动态性能仿真研究

周大星，瞿军，吕小勇

(1.海军航空工程学院研究生管理大队，山东烟台264001;2.海军航空工程学院飞行器工程系，山东烟台264001)

双向液压锁广泛应用于工程、运输、起重等机械中的油缸保压回路，能够在支腿伸出后进行油路锁定，避免发生意外情况时支脚失去控制而造成事故[1－2]。在某特种车辆中，其作用是可靠锁定调平油缸工作位置，保证车体的精确调平和保持精度。因此，深入研究双向液压锁的结构原理，分析影响其动态特性的主要因素，有利于该装置的正确使用和性能维护，确保调平系统的可靠使用。

作者利用AMESim软件建立起双向液压锁仿真模型[3－4]，对影响调平系统性能的参数:控制阀芯质量值和阻尼值、单向阀阀芯质量值和弹簧刚度值等进行了仿真，从对液压缸伸出时间和压力流量平稳性的分析中，得到影响双向液压锁动态特性的主要因素。研究并划分了液压锁故障状态，通过仿真分析，得出了故障状态临界参数。

1 双向液压锁建模

1.1 双向液压锁结构原理

双向液压锁由两个液控单向阀共用一个阀体和控制阀芯组成。液控单向阀在两端，中间有一个控制阀芯。如图1所示。

图1 双向液压锁结构

当压力油从A腔进入时，依靠油压自动将左边的液控单向阀阀芯顶开，使油液从A 流腔向A1腔。同时，通过控制阀芯把右边的液控单向阀顶开，将原来封闭在B1腔中的油液，通过B腔排出。同理，当B 油腔进油时，A 油腔就反向出油。当A、B 两腔都没有压力油时，A1腔与B1腔的反向油液依靠液控单向阀阀芯的锥面与阀体的严密接触而封闭。此时，执行元件被双向锁定[5]。

1.2 仿真模型建立[6－7]

根据双向液压锁的功能，针对一个调平油缸建立“锁－缸”执行回路，从而通过液压缸的响应特性分析液压锁的动态特性。具体建模过程有以下几个步骤:

(1)进入AMESim软件的草图模式，在Hydraulic元件库中选取相应的液压泵、液压缸和换向阀元件，构建如图2所示的仿真模型。利用HCD 库中的基本元件来构建双向液压锁模型，这样能够准确仿真其内部结构，便于深入分析影响动态特性的主要因素。

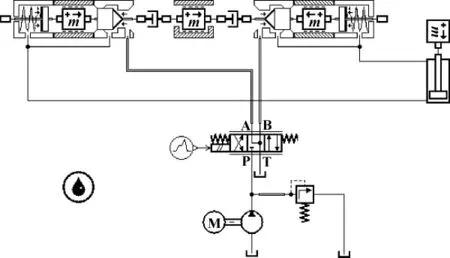
图2 双向液压锁仿真模型

(2)在子模型模式下，根据各个元件的实际类型来选取对应元件的子模型。重点选择双向液压锁的子模型种类，其他元件均选用AMESim 默认子模型。

(3)在参数模式下为各个元件设置参数。主要参数设置如表1，其他参数设置为默认值。

表1 主要参数

(4)在运行模式下，设置运行参数:仿真时间30 s，采样时间0.1 s，仿真模式为动态。

2 仿真分析

为了研究不同参数下双向液压锁的动态特性，分别对可能影响其性能的参数:控制阀芯质量值和阻尼值、单向阀阀芯质量值和弹簧刚度值进行仿真分析。

2.1 控制阀芯参数仿真分析

通过改变控制阀芯质量值，仿真得到控制阀芯不同质量下的液压缸伸出时间曲线，如图3所示;液压缸压力和流量曲线如图4所示。

图3 控制阀芯不同质量下的液压缸伸出时间

图4 控制阀芯不同质量液压缸压力和流量标准差

改变控制阀芯阻尼值，仿真得到控制阀芯不同阻尼下的液压缸伸出时间曲线如图5所示，控制阀芯不同质量液压缸压力曲线如图6所示，液压缸流量曲线如图7所示。

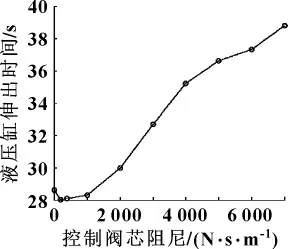
图5 控制阀芯不同阻尼下的液压缸伸出时间

图6 控制阀芯不同阻尼下的液压缸压力

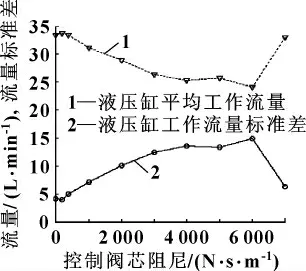
图7 控制阀芯不同阻尼下的液压缸流量

由图3可以看出:液压缸的伸出时间基本在27.9～28.2 s 之间，变化不大。当控制阀芯质量低于0.2 kg时，液压缸的伸出时间基本呈增长趋势，从27.9 s 增长到28.2 s;当控制阀芯质量高于1 kg时，基本保持在28.1 s，波动很小，表明控制阀芯质量对液压缸的伸出时间影响不大。

由图4可以看到:控制阀芯质量为0.4 kg时，压力标准差约为14.57，而阀芯质量为1.6 kg时，压力标准差增加到15.83，总体呈上升趋势，但是增长幅度不大;液压缸工作流量的标准差先是由7.30 降低到6.58，然后又上升到7.95，变化也不大。这说明控制阀芯质量对液压缸的工作压力和流量影响较小。

由图5可以看出:其他条件不变情况下，液压缸的伸出时间随双向液压锁控制阀芯阻尼增大而显著增大，并且在控制阀芯阻尼为1 000～6 000 N/ (m/s)之间近似线性增长，从约28.3 s 迅速增至约37.3 s。

由图6可发现:在控制阀芯阻尼在1 000～6 000 N/ (m/s)之间，液压缸的平均工作压力变化不大，基本在7.5 MPa 左右，而工作压力标准差基本在20左右，波动不大。

由图7可发现:液压缸的平均工作流量在控制阀芯阻尼为200～6 000 N/ (m/s)之间近似线性下降，同时，液压缸的工作流量标准差近似线性增长，速度稳定性变差。

2.2 单向阀阀芯参数仿真分析

通过改变单向阀阀芯质量值，仿真得到控制阀芯不同质量下的液压缸工作曲线，如图8所示。改变单向阀阀芯弹簧刚度值，仿真得到单向阀阀芯不同弹簧刚度下的液压缸伸出时间曲线如图9所示;液压缸压力曲线如图10所示;液压缸流量曲线如图11所示。

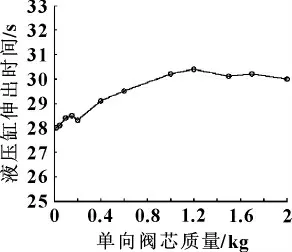
图8 单向阀阀芯不同质量下的液压缸伸出时间

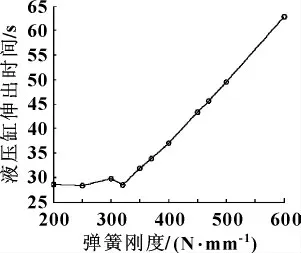
图9 单向阀阀芯不同弹簧刚度下的液压缸伸出时间

图10 单向阀阀芯不同弹簧刚度下的液压缸压力

图11 单向阀阀芯不同弹簧刚度下的液压缸流量

由图8可以看出:随着单向阀阀芯质量的增加，液压缸的伸出时间总体上呈增长趋势，阀芯质量为0.02 kg时，液压缸伸出时间最小，为28 s;阀芯质量为1.2 kg时，液压缸伸出时间最大，为30.4 s。

由图9可以看出:其他条件不变，在单向阀弹簧刚度小于320 N/mm时，液压缸伸出时间基本在28 s左右;而在320～600 N/mm时，液压缸伸出时间随弹簧刚度增大呈近似线性增大，并且增长迅速。说明弹簧刚度对液压缸性能的影响比较大。

由图10看出:在弹簧刚度小于320 N/mm时，液压缸平均工作压力有所上升，而在大于320 N/mm时变化较小。液压缸工作压力标准差在弹簧刚度小于320 N/mm时略有下降，在大于320 N/mm时基本保持在5 左右。

由图11可以看出:液压缸工作流量随弹簧刚度增加变化比较剧烈，整体上呈下降趋势，但是液压缸流量标准差随弹簧刚度变化不大，表明液压缸的伸出速度比较稳定。

2.3 双向液压锁故障仿真分析

2.3.1 故障状态划分

某特种车辆对调平性能要求为:调平精度纵向误差不大于±1.9°，横向误差不大于±1.9°;调平时间为(30 ±2)s。而调平液压缸的安装参数为:横向约5.5 m，纵向约2.4 m。假设理想情况下，地面已经水平，4个液压缸同时伸出到设计行程就能保证精确调平。但是一旦有液压缸异常工作，其伸出长度可能会达不到设计行程。因而定义调平液压缸的伸出长度误差为:在满足调平性能前提下，异常工作液压缸伸出长度小于设计行程的最大值。根据调平系统结构和安装参数可求得其值为0.08 m。

在实际使用中，液压锁常见故障为阀芯卡住、弹簧断裂、泄漏孔堵塞等[8]。这些故障均会导致工作时间的增大或者液压缸的伸出长度不够。因此设定某特种车辆的调平故障为在规定最大时间(32 s)内不能到达设计行程(0.8 m)。另外，液压缸存在缓冲和排气装置，实际中并不能完全伸长到设计行程，所以允许有不超过2%的误差(即液压缸伸出长度达到0.78 m 就视为调平到位)。

基于以上要求和设定，按照故障严酷等级将双向液压锁故障状态划分为:

无故障。液压缸伸出长度误差小于0.02 m;

轻微故障。液压缸伸出长度误差为0.02～0.08 m;

严重故障。液压缸伸出长度误差大于0.08 m。

2.3.2 双向液压锁故障仿真与分析

首先选择一组状态优良的双向液压锁性能参数作为标准参数，其具体设置如表2。设此时调平系统状态为正常状态，以阀芯卡住故障为例，通过调整不同的双向液压锁参数模拟故障，对导致轻微故障和严重故障的临界参数值进行仿真分析。

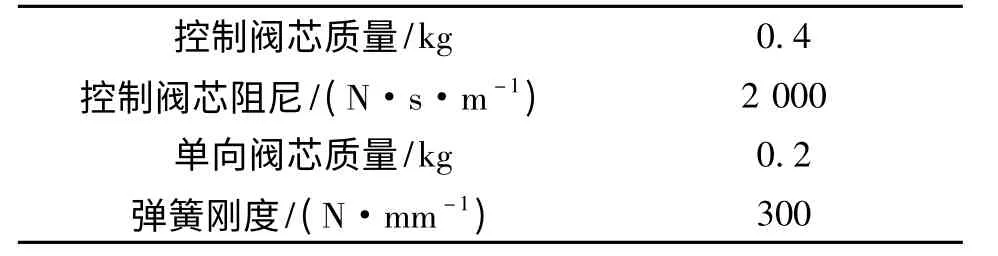
表2 标准参数

产生阀芯卡住故障的主要原因是由于阀芯与阀体配合间隙太小、阀芯受力不均或油液杂质多造成了阀芯摩擦力f 过大。保持其他参数不变，设置两端单向阀阀芯受到不同的摩擦力f，通过仿真得到液压缸伸出长度。表3是部分参数的仿真结果。

表3 部分参数仿真结果

由仿真结果可知:在单向阀阀芯摩擦力f=5.9 N时，液压缸伸出长度为0.781 m，与设计行程误差为0.019 m，可以作为产生阀芯卡住轻微故障的临界值。同理，当f=10.1 N时，液压缸伸出长度与设计行程误差为0.08 m，可以作为产生阀芯卡住严重故障的临界值。

实际情况中，阀芯摩擦力不可能为0，因此设理想状态下其摩擦力为0.02 N。对阀芯摩擦力f=0.02，5.9，10.1 N时的调平系统进行对比仿真，得到液压缸无杆腔压力和流量曲线如图12、13所示。

图12 液压缸无杆腔压力曲线

图13 液压缸无杆腔流量曲线

由以上曲线可知:随着阀芯摩擦力的增大，液压缸无杆腔的平均压力增大，平均流量减小，且压力和流量波动减小，趋向于平稳。原因是阀的开口阻力增大，开口量减小，通过阀的液压油减少，起到了节流的作用。

3 结论

(1)影响液压锁性能的主要因素是单向阀阀芯弹簧刚度和控制阀芯阻尼，控制阀芯质量和两端的单向阀阀芯质量对其性能有影响但是影响不大，见表4—7。

表4 单向阀芯弹簧刚度变化时液压缸伸出时间变化表%

表5 控制阀芯阻尼变化时液压缸伸出时间变化表 %

表6 单向阀阀芯质量变化时液压缸伸出时间变化表 %

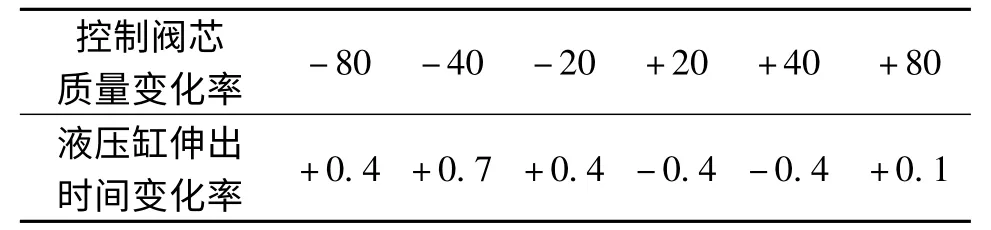
表7 控制阀芯质量变化时液压缸伸出时间变化表 %

随着控制阀芯阻尼增大，液压缸伸出时间增大，但速度稳定性变差;随着单向阀阀芯弹簧刚度增大，液压缸伸出时间增大，速度稳定性变化不大。

(2)通过双向液压锁的故障仿真，得出阀芯轻微故障的临界值为单向阀阀芯摩擦力f=5.9 N;严重故障的临界值为f=10.1 N。

【1】王春生，刘长喜，司丽丽.基于AMESim的汽车起重机双向液压锁仿真研究[J].设备管理＆维修技术，2010(2):77－81.

【2】苏东海，于江华.液压锁仿真新技术AMESim 及应用[J].计算机应用技术，2006(11):36－37.

【3】孙成通，陈国华，蒋学华，等.液压系统仿真技术与仿真软件研究[J].机床与液压，2008，36(10):140－143.

【4】方彦凯.AMESim软件在液压支架立柱系统建模及仿真中的应用[J].煤矿机械，2009，30(7):57－58.

【5】贾铭新.液压传动与控制[M].北京:国防工业出版社，2007.

【6】余佑官，龚国芳，胡国良.AMESim仿真技术及其在液压系统中的应用[J].液压气动与密封，2005(3):28－31.

【7】付永领，齐海涛.LMS Imagine.Lab AMESim系统建模和仿真实例教程[M].北京:北京航空航天大学，2011.

【8】赵静一，曾辉，李侃.液压气动系统常见故障分析与处理[M].北京:化学工业出版社，2009.