纳米金球熔化的分子动力学研究
王三军,王雪青,饶凤飞,宋友林,李金铭,王 飞
(1.河南教育学院理论物理重点学科组,河南郑州450046;2.郑州大学物理工程学院,河南郑州450001)
0 引言
金是位于元素周期表第79位的金属,是一种贵金属,在几世纪以来都被用作货币、保值物及珠宝.由于金的化学性质十分稳定,在自然界中,经常出现在岩石中的金块或金粒、地下矿脉及冲积层中.金亦是货币金属之一.在室温下为固体、密度高、柔软、光亮,其延展性及延性均是已知金属中最高的.纯金的亮黄色在传统上被认为具有吸引力.而纳米状态的金却具有很高的催化活性,在催化剂领域应用极其广泛,此外在航天、生物医学等领域也有很大应用范围[1-2].但是催化应用中的金主要为几十至上百个原子的金团簇和纳米状态金,这引起了人们很大的研究兴趣.大量实验验证,当材料的尺寸减小到纳米量级时,纳米材料的熔融性质明显低于其块体材料[3],因此金纳米团簇的熔化过程和熔点也和块体材料的金有很大的区别,在应用上也是需要考虑的一个重要内容.
然而由于实验条件、时间和空间分辨率的限制,对于纳米尺度的熔点和熔化过程很难进行细致研究.本文利用分子动力学计算模拟的方法先对金块体材料的晶格常数和平均势能随温度变化关系及熔点、弹性系数和切变常数以及径向分布函数进行了模拟计算,模拟计算得到的结果和实验符合得很好.然后构造一个Au纳米球,模拟计算了其势能随温度变化关系,利用径向分布函数和热容性质计算给出Au纳米球的熔点,还利用可视化程序研究了Au纳米球在各个温度下的熔化图像,分析讨论了Au纳米球的熔化过程.
1 计算方法
本文中所有的计算都是采用Johnson的Au的嵌入原子势(EAM),这一势的相关参数可以查询文献[4].尽管这一势函数是半经验的,它还是很好地给出了Au的一些基本特性,比如弹性常数、体模量、声子色散曲线以及单个空位和原子的扩散特性.
模拟采用周期性边界条件,计算中时间步长采取1.28×10-14s.对块体材料的计算中包含4 000个原子,模拟温度从100 K至1 400 K,每100 K取一次结果.100 K模拟开始时原子位置采用Au-FCC晶体结构设置,晶格常数a=4.08 Å,以后每一次模拟均以上一次所产生的构型为基础进行模拟计算.计算采用Verlet算法积分原子的牛顿运动方程.计算体系选用NPT系综(粒子数N、压力P和温度T不变).采用ANDERSEN等压算法[5]计算了不同温度下Fe的晶格常数以便于在有限温度下模拟时用.在构建Au纳米球的过程中,首先建立一个大小为15*a0×15*a0×15*a0(其中a0为晶格常数)的超原胞,利用命令构建一个半径为5*a0的球,去掉Au纳米球之外的原子,得到该Au纳米球中的原子数目(2 112个)和坐标.在以下的模拟
2 结果和讨论
2.1 Au块体材料性质的计算
在图1中我们给出计算得到的Au块体材料的晶格常数、原子平均势能与温度的变化关系.由图1可以看出,Au的晶格常数、原子平均势能与温度的变化基本上呈现单调递增关系,但在1 350 K后有一个较大的变化,表明体材料在这里出现了某种构型上的变化,可以认为发生了相变,即由固态向液态的转变.
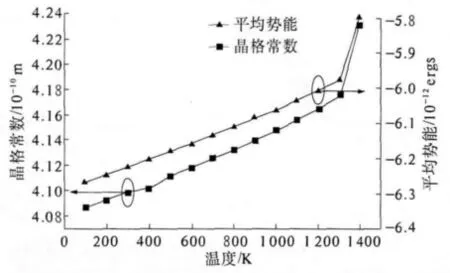
图1 晶格常数、平均势能与温度变化关系曲线,其中,含“■”线代表晶格常数随温度变化图,含“▲”线代表平均势能随温度变化图Fig.1 Calculated lattice constant and average potential as a function of temperature.The square-line is the lattice constant and the square line is the average potential
如图2所示,我们分别给出了0 K、300 K、800 K、1 100 K、1 200 K、1 300 K、1 400 K时的径向分布函数(RDF).可以看出,随着温度的增加,Au的径向分布函数有着很大的变化.在1 300 K以下,固定距离上径向分布函数都有明显的峰,当温度达到1 400 K时Au的径向分布函数已经相当平缓,观察不到峰,结合前面所得到的Au的晶格常数与平均势能随温度的变化关系图,可以认为其熔点在1 300 K到1 400 K之间,即为1 350 K左右.实验中,Au的熔点正是1 337 K,符合得很好.
2.2 Au纳米球性质的计算
利用上述方法得到纳米球后,分别模拟计算各个温度下的原子平均势能.起始温度设为300 K,以后每100 K取一次值,直到1 500 K.时间步长仍然为1.28×10-14s.在每一次的计算过程中,都采取弛豫平衡的办法,即每一个温度下的计算都重复5 000步,得到其平衡平均势能.最终结果如图3.

图2 不同温度下面心立方Au的径向分布函数(RDF)Fig.2 The RDF of FCC Au at different temperature
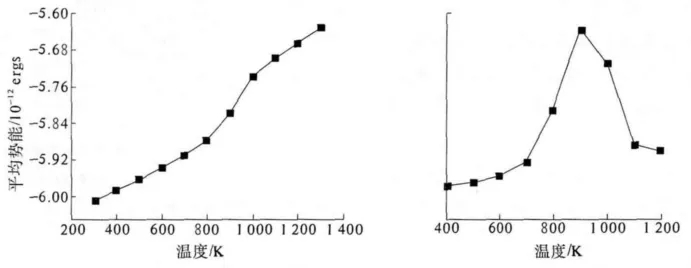
图3 纳米Au球中原子平均势能(左)和热容(右)随温度变化关系Fig.3 The average potential(left)and heat capacity(right)of nano sphere Au at different temperature
由图3可以看出,对于Au纳米球来说,平均势能随温度的变化呈现单调递增的关系,即温度越高平均势能越高.只是在900 K左右出现一个较大的变化,说明纳米球在这里出现构型变化,即出现了由固态向液态的转变.对比图3右图的热容随温度的变化关系,可以认为该纳米球的熔点为900 K左右.
下面计算该纳米球的径向分布函数RDF,并将前面图2中得到的Au体材料的RDF相对比.在计算RDF的时候,晶格常数取为图1中与温度分别对应的值.考虑上面原子平均势能随温度的变化中,在900 K左右,势能曲线有一个转变,这里分别计算纳米Au球800 K、900 K时的RDF,并与体材料800 K、900 K的RDF相比较,对比图如图4.

图4 纳米Au球与Au体材料RDF变化对比图Fig.4 The RDF of nano sphere Au and bulk Au at 800 K and 900 K
根据图4对比可以得到,800 K温度下,纳米球与体材料的RDF基本上一致,说明虽然二者的体形状不同,但其构型是一致的,均有4个主峰和2个小峰,没有结构形变的发生;而900 K温度下,纳米球的RDF相对于体材料发生了很大变化,体现在体材料横坐标6.8 Å处的峰值并未出现在纳米球的RDF曲线中,说明此时纳米球的结构发生了变化,即此时纳米球开始熔化.结合上一部分分析得到的结果,可以认为构建的纳米Au球的熔点为900 K.
从前部分可以得到文中所构建的纳米Au球熔点为900 K左右.利用可视化子程序可以得到不同温度下纳米Au球的模拟熔化图像.根据这些图像,可以更直观地得到有关熔化过程的信息.
为了对比方便,分别将纳米Au球300 K、800 K、850 K和900 K时的熔化模拟图像进行对比,在图像的选择中,将纳米球分成11个薄层,对比图像选取最中间的第6层进行作图显示,所得模拟图像如图5所示.可以看出,300 K即室温下,纳米Au球中的原子只在平衡位置附近振动,即体系保持正常的晶体结构;800 K温度下纳米球表面的某些原子开始出现无序化,但体系中大部分原子都保持正常的晶体结构;850 K时纳米球表面层原子已经完全无序化,只有中心部分原子保持晶体结构;900 K时,模拟进行5 000步时,中心原子只在平衡位置振动,但已经有中心附近的原子突破平衡位置束缚,模拟进行到20 000步时,体系整体无序化,此时纳米球已经熔化,不再具有有序的晶格结构.另外通过以上图像可以发现纳米Au球在熔化过程中是由外到内逐层熔化的,这与文献[6]得到的结果相符.
3 结论
本文利用分子动力学计算机模拟方法模拟计算了面心立方Au晶体的晶格常数、熔点、RDF并对比研究了Au纳米球的熔点等物理性质,得到了以下结论.

图5 不同温度下纳米Au球熔化模拟图像(20 000步)Fig.5 The simulated configuration of melt progress for the nano sphere Au at different temperature
(1)利用嵌入原子势(EAM)得到了Au晶体在不同温度下晶格常数和原子平均势能随温度的变化关系,结合Au晶体的RDF分布得到了Au的熔点为1 350 K左右,与实验值1 337 K符合得很好.
(2)构建了一个直径4 nm包含2 112个原子的Au纳米球,计算给出了该纳米球的原子平均势能随温度变化的关系,发现在900 K左右有一个突变;进一步计算了纳米球的RDF并将之与Au晶体体材料的RDF进行比较,确定该纳米Au球的熔点在900 K.
(3)利用可视化子程序得到了所构建的Au纳米球在各个温度下的熔化模拟图像,直观地观察了熔化过程,发现纳米Au球在熔化过程中是由外到内逐层熔化的.
[1] WALTER M,AKOLA J,LOPEZ-ACEVEDO O,et al.A unified view of ligand-protected gold clusters as superatom complexes[J].Proc Natl Acad Sci U S A,2008,105(27):9157-9162.
[2] REVELES J U,CLAYBORNE P A,REBER A C,et al.Designer magnetic superatoms[J].Nature Chemistry,2009,1(4):310-315.
[3] SHIM J H,LEE B J,CHO Y W.Thermal stability of unsupported gold nanoparticle:A molecular dynamics study[J].Surf Sci,2009,512(3): 262-268.
[4] JOHNSON R A.Phase stability of fcc alloys with the embedded-atom method[J].Phys Rev B,1990,41(14):9717-9720.
[5] ANDERSEN H C.Molecular Dynamics simulations at constant pressure and/or temperature[J].J Chem Phys,1980,72(4):2384-2393.
[6] 张妍宁,王丽,边秀房.中介尺度Au纳米团簇熔化的分子动力学模拟[J].物理化学学报,2003,19(1):35-39.
——《势能》

