基于熵值法的改进集对分析水质模糊评价

郑志宏，魏明华

(1.华北水利水电学院环境与市政工程学院，河南郑州 450011;2.华北水利水电学院水利学院，河南郑州 450011)

近年来随着经济的高速发展，不但在水量方面出现了供需矛盾，而且由于各种工业废料、农业化学物质的排放，造成了河流、湖泊、水库等地表水水质严重恶化，直接影响着经济社会的可持续发展。因此，客观评价水质状况关系到人类在内的整个生态系统的健康和安全。目前，水质综合评价方法很多，如层次分析法［1］、灰色关联法［2-3］、模糊评判法［4］、人工神经网络法［5］、理想区间法［6］、物元分析法、属性识别法［7］和主成分分析法［8］等，各种方法均有其各自的优缺点和使用条件，尤其在评价指标的权重确定方面都存在很大的困难。笔者通过应用基于熵值法的改进集对分析模糊评价方法，以滦河下游唐山地区7个代表性测站为研究实例，对滦河下游河流水质状况进行评价，得到符合实际的综合评价结果。

1 熵值法原理

在信息论中，信息熵H(x)=-∑p(xi)lnp(xi)反映系统的无序化程度，信息熵越小，系统的无序化程度越大，信息熵越大，系统的无序化程度越小。熵值法就是利用信息熵这一理论工具，根据各项指标值之间的差异程度，计算出各指标的权重，为多指标综合评判问题提供依据。熵值法是一种比较客观的赋权法，这种方法避免了人为因素带来的偏差，并且在众多客观赋权法中是计算较简单的一种［9］。熵值法的计算步骤如下:

设有m个采样点、n项指标［10］，构成原始数据矩阵X=(xij)m×n。

a.对xij归一化处理:

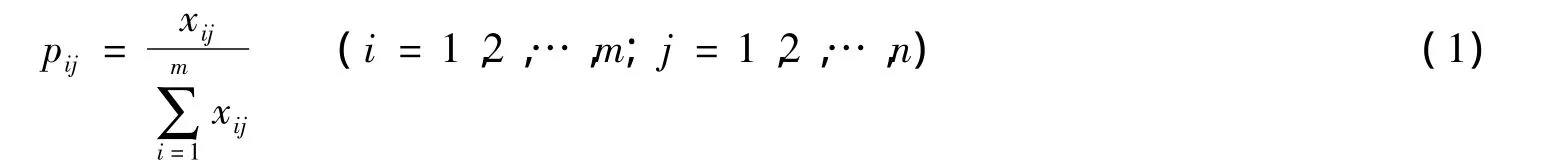
b.计算第j项指标的熵值:

c.计算第j项指标的权重。对于给定的j，指标的权重越大，所揭示的测评指标的差异越大，测评指标的熵值越小，因此令

对uj进行归一化处理，使∑wj=1。则第j项指标的权重，这样就能得到多目标评判问题各项指标的权重，从而可以利用各种综合评判的方法进行评价。

2 集对分析方法改进

集对分析(set pair analysis，SPA)是赵克勤在1989年提出的一种新的系统分析理论方法［11-12］。该评价方法存在的不足之处为b，c的细化问题，同异反评语细化问题。如地表水水质评价中存在5类水质标准;一个方案指标的评价语有“好、一般和差”，在好中也有“稍好、好、很好、极好”等细化差别;同样差也有“稍差、差、很差、极差”等细化差别。虽然有学者对这类问题用贴近度来处理［13］，但结果仍不甚理想。笔者对其进行如下改进。

设有n个评价指标，将地表水环境指标的各个等级标准Ap={vp1，…，vpk，…，vpn}分别组成一个集合，p表示等级，将每个区域的地表水环境指标数值系列Bq={xq1，…，xqk，…，xqn}分别组成另一个集合，q表示区域，这2个集合构成一个集对(Ap，Bq)。比较2个集合中的对应项xqk和vpk，若xqk处于vpk的评价级别中，则认为是相同。若xqk处于vpk的相邻级别中，且在评价级别优越一边，则认为是优异，其值简记为b1;若xqk处于vpk的相邻级别中，且在评价级别劣差一边，则认为是劣异，其值简记为b2。若xqk处于vpk的相隔级别中，且在评价级别优越一边，则认为是优反，其值简记为c1;若xqk处于vpk的相隔级别中，且在评价级别劣差一边，则认为是劣反，其值简记为c2。这样，b，c得到进一步细化，并且这样处理符合原创联系度可展性。具体评价模型见文献［14］。

3 基于改进集对分析模糊综合评价

模糊综合评价是以模糊数学为基础，对受多种因素制约的不确定性问题进行定量化描述的一种方法。基于集对分析的模糊综合评判的一般步骤如下［15］:

a.确定评价对象的因素(指标)集合U={u1，u2，…，un}，共有n个因素。

b.确定备择集(或评语集)V={v1，v2，…，vm}，共有m个因素。

c.确定权重向量W=［w1，w2，…，wn］为U中各因素对待评事物的隶属关系。权重集表示各影响因素在评判过程中所占的重要性程度。

d.进行单因素评判，建立因素论域和备择论域之间的集对分析联系度矩阵R。

e.选择合成算子，将W与R合成得到B，其基本模型为B=W◦R，“◦”为模糊乘运算算子。

f.取集对势最大者为待评方案对应的评判等级。

4 基于熵值法改进集对分析水质模糊评价计算

4.1 数据选取

选取滦河下游唐山地区7个监测站点2003年的地表水监测指标，分别为冷口(S1)、崖口(S2)、邱庄水库(S3)、小定府庄(S4)、陡河水库(S5)、石佛口(S6)、滦县(S7)。取溶解氧(x1)、氨氮(x2)、高锰酸盐(x3)、氟化物(x4)4项指标作为研究对象，分级标准如表1。

4.2 熵值法确定指标权重

a.建立原始数据矩阵:

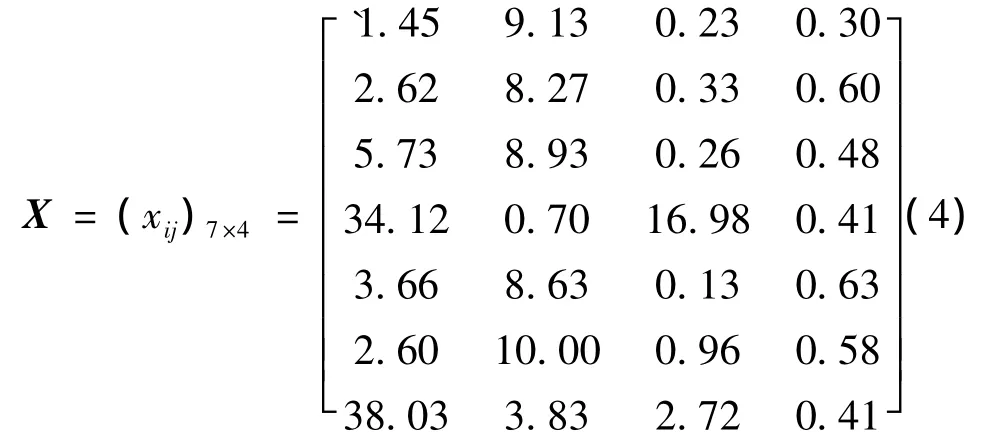
表1 地表水分级标准Table 1 Surface water quality criterion grades mg/L

b.按照式(1)进行数据转换得到X'=(pij)7×4。

c.计算第j项指标信息熵。

d.计算第j项指标权重，得到指标权重向量为W=［w1，w2，w3，w4］=［0.178，0.410，0.244，0.168］。

4.3 改进集对分析模糊综合评价

a.建立S1监测站点的联系度矩阵:

b.应用Matlab计算软件对S1点进行模糊运算:

因此shi(A)=a/c或 shi(A)=a/b，shi(u1)=10.779，shi(u2)=1.382，shi(u3)=0.956，shi(u4)= 0.929，shi(u5)=0.384。

分别计算5级集对势，得到S1监测站点从Ⅰ级到Ⅴ级的概率分布为:74.7%，9.6%，6.6%，6.4%，2.7%。所以，得到S1监测站点的评价结果为Ⅰ级。同理，可得到其他6个监测站点的评价结果(表2)。

分别取各监测站点集对势计算结果最大值所在等级为评价结果等级，可得到评价结果如下:S1，S2，S3，S5和S6监测站点为Ⅰ级;S4，S7监测站点为Ⅴ级。

5 结 语

使用相同的数据进行计算，综合指数法的评价结果如下:S1，S2，S3，S5，S6监测站点为Ⅰ级;S4，S7监测站点为Ⅴ级。该结果与本文方法评价结果一致，符合度达到100%。灰色关联法评价结果如下:S1，S2，S3，S5，S6监测站点为Ⅰ级;S4监测站点为Ⅴ级;S7监测站点为Ⅳ级，该结果与本文方法的评价结果符合度达到85.7%，评价结果只在S7监测站点有略微差异，与其余6个监测站点的结果基本一致。以上结果证明了基于熵值法的改进集对分析模糊综合评价模型具有合理性。另外，该方法利用信息熵来确定指标权重，相对来讲更客观，克服了单纯主观赋权方法的人为因素干扰，使评价结果更贴近实际情况，且整个模型计算过程简单便捷，有很好的应用价值。

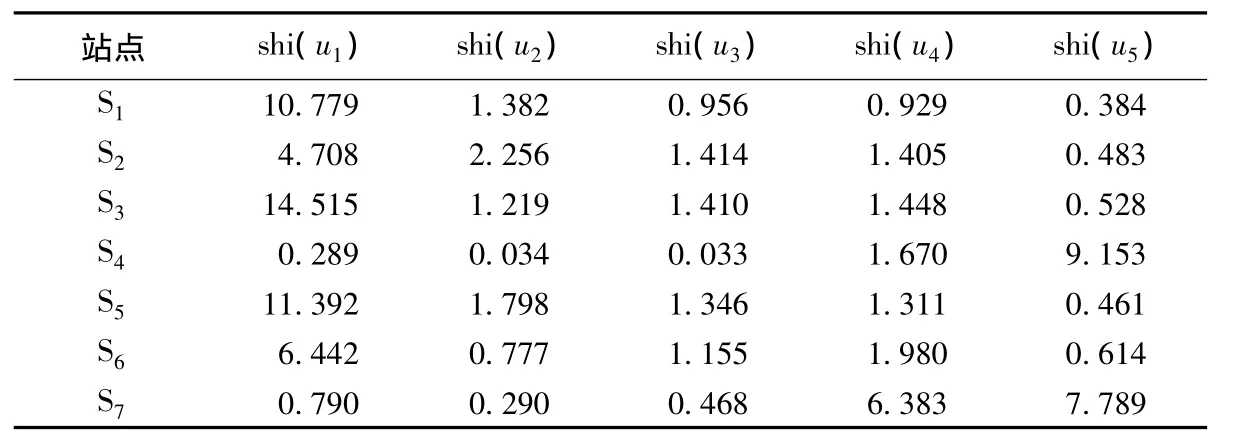
表2 各监测站点评价结果Table 2 Evaluation results of monitoring sites

［1］刘章军，叶燎原.模糊概率模型及其在地下水水质评价中的应用［J］.应用基础与工程科学学报，2007，15(3):286-293. (LIU Zhangjun，YE Liaoyuan.Fuzzy probability model and its application to evaluation of groundwater quality［J］.Journal of Basic Science and Engineering，2007，15(3):286-293.(in Chinese))

［2］刘思峰，党耀国，方志耕.灰色系统理论及其应用［M］.北京:科学出版社，2004:121-126.

［3］程诚，李春杰.灰色关联分析在区域电力市场效率评价中的应用［J］.华北电力大学学报:社会科学版，2010(3):10-13. (CHENG Cheng，LI Chunjie.Application of grey incidence analysis in the regional electricity market efficiency evaluation［J］. Journal of North China Electric Power University:Social Sciences，2010(3):10-13.(in Chinese))

［4］郑志宏.郑州市地下水环境评价及修复研究［D］.郑州:华北水利水电学院，2007.

［5］韩立群.人工神经网络理论、设计及应用［M］.北京:化学工业出版社，2001:55-78.

［6］杨晓华，杨志峰，沈珍瑶，等.城市环境质量综合评价的多目标决策理想区间法［J］.系统工程理论与实践，2005，25(8): 119-123.(YANG Xiaohua，YANG Zhifeng，SHEN Zhenyao，et al.A multi-objective decision-making ideal interval method for integrated assessment of urban environmental quality［J］.Systems Engineering-theory＆Practice，2005，25(8):119-123.(in Chinese))

［7］王硕，张礼兵，金菊良.系统预测与综合评价方法［M］.合肥:合肥工业大学出版社，2006:75-98.

［8］王静龙.多元统计分析［M］.北京:科学出版社，2008:102-136.

［9］柯蓉.熵值法在综合评判股市多指标中的应用研究［J］.经济论坛，2006(14):107-124.(KE Rong.The application research of entropy method in comprehensive evaluation stock market index［J］.Economic Tribune，2006(14):107-124.(in Chinese))

［10］王元华，曾凤章.基于熵值法的顾客满意度测评［J］.商业研究，2004(22):11-13.(WANG Yuanhua，ZENG Fengzhang.An evaluation method of customer satisfaction degree based on information entropy［J］.Commercial Research，2004(22):11-13. (in Chinese))

［11］赵克勤.集对分析及其初步应用［M］.杭州:浙江科学技术出版社，2000:1-3.

［12］邓红霞，李存军，朱兵，等.基于集对分析的生态承载能力综合评价方法［J］.长江科学院院报，2006，23(6):35-38. (DENG Hongxia，LI Cunjun，ZHU Bing，et al.Integrative assessment of eco-carrying capacity based on set pair analysis［J］. Journal of Yangtze River Scientific Research Institute，2006，23(6):35-38.(in Chinese))

［13］周超明，晏路明.港湾水质综合评价的集对分析模型［J］.环境科学与管理，2006，31(8):62-66.(ZHOU Chaoming，YAN Luming.A module of set pair analysis on the comprehensive assessment of seawater quality of harbors and bays in Fujian Coast［J］.Environmental Science and Management，2006，31(8):62-66.(in Chinese))

［14］魏明华，郑志宏，黄强，等.基于改进SPA法的地下水环境模糊综合评判［J］.水利学报，2009，40(10):1204-1209.(WEI Minghua，ZHENG Zhihong，HUANG Qiang，et al.Fuzzy comprehensive evaluation of groundwater environment based on improved set pair analysis［J］.Journal of Hydraulic Engineering，2009，40(10):1204-1209.(in Chinese))

［15］姜军，宋保维，潘光，等.基于集对分析的模糊综合评判［J］.西北工业大学学报，2007，25(3):421-424.(JIANG Jun，SONG Baowei，PAN Guang，et al.A novel method for fuzzy comprehensive evaluation based on set pair analysis［J］.Journal of Northwestern Polytechnical University，2007，25(3):421-424.(in Chinese))