基于数字变极化探测系统目标极化散射特性研究

赵国强 李璋峰 孙厚军 吕 昕

（北京理工大学信息与电子学院，北京100081）

引 言

传统的单脉冲探测器大多采用和差网络或者中频和差电路来获得和差信号，所带来的问题是引入了差损，使雷达系统中接收机的噪声系数恶化、通道间的幅度相位一致性不易测量和校准，以及无法兼容更多的波束修正算法等.同时，传统的多脉冲探测器多采用固定极化、收发同极化的方式获取目标信息，目标识别只能采用高分辨距离像及散射中心等方法，丢失了极化域的信息，容易受到干扰和假目标的欺骗.

随着数字技术及收发组件小型化技术的不断发展，可以利用多通道系统、数字波束形成、变极化等新技术，克服上述问题.

数字变极化单脉冲探测技术是在信号处理模块得到和差信号，发射时在空间完成极化合成，接收时采用“虚拟极化”的方法对各通道进行幅相加权处理，获得回波中的极化信息.该系统可用于目标、杂波等多极化、全极化特性研究实验.同时，近些年来，极化散射熵的原理被广泛应用于各种极化雷达系统，如星载极化合成孔径雷达［1-5］，其属于一类重要的极化信息.

本文主要针对数字变极化单脉冲系统中的全极化信息获取，简要介绍和分析数字变极化的原理和实现、基于频率步进信号的高分辨一维距离像的合成，以及获得极化散射熵H和平均散射角α在距离像中的分布，并分析其在地杂波背景下用于目标检测和识别的可行性.

1 数字变极化探测原理

1.1 数字变极化单脉冲探测系统组成

此处给出数字变极化单脉冲系统简单的原理组成框图，如图1所示.

图1 四子阵变极化单脉冲系统原理框图

通过对信号发生模块和幅相控制模块的调整，可以实现发射通道的校准和各种发射极化形式的合成；通过数据采集和处理模块，可以对各路回波数据进行幅相加权，实现接收通道校准和“虚拟极化”接收.

1.2 基于四单元线极化子阵的极化合成原理

变极化单脉冲系统实现的关键在于得到单脉冲天线和差波束，同时形成对天线极化的控制.系统的天线是一种基于四个线极化子阵的变极化平面阵列天线.该天线由四个线极化子阵组成，各子阵呈扇形旋转对称结构，极化方向为斜45°和135°，如图2所示.发射时，通过控制各子阵的馈电幅度和相位实现不同的发射极化形式，即图中的幅度An和相位φn（n＝1，2，3，4）.实现线极化和圆极化发射形式（传播方向垂直纸面向外）的幅相关系如表1所示.

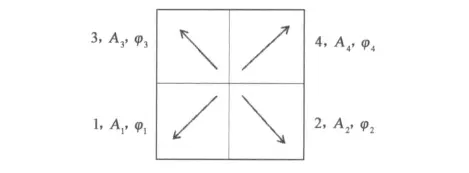
图2 四子阵变极化天线示意图

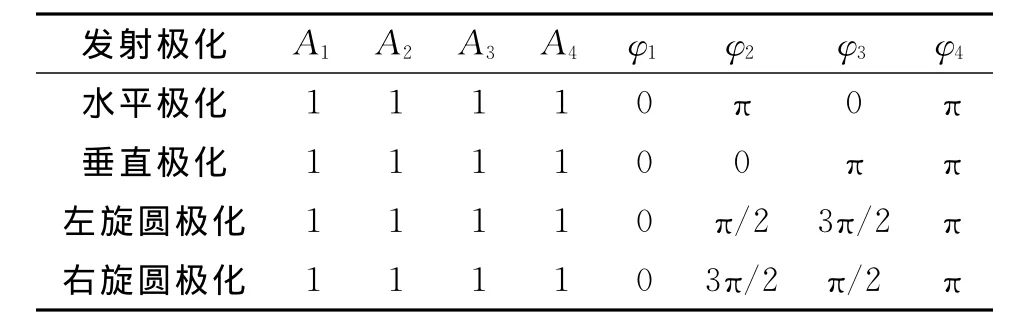
表1 各种发射极化的幅相加权关系

接收时，采用虚拟极化的方法对各子阵的接收信号进行基带幅相加权，得到不同的接收极化（如水平、垂直线极化等）.

以发射水平极化形式，虚拟极化接收水平和垂直极化为例，说明是如何对各通道回波数据进行幅相加权的.发射水平极化形式时，四个天线子阵的极化形式可用图2中实线箭头来表示，而虚线箭头表示回波中的水平分量和垂直分量.

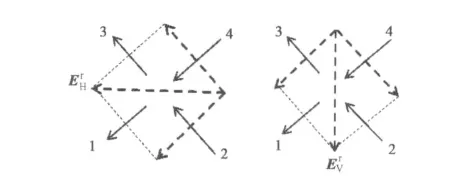
图3 发射极化和接收分量的简要表示

设回波中的水平和垂直分量分别为ErH、ErV，Rn表示第n个通道接收到的回波，那么：

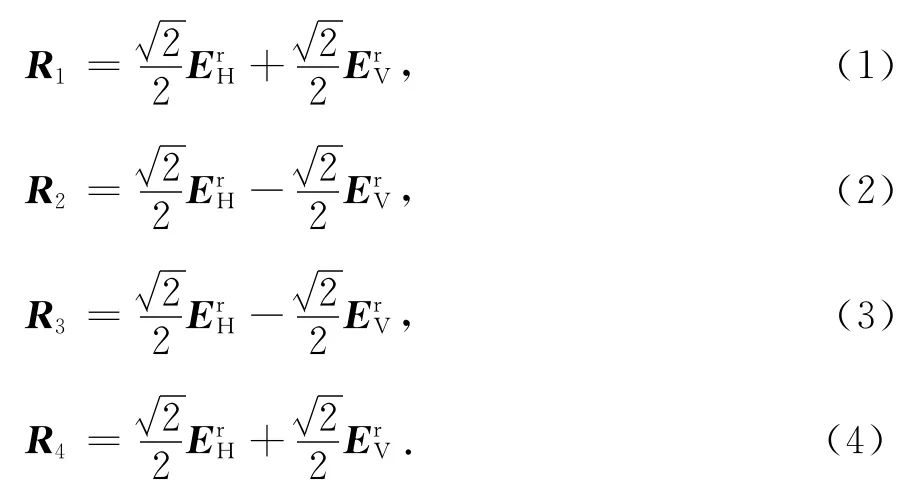
RH、RV分别表示“虚拟接收”的水平极化分量和垂直极化分量，有：

式（5）和式（6）表明：在发射水平极化形式的情况下，将四个通道接收的回波数据相加，可以得到回波中的水平分量；先对2、3通道接收的数据进行-π的相位加权，再将四个通道数据相加，可以得到回波中的垂直分量.

1.3 高分辨一维距离像的原理

系统中采用频率步进信号体制，通过对脉冲回波的逆快速傅里叶变换（Inverse Fast Fourier Transform，IFFT）分析处理，获得距离高分辨的效果［6］.

设频率步进信号脉冲重复周期为Tr，脉冲宽度为τ，起始频率为f0，步进为Δf，频率步进数为N，光速为c.频率步进发射信号为［7］

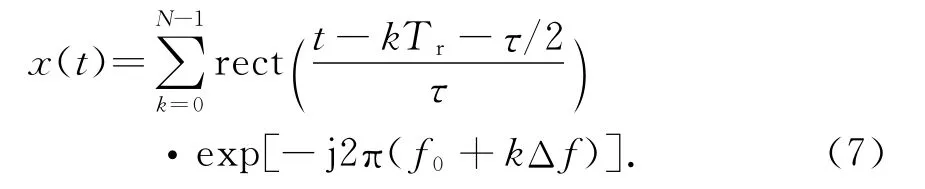
本振信号为

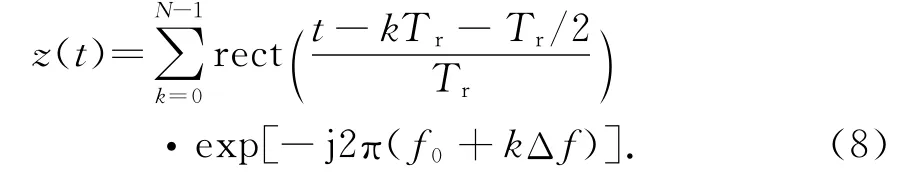
距离为R的目标回波信号为

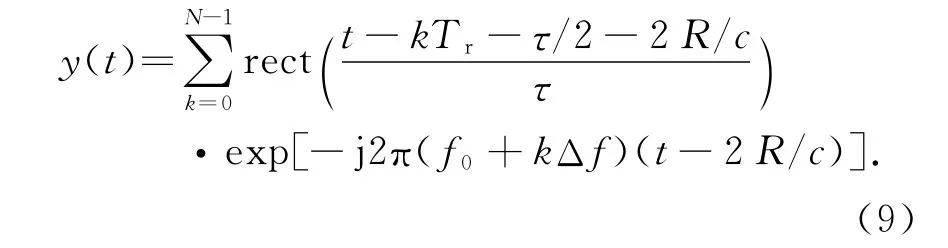
回波信号与本振混频后得到

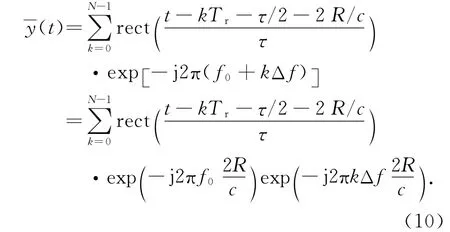
式（10）中，第一个指数项是常数，第二个指数项可以看成一个频域函数，对其作IFFT运算并求模，可以得到高分辨距离像.

对于数字变极化单脉冲系统，合成正交极化形式分时发射，对四个子阵接收数据虚拟极化合成得到同极化和交叉极化接收回波，可以得到目标的全极化回波，结合上述原理，对全极化回波进行IFFT处理，可以得到目标的全极化高分辨一维距离像.

1.4 极化散射熵的概念

目标极化分解理论是雷达极化学中重要的理论之一，当前的极化理论大体分为两类：一类称为相干极化分解，包括Pauli基分解［8］、Krogager分解［9］及Cameron分解［10］，其基本原理是将目标极化散射矩阵分解成几类基本散射体（如球体、二面角、三面角等）的线性组合；另一类是基于目标极化散射二阶统计特性的非相干分解，如S.R.Cloude通过对目标极化相干矩阵特征值分解，提出的著名H/α极化分解［11］，A.Freeman提出的“奇次-偶次-漫散射”分解方法［12］等.

熵是描述自然界混乱的程度，1997年，Cloude将“熵”的概念引入极化理论中，定义了散射熵H和平均散射角α，用于目标的散射特性分析.

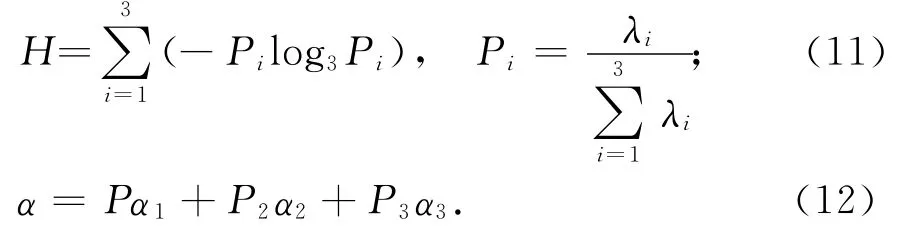
H的值在［1，0］之间，描述了目标散射的随机性.H＝0时，相干矩阵只有一个特征值不为0，目标只有一种主要散射机理，此时处于完全极化状态；H值较低时，三个特征值中有一个较大，其余两个很小以致可以忽略，目标接近完全极化；随着H的增大，去极化程度增加，说明目标散射由几种散射过程组成，不再认为仅存在一个占主要地位的散射机理；当H值较高时，三个特征值比较接近，目标接近完全非极化；在H＝1的极限情况下，所能获得的极化信息为0，目标的散射完全随机，处于完全非极化状态［11，13］.

α在0°和90°之间，反映了目标的主要散射机理.当α＝0°时，表示目标的主要散射机理是各向同性的表面散射，如平静水面或者均匀导体球的散射；随着α的增加，反映出的散射机理变为各向异性的表面散射，如布拉格表面散射；当α＝45°时，表示偶极子散射模型，如来自一片各向异性微粒的散射；在α＝90°的极限时，表示二面角散射［11，13］.

对于地表背景下有人造目标的情况来说，地表的去极化效应相对人造目标要大，即地表的极化散射熵比人造目标的熵值高，同时，人造目标多由平坦的表面和尖锐的棱角（如二面角），即平均散射角多接近0°和90°，而天然目标则不存在这些特性，这些区别就可以应用于在地杂波背景下的目标检测与识别.

2 实验和分析

我们对地面二面角和卡车目标进行了实验.照射角度、卡车摆放姿态和地表背景如图4所示.卡车车长6m，实验采用频率步进信号，步进Δf＝5MHz，频率步进数N＝128，分辨率约为0.23m.

图4 实验场景

分时发射水平极化和垂直极化波时，“虚拟极化”合成同极化和交叉极化接收，处理回波数据得到线极化基下全极化高分辨一维距离像.调整各子阵间馈电的相位差，分时发射左旋圆极化和右旋圆极化，可以得到圆极化基下全极化高分辨一维距离像.同时，对两种发射极化形式下获得的全极化数据进行极化散射熵H和平均散射角α的提取，得到其在高分辨距离的分布（图中所示为波门内的高分辨距离），如图5和图6所示.

图5中实线是二面角极化散射熵，图5（a）中的虚线是二面角高分辨距离像（High Resolution Range Profile，HRRP），图5（b）中的虚线是平均散射角.从图5（a）中发射线极化情况下散射熵值H在高分辨距离的分布可以看出：在22m处左右，散射熵值明显低于其他的距离范围，其对应着高分辨距离像中的尖峰处，即二面角目标.从图5（b）中发射圆极化情况下极化散射熵H和平均散射角α在高分辨距离中的分布可以看出：在22m处，具有极低熵值，较高的平均散射角，根据文献［11］中关于散射熵和平均散射角九个区的划分，可认为其处于低散射熵的多次散射区（二面角）和部分的平面散射区.

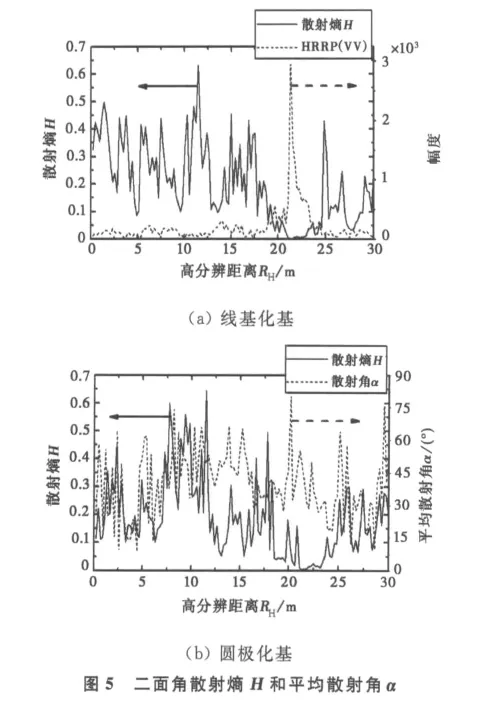
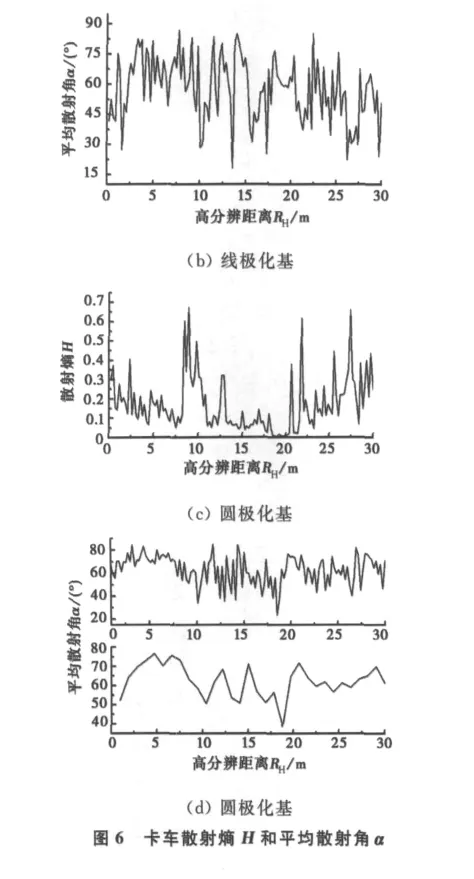
图6（a）中的虚线是卡车HH通道高分辨距离像.从图6中两种发射极化的散射熵值H在高分辨距离的分布可以看出：约在12～21m的目标卡车范围内，熵值较其他区域明显偏低，特别在19m处左右，熵值达到最小，对应于高分辨距离像中的最高峰，其对应于卡车车头的强散射中心.从两种发射极化的平均散射角α在高分辨距离中的分布可以看出：在12～21m的范围内，α值的起伏比其他范围更大，这是由于卡车多有平坦的表面和二面角，即α为0°和90°，所以，在这个范围内的平均散射角α多为靠近0°或90°的值，从而导致α值起伏较大.图6（d）中，对圆极化发射形式下的平均散射角α值对高分辨距离单元相邻4个做平均（图6（d）中下图），其更清楚地反应了上述情况.

3 结 论

极化信息是目标回波中重要的信息，本文基于数字变极化探测系统，结合高分辨距离像和极化散射熵的相关原理，对地面目标回波中的极化散射熵进行了提取以及相应的分析，说明了该类极化信息提取在地面目标检测和识别中的可用性.

实验的地表背景并不是很复杂，下阶段实验中将在多种地形和地表背景中进行，如平地、丘陵和树林、草地等等，同时，进一步处理回波数据，提取和分析低熵值强散射点的极化信息，对应其形状和结构，以进一步地对目标进行分类和识别.

［1］范立生，高明星，杨 健，等.极化SAR遥感中森林特征的提取［J］.电波科学学报，2005，20（5）：553-556.FAN Lisheng，GAO Mingxing，YANG Jian，et al.Feature extraction of forested area based on polarimetric SAR［J］.Chinese Journal of Radio Science，2005，20（5）：553-556.（in Chinese）

［2］FENG Xu，JIN Yaqiu.Deorientation theory of polarimetric scattering targets and application to terrain surface classification［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43（10）：2351-2364.

［3］SCHNEIDE R Z，PAPATHANASSIOU K P，HAJNSEK I，et al.Polarimetric and interferometric characterization of coherent scatters in urban areas［J］.IEEE Transactions on Geoscience and Remote Sensing，2006，44（4）：971-984.

［4］CLOUDE S R，GOODENOUGH D G，CHEN H.Compact decomposition theory［J］.Geoscience and Remote Sensing Letters，2012，9（1）：28-32.

［5］GUO R，LIU Y B，WU Y H，et al.Applying H/αdecomposition to compact polarimetric SAR［J］.IET Radar，Sonar ＆ Navigation，2012，6（2）：61-70.

［6］WEHNER D R.High Resolution Radar［M］.Boston：Artech House，1995.

［7］毛二可，龙 腾，韩月秋.频率步进雷达数字信号处理［J］.航空学报，2001，22（增刊）：19-25.MAO Erke，LONG Teng，HAN Yueqiu.Digital signal processing of stepped frequency radar［J］.Acta Aeronautica ET Astronautica Sinica，2001，22（Sup）：19-25.（in Chinese）

［8］BOERNER W M.Basics of SAR Polarimetry I［C］//Rader Polarimetry and Interferomety，Washington DC，2004.

［9］KROGAGER E.A new decomposition of radar target scattering matrix［J］.Electronic Letters，1990，26（18）：1525-1526.

［10］CAMERON W L，LEUNG L K.Feature motivated polarization scattering matrix decomposition［C］//IEEE International Radar Conference.Arlington，May 7-10，1990：549-557.

［11］CLOUDE S R，POTTIER E.A entropy based classification scheme for land application of polarimetric SAR［J］.IEEE Trans on GPS，1997，35（1）：68-78.

［12］FREEMAN A，DURDEN S T.A Three Component scattering model for polarimetric sar data［J］.IEEE Trans on GPS，1998，36（3）：963-973.

［13］郭 雷.宽带雷达目标极化特征提取与核方法识别研究［D］.长沙：国防科技大学，2009.GUO Lei.Reserch on Wide Band Radar Target Polarimetric Feature Extraction and Kernel Method Recognition［D］.Changsha：National University of Defense Technology，2009.（in Chinese）