家兔死后心血氧化还原电位值变化与死亡时间的关系

杨天潼，于永光，白敬，张海东，孙婷怡，Mary G.Ripple，David R.Fowler，李玲，，

（1.中国政法大学教育部证据科学重点实验室，北京 100040；2.北京交通大学理学院，北京 100044；3.华中科技大学同济医学院法医学系，湖北武汉 430030；4.马里兰州法医局，美国马里兰州巴尔的摩 21223）

·论著·

家兔死后心血氧化还原电位值变化与死亡时间的关系

杨天潼1，于永光2，白敬2，张海东1，孙婷怡3，Mary G.Ripple4，David R.Fowler4，李玲1，3，4

（1.中国政法大学教育部证据科学重点实验室，北京 100040；2.北京交通大学理学院，北京 100044；3.华中科技大学同济医学院法医学系，湖北武汉 430030；4.马里兰州法医局，美国马里兰州巴尔的摩 21223）

目的研究在不同温度条件下家兔死后心血氧化还原电位（oxidation reduction potential，ORP）值变化与死亡时间（postmortem interval，PMI）的关系。方法随机将48只家兔分为6组，以空气栓塞法处死后，取家兔右心室血液分别置于10、15、20、25、30和35℃温度下的水浴中，自取血即刻（0h）至死后132h内，每4h用PB-21型电化学分析仪测定样本的ORP值。应用SPSS 17.0软件建立曲线回归方程，再应用MATLAB 7.10.0软件建立曲面方程和三维曲面图。结果不同温度条件下家兔心血ORP值变化与PMI具有高度相关性，温度高时，ORP值上升明显，温度低时，ORP值上升缓慢，并获得拟合的曲面方程以及三维曲面图。结论拟合的ORP值与PMI的曲面方程及三维曲面图可进行温度变化条件下的PMI推断。

法医病理学；死亡时间；氧化还原电位；差值函数；兔

死亡时间（postmortem interval，PMI）推断是法医病理学实践和科学研究中的重大难题，学者们在研究PMI推断的同时，也在不断探讨影响PMI推断的因素，如尸体所处的环境温度、周围土壤的酸碱状态、尸体的腐败程度，甚至环境氧气压力等[1-4]。在这些影响因素中，多数学者认为尸体所处的环境温度是影响PMI推断的主要因素[5-6]。本研究针对环境温度影响PMI推断的问题，应用差值函数（interpolation function）拟合的数学方法，研究不同温度条件下家兔死后心血氧化还原电位（oxidation reduction potential，ORP）的变化规律，建立ORP值与PMI的曲面方程以及三维曲面图，探讨在环境温度变化条件下推断PMI的可行性。

1 材料与方法

1.1 实验动物及分组

家兔48只，雌雄不限，体质量（3000±20）g，由北京市实验动物研究中心提供。家兔被随机分成6组，每组8只。

1.2 主要仪器

PB-21型电化学分析仪［赛多利斯科学仪器（北京）有限公司］。ORP值测量范围：-1500.0～1800.0mV；ORP分辨率：±0.1mV；ORP精度：±0.2mV；温度范围：-5～105℃；温度分辨率：±0.1℃；温度精度：±0.2℃。

SDC-6型低温恒温槽（南京新辰生物科技有限公司）。温度范围：-5～100℃；控温精度：±0.05℃。

1.3 方法

家兔耳缘静脉注射空气栓塞处死，死亡即刻取右心室血液5mL至无菌试管中。将6组家兔血液样本分别放置于10、15、20、25、30和35℃恒温水浴槽中保存待检。取血即刻（0h）至死后132h，每4h取出试管，漩涡振荡10s，消除血液静止后自然沉淀分层的影响。将PB-21型电化学分析仪电极浸入血液中，检测ORP值。

1.4 数据处理与图像分析

应用SPSS 17.0统计学软件进行数据分析及建立曲线回归方程，实验数据用±s表示，用t检验作差异性分析。检验水准α=0.05。

应用MATLAB 7.10.0（R2010a）数学软件（美国MathWorks公司）进行差值分析、曲面方程拟合以及三维曲面图制作。

2 结果

2.1 ORP值检测结果

10、15、20 、25、30和35℃温度下，在取血即刻（0h）至死后132h家兔右心室血液ORP值见表1。

表1 家兔死后不同温度下血液ORP值（n=8，±s，mV）

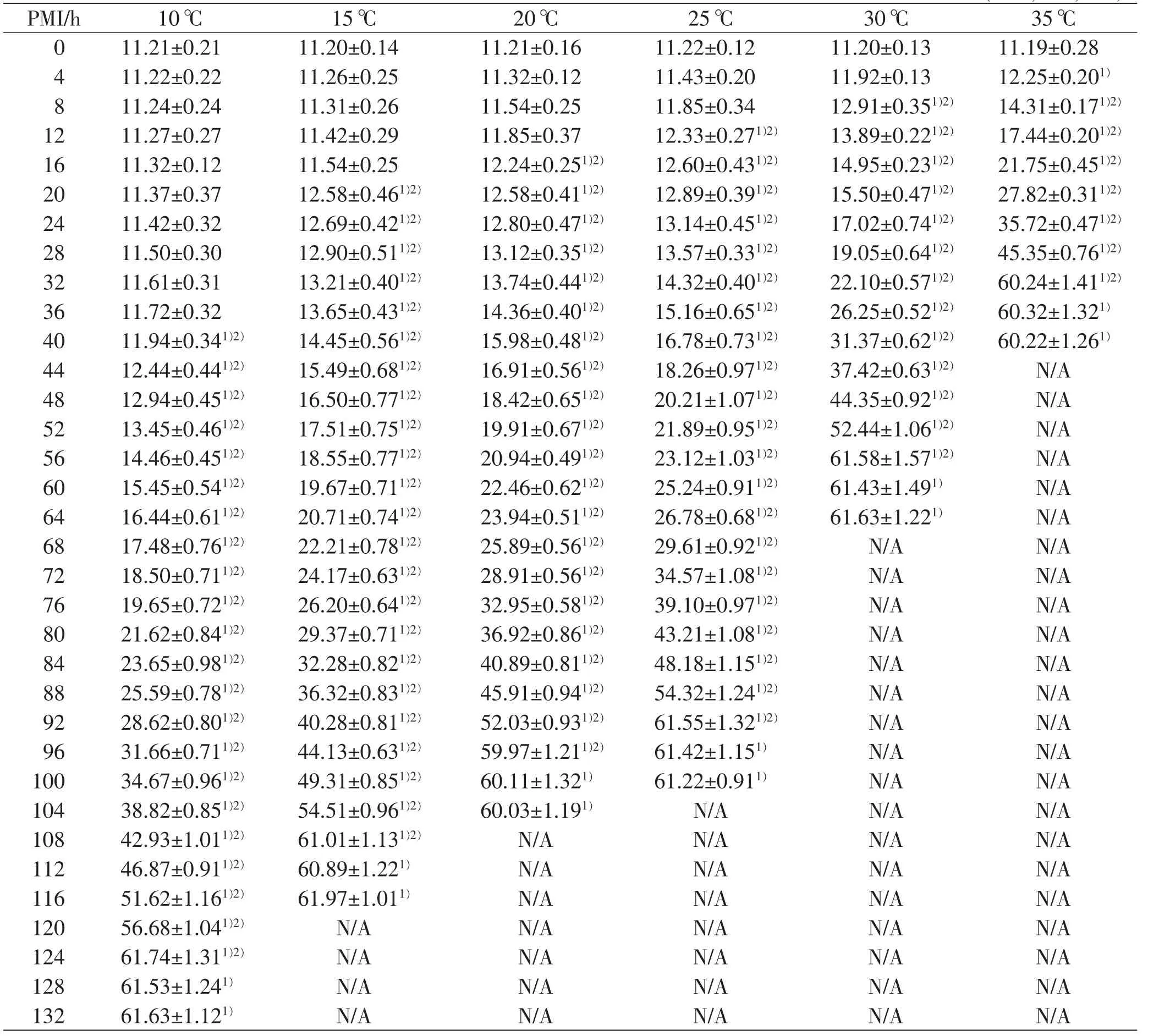
表1 家兔死后不同温度下血液ORP值（n=8，±s，mV）

注：1）与0h比较，P＜0.05；2）与相邻上一时间点比较，P＜0.05；“N/A”表示无统计学意义，因为ORP已无上升趋势，故未检测

PMI/h 10℃15℃20℃25℃30℃35℃011.21±0.2111.20±0.1411.21±0.1611.22±0.1211.20±0.1311.19±0.28 411.22±0.2211.26±0.2511.32±0.1211.43±0.2011.92±0.1312.25±0.201）811.24±0.2411.31±0.2611.54±0.2511.85±0.3412.91±0.351）2）14.31±0.171）2）1211.27±0.2711.42±0.2911.85±0.3712.33±0.271）2）13.89±0.221）2）17.44±0.201）2）1611.32±0.1211.54±0.2512.24±0.251）2）12.60±0.431）2）14.95±0.231）2）21.75±0.451）2）2011.37±0.3712.58±0.461）2）12.58±0.411）2）12.89±0.391）2）15.50±0.471）2）27.82±0.311）2）2411.42±0.3212.69±0.421）2）12.80±0.471）2）13.14±0.451）2）17.02±0.741）2）35.72±0.471）2）2811.50±0.3012.90±0.511）2）13.12±0.351）2）13.57±0.331）2）19.05±0.641）2）45.35±0.761）2）3211.61±0.3113.21±0.401）2）13.74±0.441）2）14.32±0.401）2）22.10±0.571）2）60.24±1.411）2）3611.72±0.3213.65±0.431）2）14.36±0.401）2）15.16±0.651）2）26.25±0.521）2）60.32±1.321）4011.94±0.341）2）14.45±0.561）2）15.98±0.481）2）16.78±0.731）2）31.37±0.621）2）60.22±1.261）4412.44±0.441）2）15.49±0.681）2）16.91±0.561）2）18.26±0.971）2）37.42±0.631）2）N/A 4812.94±0.451）2）16.50±0.771）2）18.42±0.651）2）20.21±1.071）2）44.35±0.921）2）N/A 5213.45±0.461）2）17.51±0.751）2）19.91±0.671）2）21.89±0.951）2）52.44±1.061）2）N/A 5614.46±0.451）2）18.55±0.771）2）20.94±0.491）2）23.12±1.031）2）61.58±1.571）2）N/A 6015.45±0.541）2）19.67±0.711）2）22.46±0.621）2）25.24±0.911）2）61.43±1.491）N/A 6416.44±0.611）2）20.71±0.741）2）23.94±0.511）2）26.78±0.681）2）61.63±1.221）N/A 6817.48±0.761）2）22.21±0.781）2）25.89±0.561）2）29.61±0.921）2）N/AN/A 7218.50±0.711）2）24.17±0.631）2）28.91±0.561）2）34.57±1.081）2）N/AN/A 7619.65±0.721）2）26.20±0.641）2）32.95±0.581）2）39.10±0.971）2）N/AN/A 8021.62±0.841）2）29.37±0.711）2）36.92±0.861）2）43.21±1.081）2）N/AN/A 8423.65±0.981）2）32.28±0.821）2）40.89±0.811）2）48.18±1.151）2）N/AN/A 8825.59±0.781）2）36.32±0.831）2）45.91±0.941）2）54.32±1.241）2）N/AN/A 9228.62±0.801）2）40.28±0.811）2）52.03±0.931）2）61.55±1.321）2）N/AN/A 9631.66±0.711）2）44.13±0.631）2）59.97±1.211）2）61.42±1.151）N/AN/A 10034.67±0.961）2）49.31±0.851）2）60.11±1.321）61.22±0.911）N/AN/A 10438.82±0.851）2）54.51±0.961）2）60.03±1.191）N/AN/AN/A 10842.93±1.011）2）61.01±1.131）2）N/AN/AN/AN/A 11246.87±0.911）2）60.89±1.221）N/AN/AN/AN/A 11651.62±1.161）2）61.97±1.011）N/AN/AN/AN/A 12056.68±1.041）2）N/AN/AN/AN/AN/A 12461.74±1.311）2）N/AN/AN/AN/AN/A 12861.53±1.241）N/AN/AN/AN/AN/A 13261.63±1.121）N/AN/AN/AN/AN/A

2.2 PMI推断的曲线回归方程、曲线图结果

应用SPSS 17.0软件进行数据分析，在10℃条件下，124 h后，ORP值与相邻上一时间点比较，差异无统计学意义（P＞0.05）；在35℃条件下，32h后ORP值与相邻上一时间点比较，差异无统计学意义（P＞0.05）。

本研究以PMI为自变量（x），家兔血液ORP值为因变量（y），得到10、15、20、25、30和35℃温度下家兔血液ORP值与PMI曲线回归方程和曲线图，不同温度条件下的曲线各不相同，温度高时，ORP值上升趋势明显，温度低时，ORP值上升趋势缓慢（表2，图1）。

表2 家兔血液ORP值与PMI曲线回归方程

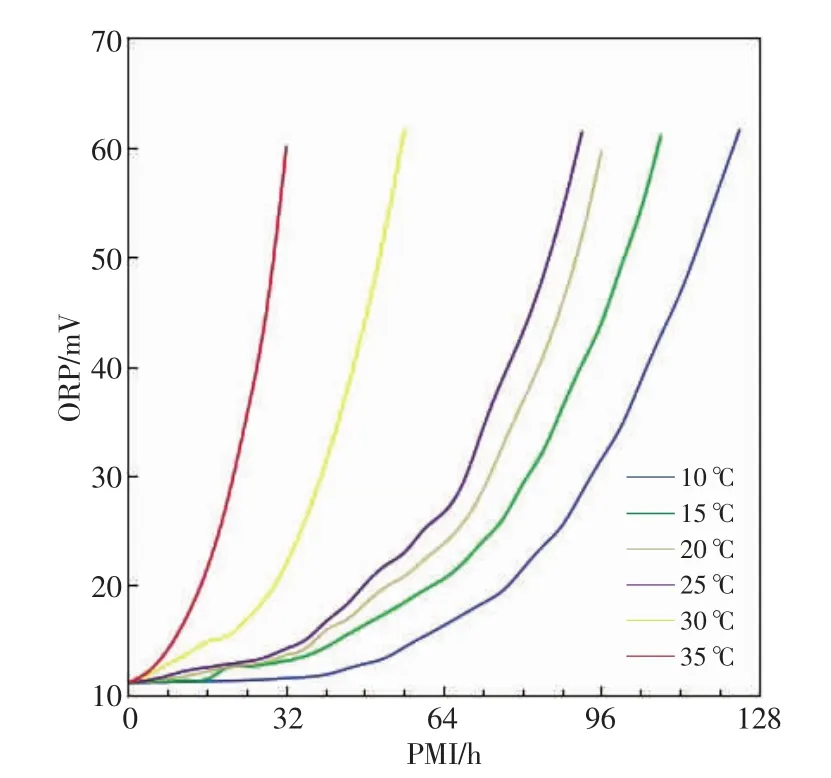
图1 家兔血液ORP值与PMI曲线图

2.3 PMI推断的曲面方程、三维曲面图结果

应用MATLAB 7.10.0软件对上述曲线回归方程进行差值函数拟合，得到以PMI为自变量（x），温度为自变量（y），ORP值为因变量（z）的拟合曲面方程：z=（-7.733 E-7y5+4.340 E-5y4-3.507 E-4y3-1.031 E-2y2+ 8.395 E-2y+11.214）+（-9.440 E-7y5+1.093 E-4y4-4.753 E-3y3+9.615 E-2y2-8.872 E-1y+3.061）x+ （6.667 E-8y5-7.400 E-6y4+3.150 E-4y3-6.375 E-3y2+ 6.068 E-2y-2.190 E-1）x2+（3.455 E-9y5-3.484 E-7y4+ 1.356E-5y3-2.541E-4y2+2.292E-3y-7.891E-3）x3。

对曲面方程进行图像拟合，得到三维曲面图（图2）。

图2 家兔血液ORP值与PMI三维曲面图（灯光效果）

3 讨论

为了解决外界环境温度影响PMI推断的法医学问题，一直没有一种既准确又客观的方法应用于鉴定实践中。多数学者认为，由于尸体处于不断变化的环境温度中，因此，单一温度下、单一物质的死后变化规律已经不适合用来进行准确的PMI推断[7-8]。最近研究表明，数学方法越来越多应用于解决环境温度影响PMI推断问题，如广义相加模型（generalized additive models）或支持向量机法（support vector machines）等[9-10]，但依然没有一种可广泛应用的方法。本研究对10、15、20、25、30和35℃温度下家兔右心室血液的ORP值进行检测，发现在不同温度条件下，ORP值与PMI曲线回归方程各不相同。曲线图显示，当温度低时，ORP值变化趋势缓慢，温度高时，ORP值变化趋势明显，不同温度条件下的曲线图各不相同。本研究结果说明，单一温度下，某种物质的死后变化规律只能反映该温度下的PMI，而不能用作不同温度条件下的PMI推断。而法医学实践中面临的实际情况需要推断处于外界环境温度不断变化条件下的PMI，显然单一温度条件下的物质变化规律只能大致反映实际情况下的PMI分布，而不能用于进行准确的PMI推断，这也是法医学PMI推断研究一直未获突破的原因[11-12]。

本研究将处于外界环境温度变化的PMI推断过程进行分解，将这种连续变化的温度变化趋势人为减缓或暂停于某一个温度点上，之后再将其整合起来进行PMI推断，即在某一固定温度条件下，所检物质在单一温度条件下降解或改变，之后又在另一温度下发生改变，将不同单一温度条件下的PMI推断方程集合起来，并以统计、数学的方法体现这种集合。这种方程集合体现在统计图上，结果就是形成一定温度区间内，所有单一温度条件下物质随PMI变化的曲线集合而成曲面。这一曲面将包含该温度区间内所有单一温度条件下物质死后变化的曲线，也包括这一温度区间内所有PMI推断的时间点，通过数学拟合的方法，就可以用拟合曲面方程的方式表达这个曲面的变化趋势。差值和拟合都是数据优化的一种方法，是离散函数逼近的重要方法，利用差值函数可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。因此，差值函数可以有效填充图像变换时像素之间的空隙，该方法可用来拟合已知多条曲线方程，从而得到曲面方程，并绘制三维曲面图[13-14]。

本研究中，由于右心室血液具有采样容易、样本量充足、检材处理方法相对简便，可供检测项目广泛等优势，选择家兔右心血液作为研究对象，同时考虑到本研究的目的在于推导PMI推断的曲面方程，尽量简化实验步骤、消除实验的人为误差至关重要，因此选择ORP值为检测指标，其具有操作简便、技术成熟和测量准确等优势，可用来反映溶液中所有物质表现出来的宏观氧化还原性。对于大多数生物学体系来说，氧化还原电位是多种氧化物与还原物质发生氧化还原反应的综合结果，是一项综合性指标。血液中含有大量的离子和有机物质，当机体死亡后，血液中的离子和有机物质发生死后变化，导致ORP值也发生改变，如果血液中的ORP值的改变有时间规律性，则可以应用于PMI推断[15]。本研究结果表明，在所检温度点内，ORP值与PMI均呈良好的线性关系，其R2在0.974～0.986，说明ORP值可以很好地反映单一温度条件下的PMI变化，因而可以用ORP值与PMI的曲线回归方程推导曲面方程。另外，本研究尽可能对实验温度进行了控制，所采用的PB-21型电化学分析仪的温度分辨率为±0.1℃，温度精度为±0.2℃，控制标本死后变化温度的低温恒温槽控温精度为±0.05℃，可以反映单一温度条件下ORP值的变化规律，从而保证曲面方程的拟合精度。本研究应用MATLAB 7.10.0数学软件进行曲面方程拟合，是一种高级的矩阵（阵列）语言，可进行矩阵运算、线性方程组及差值函数拟合等运算，同时具有求解二维曲线和三维曲面的绘制和处理等功能，保证了曲面方程的拟合精度[16-17]。

本研究所得到的曲面方程由温度、ORP值和PMI得出，曲面上每一个点的坐标由温度、ORP值和PMI确定，该曲面包括在这一段温度区间内所有PMI点，因此只要获得了温度和ORP值，就可以得到温度变化条件下的PMI。需要指出的是，该曲面方程由多条单一温度条件下得曲线拟合而成，理论上，应用该公式可以获得无限长的PMI，随着血液中的离子和有机物质死后变化的终止，ORP值也必然稳定在某一区间，而不会持续升高。因此，该公式在实践应用时有一定限制。本研究结果显示，在10℃条件下，可供检测的PMI窗口为0～124 h，但在35℃条件下，可供检测的时间PMI窗口仅为0～32h。在今后的研究中，可以通过进一步选择死后变化缓慢的物质，来扩展PMI推断的时间窗口，也可以检测更多单一温度条件下的物质死后变化规律，增加拟合曲线数量，从而提高三维曲线方程拟合精度。另外，由于本研究的目的在探讨外界环境温度变化条件下，利用曲面方程推断PMI的可行性，研究的关键在于精确控制实验温度，从而获得单一温度条件下精确ORP值的变化规律，因此只能选择离体血液检测方式，这虽然与实际情况有所不同，但初步得到了多种温度条件下、较为精确的ORP值随PMI的变化曲线回归方程，并以此为基础，推导出了推断PMI的曲面方程和三维曲面图，已经达到了实验目的。

因此，本研究仅对外界环境温度变化条件下的PMI推断进行了初步探讨，仍需后期实验、尤其是人体实验证实。总之，本研究将以往在二维空间内应用曲线回归方程推断PMI，拓展至三维空间内应用曲面方程推断PMI，为法医学PMI推断提供新的研究思路。

（本研究得到中国政法大学青年教师学术创新团队资助项目资助。）

[1]Vass AA. The elusive universal post-mortem interval formula[J]. Forensic Sci Int，2011，204（1-3）：34-40.

[2]Forbes SL，Stuart BH，Dadour IR，et al. A preliminary investigation of the stages of adipocere formation[J]. J Forensic Sci，2004，49（3）：566-574.

[3]Forbes SL，Stuart BH，Dent BB.The effect of the burial environment on adipocere formation[J]. Forensic Sci Int，2005，154（1）：24-34.

[4]Megyesi MS，Nawrocki SP，Haskell NH.Using accumulated degree-days to estimate the postmortem interval from decomposed human remains[J].J Forensic Sci，2005，50（3）：618-626.

[5]Ith M，Scheurer E，Kreis R，et al. Estimation of the postmortem interval by means of1H MRS of decomposing brain tissue：influence of ambient temperature[J]. NMR Biomed，2011，24（7）：791-798.

[6]Poloz YO，O’Day DH.Determining time of death：temperature-dependent postmortem changes in calcineurin A，MARCKS，CaMKⅡ，and protein phosphatase 2A in mouse[J]. Int J Legal Med，2009，123（4）：305-314.

[7]Kimura A，Ishida Y，Hayashi T，et al. Estimating time of death based on the biological clock[J]. Int J Legal Med，2011，125（3）：385-391.

[8]Matoba K，Terazawa K.Estimation of the time of death of decomposed or skeletonized bodies found outdoors in cold season in Sapporo city，located in the northern district of Japan[J]. Leg Med（Tokyo），2008，10（2）：78-82.

[9]Muñoz Barús JI，Febrero-Bande M，Cadarso-Suárez C. Flexible regression models for estimating postmortem interval（PMI）in forensic medicine[J].Stat Med，2008，27（24）：5026-5038.

[10]Roca-Pardiñas J，Cadarso-Suárez C，Nácher V，et al. Bootstrap-based methods for testing factor-by-curve interactions in generalized additive models：assessing prefrontal cortex neural activity related to decision-making[J]. Stat Med，2006，25（14）：2483-2501.

[11]Karargyris A，Bourbakis N.Three-dimensional reconstruction of the digestive wall in capsule endoscopy videos using elastic video interpolation[J]. IEEE Trans Med Imaging，2011，30（4）：957-971.

[12]Guetat A，Ancel A，Marchesin S，et al. Pre-integrated volume rendering with non-linear gradient interpolation[J]. IEEE Trans Vis Comput Graph，2010，16（6）：1487-1494.

[13]李莉，屈桢深，曾庆双.扩展差值函数及其在图像运动估计中的应用[J].吉林大学学报（工学版），2008，38（4）：897-901.

[14]郑小龙，叶红玲，隋允康，等.最大差值极小化的响应面函数拟合方法[J].科技导报，2010，28（17）：36-41.

[15]Mannery YO，Ziegler TR，Park Y，et al. Oxidation of plasma cysteine/cystine and GSH/GSSG redox potentials by acetaminophen and sulfur amino acid insufficiency in humans[J]. J Pharmacol Exp Ther，2010，333（3）：939-947.

[16]Markiewicz T. Using MATLAB software with Tomcat server and Java platform for remote image analysis in pathology[J]. Diagn Pathol，2011，6（S1）：S18.

[17]吕品品.浅谈MATLAB 在数字图像处理中的应用[J].数学技术与应用，2010，（9）：152.

（本文编辑：刘宁国）

Correlation between the Changes of Oxidation Reduction Potential Values and Postmortem Interval of Heart Blood in Rabbits after Death

YANG Tian-tong1,YU Yong-guang2,BAI Jing2,ZHANG Hai-dong1,SUN Ting-yi3,Mary G.Ripple4, David R.Fowler4,LI Ling1,3,4
（1.China University of Political Science and Law,Key Laboratory of Evidence Science,Ministry of Education, Beijing 100040,China;2.School of Science,Beijing Jiaotong University,Beijing 100044,China;3.Faculty of Forensic Medicine,Tongji Medical College,Huazhong University of Science and Technology,Wuhan 430030, China;4.Office of the Chief Medical Examiner of Maryland,Baltimore 21223,USA）

ObjectiveTo investigate correlation between the changes of oxidation reduction potential（ORP）values of heart blood in rabbits after death and postmortem interval（PMI）at different temperatures.MethodsForty-eight rabbits were randomly divided into 6 groups and sacrificed by air embolism.Blood samples were taken from the right ventricle of each rabbit and stored at different temperatures of 10,15,20, 25,30 and 35℃,respectively.Every 4 hours from 0h to 132h postmortem,the ORP values of the blood samples were measured at different intervals by PB-21 electrochemical analyzer.The curvilinear regression equation was established by SPSS 17.0 software.The surface equation and 3D surface diagram were established by MATLAB 7.10.0 software.ResultsThe ORP values at different temperatures of heart blood in rabbits were highly correlated with the PMI.The ORP values rised obviously when the temperature was high and rised slowly when the temperature was low.The surface equation and 3D surface diagram were obtained.ConclusionThe surface equation and 3D surface diagram of ORP values and PMI may be used for PMI estimation at different temperatures.

forensic pathology;postmortem interval;oxidation reduction potential;interpolation function; rabbits

DF795.1

A

10.3969/j.issn.1004-5619.2013.05.001

1004-5619（2013）05-0321-04

国家自然科学基金青年科学基金资助项目（81001349）；教育部长江学者和创新团队发展计划项目（IRT0956）

杨天潼（1977—），男，吉林长春人，博士，讲师，主要从事法医病理学、法医临床学研究；E-mail：yangtiantong@126.com

李玲，女，教授，主要从事法医病理学研究；E-mail：ling001@aol.com

2011-12-29）