融入能力互补因素的生产联盟伙伴选择研究*

琚春华 ，傅小康

（1.浙江工商大学计算机信息与工程学院 杭州 310018；2.浙江工商大学现代商贸中心 杭州 310018；3.浙江工商大学管理学院 杭州 310018）

融入能力互补因素的生产联盟伙伴选择研究*

琚春华1，2，傅小康3

（1.浙江工商大学计算机信息与工程学院 杭州 310018；2.浙江工商大学现代商贸中心 杭州 310018；3.浙江工商大学管理学院 杭州 310018）

资源的互补整合是企业联盟的主要目标，互补度的高低是决定企业联盟稳定性及联盟绩效的关键因素，本文针对生产联盟伙伴选择问题，提出了基于能力互补的选择策略，定义并深入剖析了基于生产能力的互补度评价系数。并在此基础上，构建了融入互补度评价系数的生产联盟伙伴选择3阶段模型，模型首先采用层次分析法和基于粒子群优化算法的多目标搜索算法，求得生产时间和生产成本的双目标帕累托最优解，再通过评价非劣解的互补度补充指导决策，最后选择通信行业的智能手机制造联盟中的伙伴选择问题作为仿真应用，分析了仿真结果并给出了结论。

伙伴选择；互补度；粒子群优化算法；帕累托最优解

1 引言

动态联盟是指通过与厂商、顾客、甚至同行竞争对手形成联盟，整合内外资源，在快速变化的市场环境下达到协同共赢（win-win）的目的。关于动态联盟的研究主要集中在伙伴选择、协同运作、风险规避、利益分配等问题上，其中伙伴选择（partner selection）是建立联盟的开始，亦是影响联盟绩效的关键[1]。虽然在伙伴选择模型及求解算法上已有较多的理论成果，但由于信息的不确定性、期望目标的复杂性和情境的多样性，伙伴选择的研究依然富有挑战性。

目前关于动态联盟伙伴选择目标主要有成本最低、质量最佳、生产周期最短、客户满意度最高、风险性最小等[2～10]特点，用互补度作为选择指标的尚且不多。由于决策标准不仅涉及价格、时间等短期目标因素，更涉及信任、处事风格、合作规则等历史合作因素，因此，研究联盟稳定性对我国的“关系”文化背景下的合作伙伴选择颇有战略意义。参考文献[1]指出企业倾向与资源互补度高的企业结盟；参考文献[11]也提出互补度高的联盟稳定性更高，即互补度高的企业结盟再次结盟的概率更高。因此，本文提出了基于互补度的联盟伙伴选择方法，首先对候选企业的生产能力进行建模，然后通过智能算法求得帕累托最优解集，最后将互补度作为决策标准进行伙伴选择。

目前，针对多目标选择问题已有较多研究成果，主要有层次分析法（analytic hierarchy process，AHP）[2,3]、网络分析法 (analytic network process，ANP）[4,5]、形式概念分析（formal concept analysis,FCA）法[6]等，然而上述方法对定性的概念分析要求过高，实际应用中有些方面考虑还不够全面。在智能算法运用方面，有运用蚁群算法（ant colony optimization，ACO）[7]、贝叶斯算法（Bayesian algorithm）[8]、多目标遗传算法 （multi-objective genetic algorithm，MOGA）[9]等，然而所得的帕累托最优解并不唯一，尚待进一步决策。此外，针对不确定情境，参考文献[8]将专家系统（expert system，ES）应用于国际合资企业的伙伴选择问题，参考文献[12]在研究中融入了模糊数学（fuzzy mathematics）、随机过程（stochastic process）等方法，参考文献[13]则引入了博弈论（game theory）等管理机制 。

虽然伙伴之间互补的重要性曾多次被学者述及，也存在一部分的实证研究，但是关于企业与所选合作伙伴之间互补度的研究依然较少，其中关于定量互补度的研究则更为不足。参考文献[11]的研究表明，选择企业联盟伙伴时，倾向于具备互补性资源的企业，指出建立联盟时要尽可能吸收技术能力互补的企业，以尽可能地整合联盟内部力量；同时提出建立入盟激励约束模型时，定义了入盟企业的技术能力与联盟技术能力的互补参数，但未对此互补参数的定义做出具体解释。参考文献[14]在研究联盟稳定性时，定义了互补因子，但该因子无法用于合作伙伴必须参与的任务模型。参考文献[15]运用匹配理论对IT人员的业务能力和技术能力的互补性做了研究，指出当两种能力均达到一定的水平时，可产生协同效应，从而提升经营绩效。

针对上述伙伴选择的参考文献中互补度研究的不足，本文在Cao Qing、Wang Qiong等建立的经典企业合作伙伴选择模型[2]的基础上，建立了融入能力互补因素的企业生产联盟的3阶段伙伴选择模型。该模型针对生产能力特性，定义了互补度评价系数，在模型的第3阶段将互补度作为选择参考，旨在动态合作伙伴选择时，解决既考虑成本、时间等短期动态目标，又考虑联盟稳定性这一战略目标的伙伴选择问题。

2 基于生产联盟伙伴组合互补度的分析及定义

2.1 生产联盟企业间互补的作用

互补的意义因设计、制造、销售、服务等职能的不同而发生变化，本文主要分析基于生产制造的互补。由于产品的生产制造有复杂的过程，涵盖不同的工艺，需要多样的设备，但一些设备造价昂贵，中小企业可能无法拥有全套设备，因此，不同企业拥有不同的生产能力或擅长不同的生产方向。企业关注核心能力的提升，可以只完成部分订单的生产任务，将其他生产环节交由联盟合作伙伴协同完成。企业联盟的形成必将产生协同成本，包括物流费、中介合同费、联盟的协调运作费等。一般而言，联盟企业之间的互补性越强，其协同成本越低[11]。因此，为提高整个联盟体的效益，须选择互补度高的企业，使联盟体的各种能力、资源、市场等因素平衡发展。

基于生产能力的互补，指的是通过与一个或多个企业建立联盟，从不同企业中获取所需要的能力，突破企业能力缺陷障碍，使联盟整体的企业能力体系中各项能力达到均衡并得以充分发挥。理想的战略性生产联盟的生产能力互补，可以完成行业内通用产品的生产，并且能力盈余最低。生产联盟中倘若有的能力过剩，而有的能力却不佳或缺失，那么这种联盟就不是满意的联盟。具体如图1所示，图1（a）中，交集面积之和决定互补系数的高低，面积越大，互补系数β越大，图1（b）为互补系数β=100时的最佳互补。

图1 基于生产能力的互补定义

基于生产联盟的特性，本文将互补分为横向互补和纵向互补，最佳纵向互补为在生产成本、时间、质量等约束条件下寻求多目标最优，并且联盟整体的生产能力剩余率最低。最佳横向互补则为各个联盟企业所产生的协同环境最佳。

2.2 基于生产能力的纵向互补度的计算方法

首先定义模型中的各种符号，具体定义如下。

·E0：主选（盟主）企业。

·Ei：第 i家备择企业（i>0）。

·E=[E1，E2，…，Ei]：备择企业集。

·T：外包能力需求集。

·Tj：第 j项任务。

·Tpq：第p项任务选择第q家企业作为合作伙伴。

·cij：第i家企业完成任务j所需要的单位成本。

·tij：第i家企业完成任务j所需要的单位时间。

·LT：提前期（lead time）。

·TC：生产总成本。

·TT：生产总时间。

·NUM：伙伴数目。

·{S1，S2，S3，…，Sn}：帕累托最优解集。

·βSi：解Si的伙伴组合互补度评价系数。

·Β={βS1，βS2，βS3，…，βSn}：纵向互补度评价集。

·j’：第j项任务的前道（工序）任务。

·i’：完成当前任务的前道工序的企业。

·ccii’：第i′家企业到第i家企业之间的协同成本，如果没有前道工序，则 ccii′=0。

如图2所示，若一个生产链的生产能力需求为{A，B，C，D，E，F，G，H}，则假设甲生产能力为{A，B，C，D，E}，乙为{F，G，H}，丙为{A，B，F，G，H}。假设企业甲乙联盟和企业甲丙联盟产生的成本、时间、质量等相当，就同等条件下的再次联盟概率而言，甲乙再次联盟的概率肯定比甲丙高，因为甲乙两家企业的互补度高，而甲丙联盟必然会造成一方的生产能力A和B不起作用，造成资源空置。

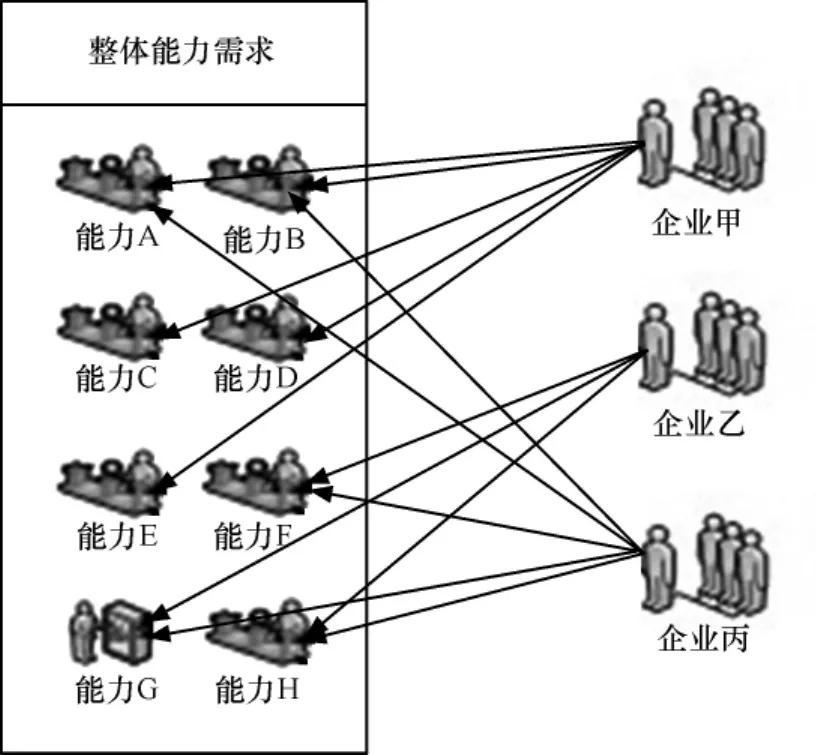
图2 盟友企业能力组合

互补度系数是体现企业资源的互补程度的量化指标，与不同联盟中伙伴之间的共性能力数量成反比。假设某生产链共需M种能力，记为T，为了体现能力高低不等，将每个能力属性分3个等级，如能力A分为3个级别：A+，A，A-。

假设主选能力集为T的子集，记T-E0=[]，第i个候选企业记为Ei，候选企业能力为子集记为T-Ei=[]，将第j种单项能力重叠度的Δm定义为（以能力A为例）：

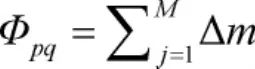
标准化后的β取值范围为(0,100］。互补度等级是由共性资源的数量决定的，等级越高，互补度越低。如图3所示，联盟组合的互补度β根据生产能力剩余的数量分为不同的等级，将相同互补度等级的联盟组合视为互补度相当解，对互补度相当的解需进一步考察联盟的横向互补度，进而产生最优解。

2.3 企业联盟中横向互补度的衡量标准

协同效应是由联盟企业的合作氛围、协作文化以及联盟的治理结构的效率等联盟环境所决定的[13]。为了使联盟的生产能力、营销能力、财务能力、研发能力、人力资源能力拥有最佳的发展环境[10]，企业必须追求高度的横向互补才能达到协同效应。

横向互补度的具体衡量标准主要包括以下3方面。

（1）管理相容性

具备相容的管理风格、相容的战略目标，制造商和经销商之间有相同或者更高的技术能力水平、以往的联盟经验、伙伴的管理能力。

（2）营销互补度

更宽的市场覆盖范围，拥有增长的市场份额，更多的出口机会，拥有不同的客户、不同的营销手段。

（3）文化协同度

是否愿意共享专有技术、平等控制、灵活性。协同的文化，相似的文化，相容的文化，冲突的文化。协同度高，对绩效产生正向影响。

以企业能力为基础建立能力管理框架，本文从纵向和横向两方面评价企业之间的互补性，首先从定量的角度考察具体生产任务完成能力的纵向互补度，其次定性地评价联盟组合的横向互补度，包括企业的营销能力互补、管理能力互补、文化适应能力互补。如果综合互补度高，则易于形成战略合作伙伴。

3 基于生产的动态联盟伙伴选择模型的建立

基于生产的动态联盟，对生产能力的需求明确，易于评估联盟伙伴的互补度。盟主企业接到订单后，首先必须评估自己的生产能力和生产负荷；然后进行需求分析并在行业内发布需要外包的生产能力需求；最后各个想要入盟的企业通过分析自身能力，响应需求并出样报价。本文构建了基于生产的3阶段选择模型，如图4所示，旨在解决在众多备择企业中选择伙伴的难题。

3.1 逻辑模型建立

如图4所示，基于生产的动态联盟伙伴选择包括3个阶段。

图3 互补度系数逐级分布

第1阶段，盟主企业获得一批备择企业的信息，根据其声誉、商标、产品质量、负债等基本信息和历史合作信息，剔除一些不合格企业，产生候选企业集。

第2阶段，依据各生产能力的提供厂商的报样的价位及生产周期，寻求总生产成本最低和生产时间最短的企业，通过基于粒子群优化算法的多目标搜索算法，得到帕累托最优解集。

第3阶段，通过评价非支配最优解的互补度，将纵向、横向互补度融入非劣解中选择的决策规则之中，形成最佳决策。

3.2 数学模型建立

假设第p项任务选择第q家企业作为合作伙伴，即针对Tpq设置基本向量Vpq：

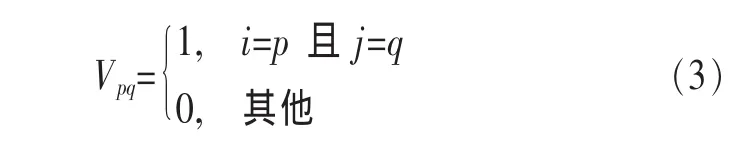
假设使用PRET网络流程图计划排程，对每个Tpq设置另一个基本向量Rpq：

假设企业的能力成本矩阵为C：

其中，有N家联盟内企业（包含盟主企业），总共有M种能力。cij的值为：

式（6）表示的是第i家企业提供的第j能力所产生的单位成本。若第i家企业没有第j中能力，则用0补齐。

同理得出协同生产矩阵TC和生产时间矩阵TT，CC由ccij组成，T由tij组成，得出目标函数如下：

约束条件为 NUM≤3；TT≤LT；i≥0；j∈[0,N]。

4 基于生产的动态联盟伙伴选择寻优算法

针对每一阶段模型特点设计模型求解方法，具体如图5所示。

第1阶段，建立备择企业的基本信息库和联盟历史信息库，运用层次分析法（AHP），对备择企业的历史合作信息、品牌、质量等决策标准的分类，确定权重，专家进行模糊评价，产生候选企业集。

第2阶段，运用基于粒子群优化算法的多目标搜索算法，对生产时间和成本进行优化求解，产生帕累托非劣解集。

第3阶段，通过评价非支配最优解的互补度，将纵向、横向互补度融入非劣解中选择的决策规则之中，形成最佳决策。AHP方法在伙伴选择中已有较多研究，本文不再赘述。下面主要介绍基于粒子群的多目标搜索算法的设计应用和基于互补度评价的决策支持方法。

4.1 基于粒子群优化的多目标搜索算法

多目标求解属NP难题，设外包任务能力5种，共有25家盟友企业，且每种能力有15家备择企业具有。那么，有155种（759375种）选择的可能，计算量非常大，必须依靠智能算法才能得到最优解，粒子群优化算法是计算智能领域除了蚁群算法、鱼群算法之外的又一种群体智能优化算法。具体流程如图6所示。该算法最早是由Kennedy和Eberhart在1995年提出的，主要源于对鸟类捕食行为的研究。算法中的每个粒子都代表问题的一个潜在解，每个粒子对应一个由适应度函数决定的适应度值，粒子的速度决定了粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整。粒子在解空间中运动，通过跟踪个体极值Pbest和群体Gbest更新个体位置。

图5 求解过程

图6 粒子群优化算法流程

假设在D维搜索空间中，由n个粒子组成的种群X=（X1，X2，…，Xn），其中第 i个粒子表示一个 D 维向量 Xi=（xi1，xi2，…，xid）T，代表第 i个粒子在 D维搜索空间中的位置，亦代表一个潜在解。根据目标函数可以计算出每个粒子Xi对应的适应度值。算法主要包括以下6个步骤。

（1）编码

本文采用自然数对初始粒子群进行编码。D维向量空间代表D项外包能力需求，自然序数代表候选企业的编号，设某一粒子 Xi=（xi1，xi2，…，xid）T=[2，5，2，3，5，3，3]T。

（2）解码

个体代表第i1种能力由第xi1家企业提供服务。如（1）中Xi的解码为：第1种生产能力由第2家企业提供；第2种生产能力由第5家企业提供，以此类推。

（3）初始粒子群产生

初始粒子群是半随机产生的，每个任务集均有通过初选的候选企业，在通过初选的候选企业中随机产生个体。

（4）适应度赋值

基于个体的式（6）和式（7）排序的是适应度赋值。利用线性差值方法在最低序号与最高序号之间插入数值，具有相同序号的个体进行适应度共享操作。个体须满足上文中的约束。

（5）筛选非劣解集

当前粒子不受其他粒子以及当前非劣集中粒子支配时，把新的粒子放入非劣解集中；若新的粒子支配当前非劣集中的粒子，则将当前非劣集中的受支配的解剔除。并且在粒子更新前从非劣解集中随机选择一个粒子作为群体最优粒子。

（6）粒子最优更新

其中，w为惯性权重；r1和r2为分布于[0,1]的随机数；k是当前的迭代次数为个体最优粒子位置为全局最优粒子位置；c1，c2为常数；V为粒子速度；X为粒子位置。

通过限定范围内随机产生初始种群，由于是多目标两两比较淘汰劣解，所以种群规模要相对较大（xSize>30）。在粒子种群更新过程中，非劣解集中的支配粒子总量不达种群规模要求的，用随机产生填补。若非劣解个体和通过变异交叉产生的个体总量大于种群规模，则采用扩大子代种群规模策略。

4.2 第3阶段模型求解

运用本文的2.2节中的互补度β计算方法，可产生纵向互补度评价集，记为 Β={βS1，βS2，βS3，…，βSn}，定量能力互补度β排序法求解最佳生产能力互补组合，纵向互补度最大值记为Maxβ。

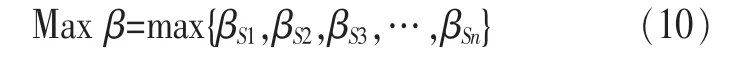
设Maxβ互补度等级为m，若存在其他解的β值等级与最高级相同，则将m等级的β的解视为纵向互补度相当，需进一步定性考察该等级所有解的横向互补度。

针对互补度等级为m的解不唯一的情况，为获得最佳联盟合作环境，定性判断联盟伙伴间的横向互补度。通过对第1节介绍评价营销能力、管理能力、文化适应能力的综合横向互补度，确定最终的决策。

5 我国通信行业智能手机生产联盟伙伴选择实例研究

本文以通信行业智能手机的生产为例，对上述伙伴选择方法进行模拟仿真。智能手机（Smartphone）具有独立的操作系统，可由用户自行安装软件、游戏等程序来不断扩充手机功能，并可通过移动通信网络实现无线网络接入。艾媒咨询（iiMedia research）的数据显示，2012年第3季度我国智能手机市场销量达到4980万部，环比增长31.1%，同比增长154.9%[16]。国外知名智能手机品牌有如美国的苹果（iPhone）、韩国的三星（Samsung）、加拿大的黑莓（Blackberry）等。在国内，某些品牌也奋力占据中、低端的市场，如华为、酷派、联想、小米、金立、天语等。由于手机生产过程的复杂性，即使是美国苹果公司，全球也有218家供应商为其生产零件，故有相当一部分手机集成商组织运作交织复杂的手机生产联盟网络。以深圳华强北地区的手机产业链为例，虽然大部分主板采用台湾联发科技的MTK芯片，但不同的功能方案需要不同的车床组成，并且测试过程复杂，所以存在很多手机生产联盟。

5.1 智能手机主要生产能力分类

如图7所示，智能手机的生产主要由3部分组成：主板部分、配件及外观、整机组装与测试系统。

以某品牌普通智能手机为例，其主要制造流程如图8所示，生产工序有A～M，共包含14道工序，每一道工序代表特定类别的生产能力，生产的关键路线为A-B-C-D-E-I-J-K-N。

5.2 生产联盟伙伴选择模型中的各参数的确定

假设需定制3000个中端智能手机，LT=20天，TC=180万元。设盟主可以独立进行工序A/B/D/E/I/J/L/M/N，其中主板芯片、听筒、麦克风、摄像头、喇叭标准件可在电子市场采购，盟主企业还具备主板功能模块加工、整机装配、软件灌装、测试、说明书撰写、包装等生产能力，除此之外，还有液晶模块等5道生产工序需要外包给盟友伙伴完成。假设根据历史合作信息、企业信息，通过AHP滤除不合格企业后，还剩余20家候选企业愿意加入联盟提供该服务。故 i=1～20，j=1～5，E=[E1，E2，E3，…，E20]。

通过对深圳华强北地区部分智能手机生产企业的实地调查以及网络数据分析，获知每个模块的生产价格区间、生产周期等信息。发现不同企业所提供的完成时间和单位生产价格有所差异，因此，企业之间的协同成本必然也有差异。在协同成本计算上，主要体现在前后道工序的生产厂家的货品运输费、仓储费以及建立联盟的合同费等。在此基础上设计仿真数据，得到生产成本矩阵C、生产时间矩阵TT以及协同成本矩阵CC。检测失败回炉的时间和成本按5%计算。

5.3 应用MATLAB仿真及对仿真结果的分析

5.3.1 仿真过程及仿真结果

图7 智能手机的生产构成

图8 智能手机生产过程

由于粒子群算法的数据分析比较复杂，而MATLAB拥有强大的矩阵运算功能、图形化显示功能，因此选择MATLAB作为程序设计工具。应用本文阐述的基于粒子群的多目标寻优算法，将迭代总数设为1000，种群大小设为50，精度则为待招标的工序数5，最大合作企业数目设为3。具体的实现步骤如下。

（1）运用模型第2阶段求解算法。随机产生的初始种群的平均总生产时间30天、总生产成本为375.7万元，运行求解算法1000代后，平均总生产时间16.5天、总生产价格为171.8万元，结果表明，第2阶段的算法具备较好的收敛性和理想的求解效果。最终得到的帕累托最优解有12 个，按生产时间排序后得到 S=[S1，S2，S3，…，S12]。如图 9所示为逐代的平均目标值的进化过程及图10所示的最终非裂解排序后分布。

（2）根据生产成本约束条件不高于180万，生产周期不多于20天的要求，将解集中的解序号为1、2、3、12的解剔除。

（3）计算纵向互补度评价集，由于已删除 1、2、3、12 号解，故不需再计算其互补度，剩余互补度记为 Β={βS4，βS5，…，βS10}。

标准件A/D/E/L的生产能力在计算互补时不作为能力考虑，剩余通过设计得到仿真能力专家评价子集。核心企业 E0的能力子集 C-Key E=[B-，I，J+，M，N+]，各候选企业的能力子C-Ei。如图11所示，按照从下往上的顺序，第1层代表生产智能手机时，除标准件之外的总的生产能力需求{B，C，F，G，H，I，J，K，L，M，N}；第 2 层为帕累托最优解集中涉及企业的能力评价子集；经粒子群算法求解得到中间层——帕累托解各方案的能力评价组合，如E0∪E3；最上层为每个帕累托最优解方案的纵向能力互补度β值的计算结果。根据上文定义得出B=[14.1831.2524.3913.723.8116.3916.6719.42]，剩余可行解中互补度最高的解序号 S5：{E0，E5}，其互补度为 31.25，互补度等级为 3。由于最高互补度级别解仅有一个，故选择结束。选择结果：S4为最佳伙伴选择策略。

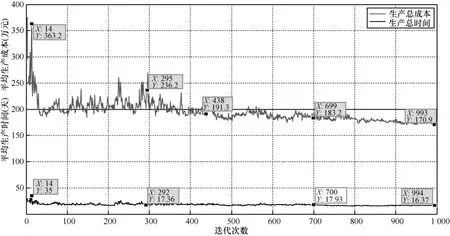
图9 逐代目标值均值曲线

图10 运行1000代以后帕累托解分布

图11 互补度计算概念

（4）若步骤（3）中最高互补度级别不止一个，则需要进一步结合企业间的横向互补度的高低，继续选择。

本文所用的仿真在步骤（3）结束。

5.3.2 仿真结果分析

（1）算法得到的帕累托解集在进行排序之后，较之其他解，两端的非劣解特点为其中一个目标最优，而另一个目标则最劣。如：曲线最左端的解是生产时间最短为12天，而生产成本为解集最高，为192.6万元，平均每台智能手机的生产价格为640元。

（2）在S1～S12解曲线的中间段，目标值的变化幅度并不大，如 S5～S9，时间为 16～18天，生产成本则为：175.7～166.5万元，每台成本555～585元。运用模型的第3阶段继续辅助支持决策者，不再继续求解互补度的选择方法只能盲目从中选择。即通过图11的最高一层，解决了上述双目标差异不大造成的决策困难。此过程可进一步根据考虑决策者的决策偏好，如成本优先战略等先缩小β值的求解范围。

（3）在本文案例中，Maxβ的互补度级别为3，而且仅有一个β值居第3级，选择结果非常清晰。倘若在图11最高层，若存在于Maxβ的互补度级别相同的解，还须继续研究各个解组合的横向互补度，进而深入指导决策者。

6 结束语

本文通过对企业能力互补度的量化，将互补度系数引入选择规则中，对相同级别的互补度的解进一步引入相容性的判断，解决了在运用粒子群算法求解多目标选择过程中出现多个帕累托最优解的选择难题，在企业动态联盟伙伴选择过程中既考虑了短期目标，又考虑了再次联盟概率和利于企业成长的最佳共振环境等战略目标，实现动态中的相对稳定。本文在引入互补度决策时偏重于定量的纵向互补度，仅考虑了基于生产的伙伴选择问题。对于产品设计、营销、售后等供应链上下游的其他阶段的联盟伙伴选择，横向互补度值得进一步研究。

1 李允尧，生延超，姜向阳.联盟动机、技术能力与企业入盟的最优策略.管理世界，2010(3):178～179

2 Cao Q,Wang Q.Optimizing vendor selection in a two-stage outsourcing process.Computers&Operations Research,2007,34(12):3757～3768

3 Wang T C,Chen Y H.Applying fuzzy linguistic preference relations to the improvement of consistency of fuzzy AHP.Information Sciences,2008,178(19):3755～3765

4 Mikhailov L.Fuzzy analytical approach to partnership selection in formation of virtual enterprises.Omega,2002,30(5):393～401

5 Jharkharia S.Selection of logistics service provider:an analytic network process(ANP)approach.Omega,2007,35(3):274～289

6 Solesvik M Z.Partner selection for interfirm collaboration in ship design.Industrial Management&Data Systems,2010,11(5):701～710

7 张卫，潘晓弘，刘志等.基于云模型蚁群优化的制造服务调度策略.计算机集成制造,2012，18(1):201～207

8 Wu C,Barnes D.Formulating partner selection criteria for agile supply chains:a dempster–shafer belief acceptability optimization approach.International Journal of Production Economics,2010,125(2):284～293

9 Hassan M M,Song B,Huh E N.A market-oriented dynamic collaborative cloud services platform.Annals of Telecommunications,2010,65（11-12）:669～688

10 Cavusgil S T,Evirgen C.Use of expert systems in international marketing:an application forco-operative venture partner selection.European Journal of Marketing,1997,31(1):73～86

11 Mitsuhashi H,Greve H R.A matching theory of alliance formation and organizational success: complementary and compatibility.Academy of Management Journal,2009,52(5):975～995

12 黄彬，高诚辉，陈亮.模糊完工时间和模糊交货期下的虚拟企业伙伴选择.系统工程理论与实践,2010,30(6):1085～109

13 杨虎，张东戈，刘浩等.一种基于间接互惠的计算网格合作激励机制研究.电信科学,2011(9):42～47

14 任声策，宣国良.基于学习和能力互补动态的研发联盟稳定性研究.中国管理科学，2005,13(5):111～115

15 张海青，田军.IT人员业务能力与技术能力的互补性对企业竞争优势的影响.管理学报，2011,8(9):1359～1364

16 iiMedia Research:2012年Q3中国智能手机市场销量达到4980万部.http://www.199it.com/archives/83266.html

Research on Manufacture Partner Selection with Competence Complementary Operator

Ju Chunhua1,2，Fu Xiaokang3
（1.School of Computer Science and Information Engineering,Zhejiang Gongshang University,Hangzhou 310018,China;2.Center for Studies of Modern Business,Zhejiang Gongshang University,Hangzhou 310018,China;3.School of Business Administration,Zhejiang Gongshang University,Hangzhou 310018,China）

The main objective for enterprises alliances is to integrate complementary resources,and complementary degree is a crucial factor affecting the alliance stability and alliance performance,so it is meaningful to do research on thecomplementary degree in partner selection.Based on the characteristics of manufacture alliance,an evaluation coefficient was designed to access the competence complementary degree in manufacture alliances.Then a manufacture partner selection model was constructed with the evaluation coefficient,in which selection rules was built with the consideration of complementary degree.The problem was solved which stated in the model.Firstly,AHP was used to filter the disqualified enterprises.Secondly,particle swarm optimization (PSO)was applied to obtain the Pareto optimal solutions.Last but not the least,complementary degree evaluation coefficient was calculated to support selection decisions.Also,communications industry was used as an example to implement the proposed model in MATLAB and conclusions were given by analyzing the simulation results.

partner selection,complementary degree,PSO,Pareto optimal solution

10.3969/j.issn.1000-0801.2013.03.018

* 国家自然科学基金资助项目（No.71071141），教育部高等学校博士学科点专项科研基金资助项目（No.20103326110001），浙江省自然科学基金重点项目（No.Z1091224）

琚春华，男，博士，浙江工商大学计算机信息与工程学院、浙江工商大学现代商贸中心教授，浙江工商大学管理学院博士生导师，主要研究方向为智能信息管理、电子商务与物流的研究、决策支持系统等。

傅小康，女，浙江工商大学管理学院博士研究生、讲师，主要研究方向为决策支持系统、服务协同、供应链管理等。

2013-02-23）