无源雷达探测中的直达波提取方法

张 瑜，贺秋瑞

(河南师范大学物理与信息工程学院，河南新乡 453007）

无源雷达探测中的直达波提取方法

张 瑜，贺秋瑞

(河南师范大学物理与信息工程学院，河南新乡 453007）

直达波作为无源雷达探测系统中的参考信号，在传输过程中受到多径杂波和噪声的干扰，从而对系统的探测性能产生影响。利用参考通道接收到的混合信号中直达波的能量最大这一现实，提出用主分量分析的方法对混合信号进行降维处理，通过保留主分量，舍弃次分量，达到了提取直达波的目的。仿真结果表明:该方法可以有效的从噪声干扰和多径干扰中提取直达波，提纯效果较好，且操作简便易行。

无源雷达;直达波;主分量分析

0 引言

无源雷达探测系统以其优越的“四抗”特性成为各国争相研究的热点［1］。与传统雷达不同的是，无源雷达自身不发射电磁波，而是用第三方辐射源信号作为参考信号，通过检测分析目标反射的回波信号，来对目标进行探测与跟踪，因此无源雷达系统设置了接收第三方辐射源直达波信号的参考通道和接收目标回波的回波通道［2］。与传统雷达相同的是，无源探测系统信号处理的核心同样是参考通道和回波通道之间的相关处理［3］。参考信号的好坏直接影响后续信号的处理，从而影响整个无源探测系统的探测性能，因此直达波的提纯在整个系统的信号处理中尤为重要。在无源雷达探测系统中，直达波的获取只能从接收机接收到的数据来进行估计，然而针对复杂的多径信号和噪声的干扰，在传输信道和发射源信号都未知的情况下，仅由接收数据来获取直达波参考信号具有很大的难度。目前，通信信号处理中的一些算法已被用来处理连续波体制下无源探测雷达直达波获取中的多径问题，如复倒谱技术、自适应均衡技术［4-6］，但是在仅仅已知接收数据的前提下，恢复直达波要借助盲均衡算法［7］，目前采用最多的是恒模盲均衡以及其改进算法，虽然对直达波有很好的恢复效果，但是仅仅对特定的信号模型适用，限制了辐射源的选择。本文针对无源雷达探测系统中受多径杂波和噪声干扰的直达波提取问题，提出主分量分析提取算法。该方法的基本思想是:针对接收机接收到的数据中直达波能量最大的这一特性，利用主分量分析方法只提取主要分量而忽略次分量，对数据进行降维处理来提取直达波。

1 主分量分析提取直达波

1.1 接收混合信号的分析

直达波是用无源探测系统中的参考通道接收的，使参考通道接收天线的主瓣方向指向辐射源的方向，保证在天线接收时直达波的纯度尽可能的高，但是多径杂波和噪声同样也会从天线的主瓣和副瓣进入接收机从而对直达波形成噪声干扰［1］。在参考通道中，直达波信号、多径信号、噪声能量大小的关系，会因为辐射源的选择、距离辐射源的位置、布站方式等因素的不同而变化。但是直达波的能量最大这一关系是不变的［4］。

在无源探测系统中，把每条多径杂波和噪声信号都视为各由1个辐射源产生［8］，源信号向量设为S=(s1，s2，s3，…，sm）T，各个辐射源对系统的贡献率称为源信号si，在这里设s1为直达波信号，可知s1的能量最大。这些辐射源发射的信号经过线性的混合方式到达接收机，设接收机混合数据组成的向量X=(x1，x2，x3，…，xm）。用主分量分析的方法对 X 进行降维处理，只需提取出能量最大的信号，即为直达波信号的估计值。

1.2 主分量分析法

主分量分析 (PCA）是Pearson在1902年提出的。主分量被认为是输入数据中能量最大的成分，通常认为是重要的分量，它往往与传感器检测的主要物理量相对应，把从混合信号中求出主分量的工作称为主分量分析。PCA可用于对含有噪声的与高度相关的接收数据进行分析。把高维信息投影到低维子空间，并保留主要信息［9］。

式中，vi为∈ψ{v∶vTv=I}m维正交化向量集中的向量，且满足如下条件:

达到最大，当然该准则可扩展到n个主分量 (n取1～m之间的任意数）。

其中，计算混合数据的协方差矩阵Rxx的计算量很大，对矩阵直接进行对角化或特征值分解的代价也相当高，如果采用自适应算法不用计算或估计阶数很大的协方差矩阵Rxx，可以直接从输入向量确定出协方差矩阵的特征值以及对应的特征向量。若x为零均值的随机向量，在实际求解中，只能利用有限长的数据对协方差矩阵Rxx进行估计，即

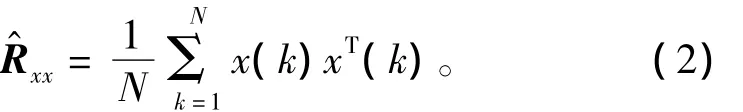
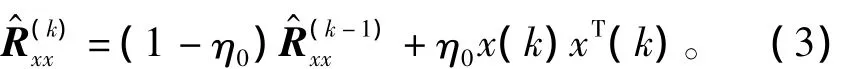
式中:η0＞0为学习速率;(1-η0）为遗忘因子。η0需根据信号的平稳性选取 (一般取0.01≤η0≤0.1），在对直达波提取时，会根据不同的信号类型进行选择。

其中N为数据长度。如果该协方差矩阵选用的数据长度N不变或者变化很缓慢，则可以使用滑动平均在线估计该协方差矩阵，即

1.3 基于主分量分析的直达波提取方法

由于无源雷达接收机接收到的各组观测数据之间可能有相关成分且均值可能不为0，因此需在求主分量之前首先进行零均值处理和白化预处理，具体方法在文献［10-11］中有详细说明，这里不再赘述。其次，求接收到的混合数据的协方差矩阵Rxx。根据所估计的协方差矩阵，求解全部的特征值λ1，λ2，…，λm和对应的特征向量v1，v2，…，vm，并将各特征值按从大至小的顺序排序，即λ1≥λ2≥…λm，以方差贡献率为参考，设置阈值，选择感兴趣的特征信号和对应的特征向量。针对本文直达波信号提取而言，因为在混合数据中，直达波的能量最大，因此选择最大的特征值λ1和对应的特征向量v1进行主分量的提取。最后，根据y1=vT1x提取出主分量，即为直达波信号。另外，由以上分析可知，只要观测数据满足主分量分析的前提条件，便可对无源雷达系统的直达波进行提取，而不受限可辐射源的选择。

2 仿真与分析

以基于调频广播辐射源的无源雷达系统为例，本文运用主分量分析的方法对其直达波进行提取仿真。采用调频广播信号模拟直达波信号，采样间隔设置为0.01 s，调制系数为200，载波是幅度为1 V，频率为2 000 Hz的正弦波，产生1个类似的声音信号控制的调频信号。采用2条多径信号为多径干扰，相对直达波的时延分别为0.01 s和0.001 s，信干比为-10 dB;噪声为高斯白噪声，信噪比为-10 dB。仿真时间为2 s。其直达波信号如图1所示。把每个信号当做1个辐射源，无源雷达接收系统采用4个接收机接收。接收的混合数据如图2所示。设置阈值为2.48，学习速率η0为0.03。通过主分量分析提取的直达波信号如图3所示。

由图1～图3可知，主分量分析可以对混合数据中的直达波信号进行有效提取。虽然主分量分析提取的信号在幅度上存在模糊性，但是对于无源探测系统来说，幅度的模糊性不影响后续的相关处理效果。

图1 调频广播的直达波信号Fig.1 The direct-path-wave of FM radio

图3 提取的直达波信号Fig.3 The extracted direct-path-wave

3 直达波提取的性能分析

为定量衡量本文提出的直达波提取方法的性能，采用提取信号和源信号的相似系数ρij作为性能指标，即

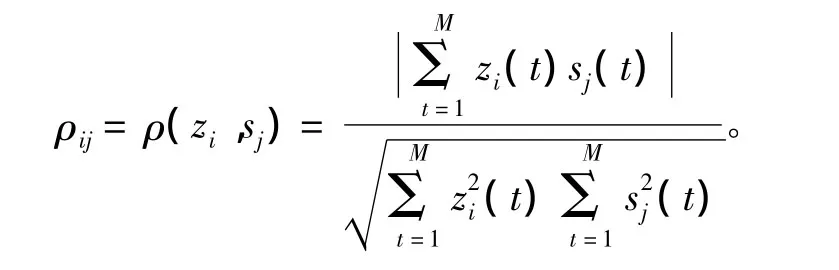
其中，zi为主分量提取方法提取出的信号;sj为源信号。若zi=csj，c是一个常数，且0≤ρij≤1，ρij越大表明所提取信号与源信号越接近。当ρij=1时，表明提取的信号与源信号仅在幅度上有差异;当ρij=0时，zi与sj之间不相关。在本文中，把多径信号干扰和高斯白噪声干扰都统称为噪声干扰，针对基于调频广播辐射源的无源雷达系统，分别采用复倒谱技术和主分量分析方法，对在不同噪声干扰的情况下提取直达波的性能进行仿真分析，如图4所示。由图可知，直达波信号在受到噪声干扰的情况下，采用基于主分量分析的提取方法提取的直达波信号和真实直达波信号的相似系数远高于复倒谱技术提取的相似系数。同样可以发现，信噪比越低，信号的相似系数也越低，为了得到更高纯度的直达波，需要致力于信噪比的提高。

图4 不同信噪比下的相似系数Fig.4 The similar coefficient ofwave in different SNR

4 结语

本文根据无源探测系统中参考通道接收到的混合数据中，直达波能量最大这一关系，提出用主分量分析的方法通过控制阈值保留主分量，舍弃次分量，对直达波进行提取，结果表明该方法提取效果较好，简单易行。但是对于控制主分量个数的阈值确定而言，需要人为调试，无疑为直达波的提取增加了工作量。若不用人为设置阈值便可自适应地选取主分量个数，将会使工作量大大减少，这是下一步需要研究的方向。

［1］宋杰，何友，复青，等.基于非合作雷达辐射源的无源雷达技术综述［J］.系统工程与电子技术，2009，31(9）:2151-2154.

SONG Jie，HE You，CAIFu-qing，etal.Overview of passive radar technology based on non-cooperative radar illuminator［J］.Systems Engineering and Electronics，2009，31(9）:2151-2154.

［2］阙俊才，王俊.基于GSM信号的无源雷达直达波方向估计［J］.火控雷达技术，2010，39(4）:27-30.

［3］左斌，赵洪立.无源探测雷达系统的现状及发展趋势浅述［J］.中国科技信息，2009(14）:52-53.

［4］朱家兵，洪一.基于复倒谱技术的无源雷达直达波提纯方法［J］.现代雷达，2007，29(8）:75-78.

［5］吴海洲，陶然，单涛.数字电视辐射源雷达基于空域滤波的直达波获取［J］.兵工学报，2009，30(2）:226-230.

［6］朱家兵，洪一，陶亮，等.基于自适应分数延迟估计的FM广播辐射源雷达直达波对消［J］.电子与信息学报，2007，29(7）:1674-1677.

ZHU Jia-bing，HONG Yi，TAO Liang，et al.Direct-path cancellation to FM broadcast transmitter radar based on adaptive fractional delay estimation［J］.Journal of Electronics＆ Information Technology，2007，29(7）:1674-1677.

［7］赵旦峰，许聪，张扬.基于二维恒模算法的直达波提纯技术［J］.雷达与对抗，2010，30(2）:6-8.

［8］张瑜，房少娟，李雪萍.低角雷达多径误差抑制的盲分离方法［J］.电光与控制，2011，18(10）:32-34.

ZHANG Yu，FANG Shao-juan，LI Xue-ping.Blind separation method of low-angle radar multipath error suppression［J］.Electronics Optics ＆ Control，2011，18(10）:32-34.

［9］张发启.盲信号处理及应用［M］.西安:西安电子科技大学出版社，2006.

ZHANG Fa-qi.Operation and Application of Blind Signal［M］.Xi'an:Xi'an University of Electronic Science and Technology Publishing House，2006.

［10］徐洪涛，王跃刚，蒲源，等.基于白化旋转技术的盲分离算法［J］.电光与控制，2010，17(7）:39-40.

［11］CHEUNG Y M，LIU H L.A new approach to blind source separation with global optimal property［C］.Proceedings of the IASTED international Conference of Neural Neural Networks and Computational Intelligence，Gridelwald，Switzerland，2004.137-141.

Research of a extraction method for direct-path-wave in passive radar detection

ZHANG Yu，HE Qiu-rui
(College of Physics and Information Engineering，Henan Normal University，Xinxiang 453007，China）

The direct-path-wave as the reference signal is affected by multi-path interference signals and noise in the passive radar detection system，and further influence the performance of the detection system.By adopting the reality of the direct-path-wave has the highest energy.A method of principal component analysis is proposed，which can reduce dimension of the mixed signals，retain the principal components，abandon theminor components，achieve the extraction of direct-path-wave aim.The simulation results show that the method can extract the direct-path-wave efficiently from the multi-path interference signals and noise，has the better extraction effect，and themethod is simple.

passive radar;direct-path-wave;principal component analysis

mixed signals of receiver

TP911

A

1672-7649(2013）03-0074-04

10.3404/j.issn.1672-7649.2013.03.016

2012-09-24;

2012-11-12

国家自然科学基金资助项目(61077037）

张瑜(1963-），男，高级工程师，主要从事微弱信号检测、射频识别、电磁波传播理论与应用等研究。

图2 接收机接收到的混合信号 Fig.2 Tthe