静水压下声学覆盖层声阻抗研究

邹明松，吴文伟，余晓丽，廖彬彬

(中国船舶科学研究中心，江苏无锡 214082）

静水压下声学覆盖层声阻抗研究

邹明松，吴文伟，余晓丽，廖彬彬

(中国船舶科学研究中心，江苏无锡 214082）

采用有限元方法计算静水压作用下声学覆盖层空腔的受压变形，采用多层均匀分布厚壁圆柱筒体的薄层来模拟声学覆盖层内复杂的空腔，用传递函数法推导多层介质的声传播矩阵列式。进一步结合实验所得不同静水压下声学覆盖层的材料特性参数，建立静水压作用下声学覆盖层声阻抗的求解方法。通过与某型声学覆盖层试验结果的比对分析，验证了本文所述计算方法的正确性。在此基础上，分析了静水压对声学覆盖层声阻抗的影响。

声学覆盖层;静水压;声阻抗

0 引言

声学覆盖层声振特性的研究起源于二战时期，由于其与潜艇隐身技术相关联，国外公开发表的文献较少。文献［1］针对Alberich型声学覆盖层的结构特点，利用一维模型对圆柱声腔的情况进行了研究。文献［2］用有限元方法分析了Alberich型声学覆盖层在平面波正入射时的反射特性。20世纪80年代中期以来，国内也陆续开展了这方面的研究［3－8］。文献［4］用传递矩阵法研究了水下材料复合层的吸声特性，将空腔的影响看作每个液态薄层的面积变化。文献［5］采用多层均匀分布厚壁圆柱筒体模型来模拟声学覆盖层，通过声学覆盖层声阻抗建立了圆柱壳—声学覆盖层—水介质耦合的声振模型。文献［7］应用传递矩阵法建立了复合过渡型声腔结构消声瓦吸声性能理论计算模型，分析了声腔结构形式、材料参数变化对消声瓦吸声性能的影响。文献［8］提出声学覆盖层声学性能等效参数模块化计算方法，采用有限元方法计算简单空腔模块的等效复波数，再利用传递矩阵法计算整个复杂空腔声学覆盖层的声学性能，该方法适用于多连通腔等复杂声学覆盖层声学性能的计算。文献［8］还对静水压下声学覆盖层材料特性参数测试进行了研究。不管是机理、实验技术还是设计层面，这些研究都突破了很多技术瓶颈。

本文在上述研究的基础上，将声学覆盖层在不同水温、水压下的材料特性参数测试，橡胶材料受压变形计算以及声学覆盖层空腔结构声传递解析计算相结合，完善了一套可计及水温、水压影响的声学覆盖层声阻抗计算方法。为验证计算方法的正确性，在不同静水压下，测试了一声学覆盖层的声阻抗，与理论计算结果进行了比对。

1 传递函数法研究多层介质中的波传播

工程中的声学覆盖层一般有复杂形状的内部空腔，本文用多层均匀分布圆柱形空腔的薄层来模拟。根据文献［5］，各层之间由于穿孔率不同，等效声学参数也不同，所以需要讨论多层介质中的波传播。在文献［5］中，用传递函数法研究了空间域的多层声介质中的波传播:

声学覆盖层内部各层之间满足各层间边界条件:在相交面处的压力平衡，法向速度连续。因此，将每层的传递函数矩阵连乘:

2 声学覆盖层声振传递参数的推导

采用如图1(a）所示的模型来描述声学覆盖层的声振传递关系［5］。对声学覆盖层的内部腔体进行分层，将每层处理成1个均匀的厚壁圆柱筒体，如图1(b）所示。图2所示轴对称弹性厚壁筒体的振动方程为

图1 声学覆盖层理论分析模型Fig.1 Theoretical analyticmodel of acoustic coating

图2 柱坐标系下的声学覆盖层单元体ig.2 Cell of acoustic coating in cylindrical coordinate system

式中:a和b为厚壁筒体内、外半径;ρa，ur，w，λ，μ分别为声学覆盖层的密度、厚壁筒体的径向位移、轴向位移和拉梅系数;σrz和σrr分别为单元体内剪应力、正应力。

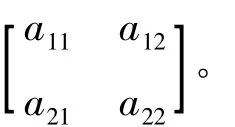
静水压作用下，声学覆盖层内空腔将受压变形，穿孔率ε将发生变化，即声振传递矩阵也相应改变。

3 静水压引起的消声瓦内空腔变形

采用比较常用且较精确的2个参数Moony-Rivlin模型来描述声学覆盖层在静水压作用下的静变形［8］，即

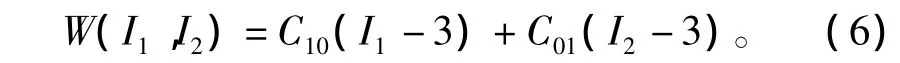
式中:W为应变能密度;I1和I2分别为第一、第二Green应变不变量;C10和C01为Rivlin系数，均为正定常数。2个参数模型在变形很大的范围内也基本满足要求。

工程上C10与C01的获得，可以通过材料试验机上进行的单轴拉伸或压缩试验，也可以根据材料的硬度进行粗略估计［9－10］。

采用前述的厚壁筒体模型，利用有限元软件计算声学覆盖层空腔在静水压作用下的变形，材料特性取Moony-Rivlin模型。

4 计算结果与试验结果比对

在702所水声声管内测试一50mm厚的丁苯橡胶制声学覆盖层的声阻抗，内部空腔呈喇叭形。为更好地说明本文所述方法的正确性，材料特性参数采用上海交大水声声管内的测试数据［8］，测试样品也是丁苯橡胶，但空腔呈圆柱形。二者测试水温相同。

声学覆盖层声阻抗测量在702所声管实验室中的中频管内进行，整个测试系统有一套完备的压力和温度控制系统。实验测试系统框架见图3，由计算机控制信号的发射、采集分析和记录。

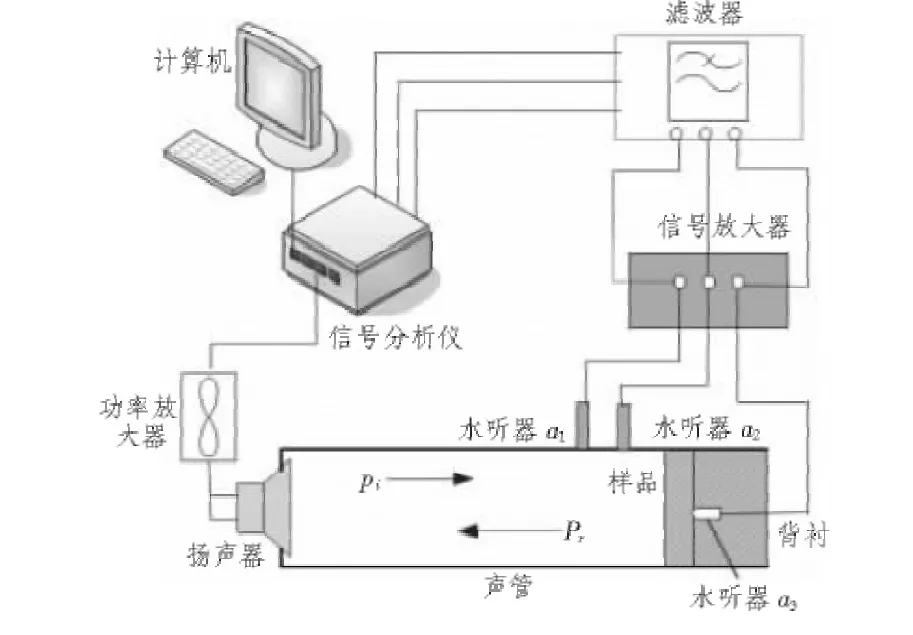
图3 实验测量系统装置示意图Fig.3 Diagrammatic sketch of experimental facility

定义消声瓦声阻抗矩阵 ［Z］的具体形式为

图4是有限元分析所得试验样品空腔受压变形图。

图4 试验样品内部空腔受压变形图Fig.4 Compressed deformation of test sample's cavity

分考虑空腔受压变形和不考虑空腔受压变形2种情况计算该声学覆盖层的声阻抗，结果如图5～图8所示，图中ρ0和c0分别为流体的密度和声速。可见:计算结果与试验结果吻合较好，空腔受压变形对声学覆盖层声阻抗有较大的影响。

图5 静水压为1 MPa时z11和z22随频率变化Fig.5 Variation of z11 and z22 with frequencies at 1 MPa hydrostatic pressure

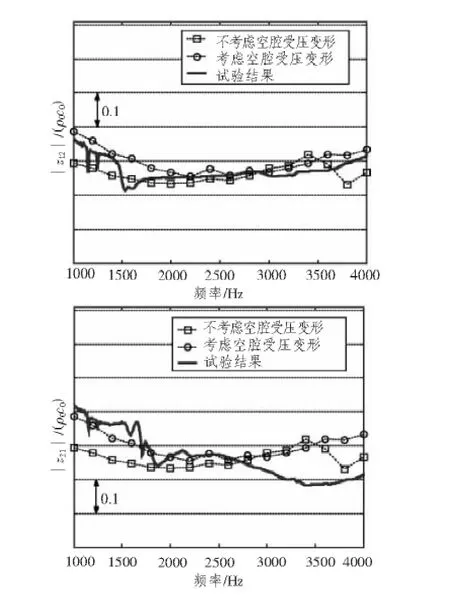
图6 静水压为1 MPa时z12和z21随频率变化Fig.6 Variation of z12 and z21 with frequencies at1 MPa hydrostatic pressure

图7 静水压为2 MPa时z11和z22随频率变化Fig.7 Variation of z11 and z22 with frequencies at2 MPa hydrostatic pressure

图8 静水压为2 MPa时z12和z21随频率变化Fig.8 Variation of z12 and z21 with frequencies at2 MPa hydrostatic pressure

5 结语

本文将试验测量、有限元分析及解析求解三者相结合，完善了静水压作用下声学覆盖层声阻抗的求解方法。通过与一声学覆盖层试验结果的比对，验证了本文所述计算方法的正确性。并通过分析得出如下结论:

1）本文所述的计算方法可为声学覆盖层选材、结构尺寸等方面的优化设计提供手段;

2）静水压引起声学覆盖层内部空腔受压变形，对其声阻抗有较显著的影响。

［1］GAUNAURD G.One-dimensionalmodel for acoustic absorption in a viscoelastic medium containing short cylindrical cavities［J］.Journal of the Acoustical Society of America，1977，62(2）:298 －307.

［2］EASWARAN V，MUNJAL M L.Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers:a finite element approach［J］.Journal of the Acoustical Society of America，1993，93(3）:1308 －1318.

［3］朱蓓丽，任克明.等效参数法研究带圆柱通道橡胶体的声学性能［J］.上海交通大学学报，1997(7）:20－25.

ZHU Bei-li，REN Ke-ming.Acoustic properties analysis of elastomer with cylindrical bores using equivalent parametric method［J］.Journal of Shanghai Jiaotong University.1997(7）:20－25.

［4］何祚镛，王曼.水下非均匀材料复合层吸声特性研究［J］.应用声学，1996，15(5）:6 －11.

HE Zuo-yong，WANG Man.Study on properties of sound absorption of underwater non-uniform material composite layer［J］.Journal of Application Acoustic，1996，15(5）:6 －11.

［5］殷学文.敷设消声瓦的双层加肋圆柱壳的振动和声辐射研究［D］.无锡:中国船舶科学研究中心，2001.

YIN Xue-wen.Study on vibration and acoustic radiation from two concentric ring-reinforced cylindrical shells covered with sound-absorbing layers［D］.Wuxi:China Ship Scientific Research Center，2001.

［6］王曼.水声吸声覆盖层理论与试验研究［D］.哈尔滨:哈尔滨工程大学，2004.

WANG Man.Theory and experimental study on underwater anechoic layer［D］.Harbin:Harbin Engineering University，2004.

［7］陈建平.消声瓦声学性能计算方法研究［J］.噪声与振动控制，2007(4）:123－126.

CHEN Jian-ping.Study on the computation method of anechoic tile acoustical characteristic［J］.Journal of Contral of Noise and Vibration，2007(4）:123 －126.

［8］胡碰.静水压力下声学覆盖层声学性能模块化方法研究［D］.上海:上海交通大学，2008.

HU Peng.Study on acoustic performance of acoustic layer under hydrostatic pressure with modularity method［D］.Shanghai:Shanghai Jiaotong University，2008.

［9］郑明军，王文静，等.橡胶Mooney-Rivlin模型力学性能常数的确定［J］.橡胶工业，2003，50(8）:462 －465.

ZHENGMing-jun，WANGWen-jing，et al.Determination for mechanical constants of rubber Mooney-Rivlin model［J］.Rubber Industry，2003，50(8）:462 －465.

［10］王伟，邓涛，等.橡胶Mooney-Rivlin模型中材料常数的确定［J］.特种橡胶制品，2004，25(4）:8 －10.

WANGWei，DENG Tao，et al.Determination for material constants of rubber mooney-rivilin model［J］.Special Purpose Rubber Products，2004，25(4）:8 －10.

Calculation of acoustic coating's Impedance under hydrostatic pressure

ZOU Ming-song，WUWen-wei，YU Xiao-li，LIAO Bin-bin
(China Ship Scientific Research Center，Wuxi214082，China）

The finite elementmethod is adapted to caculate the deformation of acoustic coating under hydrostatic pressure in this paper.The complicated cavity inside the acoustic coating ismodeled by uniformly distributing thin cylindrical layer and the acoustic propagation matrix is deduced by using transfer function method.Combining tested material characteristic parameters of acoustic coating under different hydrostatic pressures，the computing method of the acoustic impedance of acoustic coating is finally constructed.The computing method is verified by the experimental results of certain acoustic coating.Based on the computing method，the influence of hydrostatic pressure on acoustic impedance is analyzed.

acoustic coating;hydrostatic pressure;acoustic impedance

TB53

A

1672－7649(2013）03－0057－04

10.3404/j.issn.1672－7649.2013.03.012

2012－03－30;

2012－08－10

邹明松(1982－），男，博士研究生，工程师，从事深海空间研究。