图的相对结合数与图的结构的两个新结果
邓毅雄,曾爱祥
(1.华东交通大学软件学院,江西南昌 330013;2.江西省新干县湖中学,江西吉安 331303)

文中用到的几个记号的说明:设有图G1,G2,G3,我们用G1+G2表示G1中各点与G2中各点分别邻接所得之图,即V(G1+G2)=V(G1)∪V(G2),E(G1+G2)=E(G1)∪E(G2)∪{e|e=uv,u∈V(G1),v∈V(G2)};用G1+G2+G3表示G1中各点与G2中各点分别邻接,而G2中各点与G3中各点亦分别邻接所得之图,其它情形类似定义。设S是G的一个点集,用G[S]表示S在G中的生成子图,即V(G[S])=S,E(G[S])={e|e=uv,u,v∈S,且e∈E(G)}。以下我们用Fm表示所有可能的m阶图中的某一个图。用δ(G)表示图G的最小度,∅为空集符号。
在对图的相对结合数的讨论中,考虑满足rb(G)=k的图类是一个非常有趣的问题,在文献[3-5]中,对这方面问题进行了一定讨论,本文对这个问题的进一步讨论,得到了两个相关的结果。下面我们首先将文献[3-4]中的有关结果归纳如下:
定理1[4]对任意2-n≤k≤n-2,k≠3-n或n-3,存在n阶连通图G,使rb(G)=k。
定理2[3]设G是n阶连通图(n≥2),则rb(G)=2-n当且仅当G=Kn;rb(G)=n-2当且仅当G=K1,n-1。
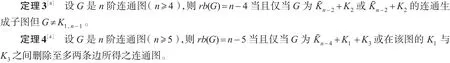
1 主要结果
定理5 对任意n阶(n≥6)连通图G,rb(G)=n-6当且仅当G为下列图之一:

定理6 对任意n阶(n≥4)连通图G,则rb(G)=4-n当且仅当G具有如下结构之一:

2 定理证明
定理5的证明 首先我们注意到,若G取得定理所给出的图,易于验证它们均满足rb(G)=n-6,也即充分性成立,定理的证明关键是其必要性。


图1 满足情形1.2的所有可能的4阶图Fig.1 The graphsof order 4 that content case 1.2
情形1.2.1 若G[V(S∪N(S))]=2K2,即为图1(a),则由G的连通性,N(S)={u}对应的K1与G[V(S∪N(S))]的2K2的邻接关系只能为如图2(a)(b)(c)所示情况之一。

图2 K1与2K2的邻接关系Fig.2 Ad jacent relationship of K1 and 2K2




图3 一类不满足rb(G)=n-6的图Fig.3 A classgraph of discontent rb(G)=n-6




[1]CHARTRAND G,LESNIAK L.Graphsand digraphs[M].3 rd ed.London:Chapman&Hall,1996:1-106.
[2] JA BONDY,USR MURTY.Graph theory w ith application[M].New York:Elsevier Science Publishing Company,1976:1-65.
[3]邓毅雄.图的相对结合数[J].华东交通大学学报,1995,12(1):92-96.
[4]邓毅雄.图的相对结合数的进一步结果[J].华东交通大学学报,1997,14(1):64-69.

