斜拉桥成桥索力优化理论及方法的最新进展

田 源 杨海霞

（河海大学力学与材料学院，南京 210098）

斜拉桥是将斜拉索两端分别锚固在塔和梁或其他载体上，形成塔、梁、索共同承载的结构体系［1］.从1956年第一座斜拉桥－瑞典的Stromsund桥建成以来［2］，至今全世界已建成400多座斜拉桥，其中中国有100多座.近年来，斜拉桥因跨径大、造型美成为桥梁工程中最具竞争力桥梁之一.其中，斜拉索被称作是斜拉桥的生命线，可以通过调整索力来改善主梁和塔的受力，从而达到结构受力、斜拉桥索力、线形等与设计理想状态基本吻合的合理成桥状态［3］.要达到斜拉桥的合理成桥状态，首要问题是确定其成桥索力.目前，国内外学者就成桥索力优化问题，提出了多种切实可行的优化方法.

1 成桥索力优化理论

从Schmit用数学规划方法解决结构优化设计算起，结构优化设计作为一门独立的学科出现有40多年的历史［4］.优化设计概括起来主要包括两方面内容：一是将设计问题的物理模型转化为数学模型，二是采用适当的优化方法解答数学模型.虽然结构优化设计在桥梁工程中起步较晚，但近些年，随着计算机技术的高速发展，许多行之有效的桥梁结构优化方法也相继出现.其中，对于高次超静定结构的斜拉桥，其索力的改变对结构内力影响明显，合理成桥状态索力的研究成为斜拉桥设计的重点［5］.

斜拉桥索力优化的概念可以通过索梁一次超静定结构［6］加以说明，索梁结构如图1所示.

主梁弯矩方程

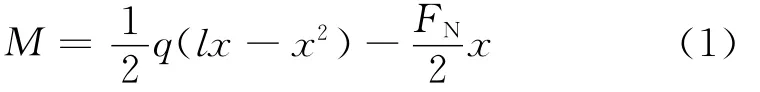
式中，FN为拉索索力，q为主梁自重集度，l为梁跨径.如果拉索不张拉，考虑变形协调条件

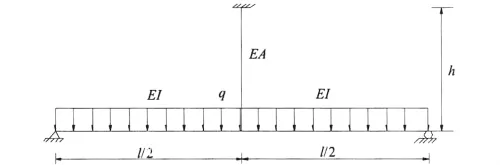
图1 索梁一次超静定结构

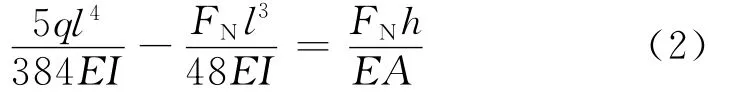
得到索力

图2 索力优化前主梁弯矩图

为了优化主梁受力，可选取主梁弯矩平方和为目标函数

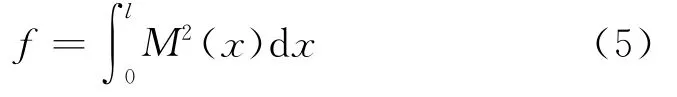
将式（3）和式（4）代入式（5），得到该目标函数，取驻值即f＝0时的索力

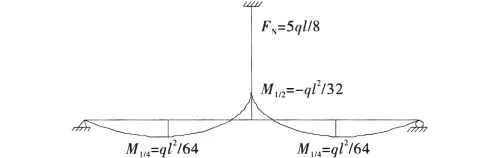
图3 索力优化后主梁弯矩图

斜拉桥索力优化根据研究内容的不同可分为成桥索力优化和施工索力优化两类［7］.本文只针对合理成桥状态索力优化方法进行总结和比较.从是否考虑其斜拉桥几何非线性影响的角度，可将成桥索力确定方法分为两大类.其中，忽略几何非线性影响的优化方法包括指定受力状态法中的刚性支承连续梁法［8］、零位移法［8］和应力平衡法［9］等，无约束索力优化法中的弯矩平方和最小法［10］和弯曲能量最小法［11］等，有约束索力优化法中的用索量最小法［12］等，还有较综合的方法如影响矩阵法［13］.考虑几何非线性影响的优化方法有凝聚函数法［14］、一阶分析法［15］、序列二次规划法［16］等.

2 忽略几何非线性影响的成桥索力优化方法

斜拉桥成桥索力最先的确定方法都是从中小跨径斜拉桥开始的，从最初的刚性支承连续梁法到较为完备的影响矩阵方法，国内外学者提出了多种成桥索力优化方法.

2.1 刚性支承连续梁法

刚性支承连续梁法是由德国著名桥梁专家F.Leonhardit提出，其基本原理是让斜拉桥主梁的成桥恒载内力状态达到刚性支承连续梁的受力状态［17］.具体计算思路：将斜拉桥提供的弹性竖向支承视为刚性竖向支承，以斜拉桥主梁在恒载作用下弯矩呈刚性支承连续梁状态为优化目标，求出各支点反力，再利用斜拉桥竖向分力与刚性支点反力相等得优化索力.因力学原理简单、目标函数只涉及主梁，刚性支承连续梁法是最早使用的、最直观的合理成桥状态分析方法.又因成桥状态接近“稳定张拉力”，可减小混凝土徐变对成桥内力的影响，但未顾及索和塔的内力和位移状态，得出的索力可能过于不均匀，对主跨与边跨不平衡结构［18］、密索体系等会得出不够合理的恒载索力状态.

在刚性支承连续梁法的基础上，人们提出了其他指定受力状态或位移状态的优化方法［19］.如零位移法，以结构在恒载作用下索梁交接处位移为零为目标函数.此方法对于支架一次落架的斜拉桥，因考虑索的水平分力的影响，能得到比刚性支承连续梁法更合理的结果.然而，就悬拼与现浇结构而言，零位移法无意义.对于不对称结构因很难考虑索塔的弯矩，零位移法并不是行之有效的方法［20］.后来提出的内力平衡法［21］，因综合考虑了恒载和活载的共同作用，受力状态更合理，解决了主梁弯矩局部不合理问题，但仍会产生索力不均匀问题.

2.2 弯曲能量最小法

无约束索力优化方法中最常用的是最小弯曲能量法［22］.其计算原理是通过取斜拉桥塔、墩和主梁的弯曲应变能最小为设计目标函数来求得恒载下的合理成桥索力值［23］.在具体应用时，让索塔梁的轴向刚度取最大，梁和塔的的弯曲刚度不变，把全部荷载加在结构上，所得内力状态即为所求.该法综合考虑了主梁、塔、墩的受力状态，使整个斜拉桥内力在最大程度上均匀分布，所以求出的结果弯矩较小，索力也较均匀，但部分边索可能索力过小.此外，弯矩能量最小法只可考虑恒载作用，无法将活载和预应力影响考虑在内，需与其他索力优化方法结合才能得到更精确的索力优化结果.与最小弯曲能量法原理一致的是弯矩平方和最小法，其目标函数取结构（梁、塔、墩）弯矩平方和.弯曲能量最小法与弯矩平方和最小法相比，前者可以反映抗弯刚度对弯矩的权效应.

2.3 用索量最小法

用索量最小法是有约束索力优化方法中的一种，以斜拉桥的拉索用量（张拉力×索长）为性能指标函数，以主要截面内力、位移限制为约束条件来优化索力.由于该法的目标函数是斜拉桥受力的次要目标，所以对约束条件的要求相对较高.此法可考虑恒活载的共同作用，但仅以拉索量为目标函数不尽合理，合理约束方程的确定需考虑多方面因素.

有约束索力优化方法还包括最大偏差最小法［24］，一种以可行域中参量与期望值偏差为目标函数，如以斜拉桥梁和塔的最大应力最小为目标对索力进行优化.这种目标函数下得到的梁和塔应力分布均匀且最小，又因该法针对应力，结果比较直观，但目标函数不能显式表达，对优化方法有一定要求.

2.4 影响矩阵法

影响矩阵法综合了指定受力状态优化法、无约束优化法和有约束优化法3类优化方法，是较为完备的索力优化理论［25］.该法取斜拉桥关心截面的内力、应力、位移为受调向量｛D｝，斜拉索索力为施调向量｛X｝，通过影响矩阵［C］建立受调向量与施调向量的关系，将索力优化问题转化为线性代数方程

同济大学的肖汝诚给出了整个结构弯曲能量最小时最优索力与弯曲影响矩阵的关系［13］，并指出方程中各个变量在不同情况下的意义，同时导出恒、活载共同作用下的索力优化情形［26］.因为影响矩阵法计入了各种因素的影响，不以单一目标来表示，所以优化结果更加合理.但是仅仅采用影响矩阵法，难以综合考虑恒活载共同作用下梁、塔和索受力要求的受调向量.

3 计入几何非线性影响的成桥索力优化方法

随着苏通大桥以及香港Stonecutters大桥的建设，斜拉桥的跨径记录突破了1 000m.随着斜拉桥的跨度不断增大，其成桥索力优化设计有必要考虑其几何非线性的影响［27］.究竟多大跨径的斜拉桥才需考虑几何非线性，没有明确的界定，一般根据桥梁结构的整体刚度而定，对于整体刚度较柔的钢斜拉桥和结合梁斜拉桥跨径较大时需考虑几何非线性.就混凝土斜拉桥而言，跨径大于200m或刚度较柔时应计入非线性影响［8］.由于大位移、梁柱效应、斜拉索垂度等非线性因素［28］的影响，其目标函数和约束条件很难用索力的显式形式表达，属于非线性规划范畴.此时，可采用的索力优化方法有凝聚函数法、一阶分析法、序列二次规划法等.

3.1 凝聚函数法

凝聚函数法是一种求解非线性极大极小值的有效方法［29］.Templeman［30］、李兴斯等学者利用最大熵［31］原理，通过加权求和法导出一个可微函数，即为凝聚函数.相关文献也分别对凝聚函数法进行收敛性分析［32］及稳定性分析［33］.将此算法借用于斜拉桥索力优化中时，以不变形预张力［24］为基础，将斜拉桥合理成桥状态索力确定问题归结于一个多目标、多约束的非线性规划问题，再借用改进的基于熵原理凝聚函数法将多个目标、多个约束分别等价成一个光滑可微的目标和约束函数.

在此基础上，采用乘子惩罚函数法［4］进行求解，将有约束优化问题转化为无约束优化问题，再采用变尺度法［4］进行求解.凝聚函数法避免了传统方法求解规模大，收敛速度慢的缺点，但需结合其他优化算法如乘子惩罚函数法、变尺度法等，计算步骤比较复杂.

3.2 一阶分析法

在优化过程中，需使用目标函数对设计变量的偏导数因而称为一阶分析法［35］.其基本原理是以斜拉桥主梁和索塔的弯曲应变能为目标函数，以各斜拉索的索力为设计变量，结构应力和索力约束条件为状态变量，形成有约束的非线性规划问题.也可通过目标函数添加罚函数，将有约束问题转化为无约束问题.该算法在每次迭代中，需选择合适的搜索方向以及找到沿搜索方向合适的步长.搜索方向可由最速下降法或共轭方向法［4］确定，步长可通过黄金分割法［4］和最小二乘法［36］来确定.因为一阶分析法是基于目标函数对设计变量的敏感程度，所以更能得到精确的优化分析结果.该法适用于因变量很大，设计空间也相对较大，在大型有限元计算软件ANSYS中有较好的运用［37］.但该法在每次迭代过程中还有子迭代，如搜索方法以及梯度计算，使得一次优化迭代有多次分析循环，导致计算速度稍慢.

3.3 序列二次规划法

序列二次规划法是20世纪80～90年代发展起来的一种全局收敛且快速收敛的优化方法，该法是把非线性规划化为一系列二次规划来求解［4］.近几年，简金宝又提出了适当条件下超线性和二次收敛的强次可行序列二次规划法［38］.该法通过建立索力优化的非线性规划模型，以斜拉桥主梁和索塔的弯曲应变能为目标函数，以各斜拉索的索力为设计变量，结构的应力和索力为约束条件，采用强次可行序列二次规划法进行优化求解，确定斜拉桥合理成桥状态的索力.强次可行序列二次规划法计算量小，具有全局收敛性、强收敛性、超线性、二次收敛性的优点.并且该算法的初始点可任取，无需使用某种函数作线性搜索，这样需要的计算次数有限，同时可考虑结构的非线性影响，可计入斜拉桥调索过程中对索力、应力、弯矩等不同性态的约束，适用于多单元、多工况、多设计变量斜拉桥合理成桥状态确定问题.当然，序列二次规划法对算法设计、程序编制要求很高.

4 多种成桥索力优化方法比较

从斜拉桥这种桥型出现起，成桥索力优化方法的确定一直是国内外学者反复研究的课题.到现在为止，已出现了多种方法.方法的多样性，一方面说明了人们对斜拉桥的认识比较深刻，比较全面；另一方面也说明了每一种方法都有其适用范围，还没能找到解决斜拉桥成桥索力优化问题的一种统一方法.现对合理成桥索力优化问题的相关分析方法进行优缺点、适用情况总结，结果见表1.

表1 合理成桥状态索力优化方法比较分析

由表1可见，对于不需考虑几何非线性影响的斜拉桥结构，可采用刚性支承连续梁法、弯曲能量最小法及影响矩阵法等.当斜拉桥活载内力占截面总内力15%～25%时［39］，需同时考虑活载作用，此时可采用内力平衡法、用索量最小法等.对于边跨与主跨不对称结构不宜采用零位移法.当设计对象为大跨度斜拉桥时，几何非线性作用明显，则需采用凝聚函数法、一阶分析法及序列二次规划法等.

5 成桥索力优化方法的发展方向

确定斜拉桥合理成桥状态索力的方法多种多样，就每一种方法而言，总存在一些不足，如弯曲能量法只能计算恒载作用下的，影响矩阵法只能采用线性叠加等.因此，各种综合方法也不断出现.唐密、左德中［40］采用最小弯曲能量法初定成桥状态，再用力平衡法确定主梁的弯矩可行域，使指定受力状态法与无约束优化方法得到很好的结合.杨俊［39］将主梁视作刚性支承连续梁，并引入索力对主梁弯矩的影响矩阵，将影响矩阵法做了一定改进.张文献等［41］增加主梁合理弯矩可行域的约束条件，以弯曲能量最小法计算，在假定主梁弯矩基本不变的前提下，用影响矩阵法调匀，有效地将3种优化方法综合，避免了各种单一方法的缺点，利用了各自的优点.谢支钢、赵拥军［42］先根据零位移法初定索力，再考虑恒活载的共同作用的应力平衡法确定主梁弯矩的合理恒载可行域.当然也有一些新颖方便的优化方法出现.吴轶雄［43］借用了拱桥设计的假载法，取准永久活载值的某系数值作为假载作用于结构，一般取车辆荷载满布且均布于全桥，以恒荷载和假载共同作用下的梁弯曲应变能最小为优化目标.郭钟群等［6］采用了可行域法对斜拉桥索力进行调整并用Matlab进行编程计算.陈素君等［44］提出在索力常规迭代法的基础上，从迭代初值的选取和迭代加速的超松弛法两方面加速迭代的初始平衡构型确定法.李文［45］将虚拟温度迭代法引入斜拉桥空间模型中，并考虑几何非线性的影响进行调索计算.

综上所述，根据斜拉桥的跨径、结构形式、设计要求、计算精度要求等的不同，已经形成了多种斜拉桥成桥索力优化实用方法.指定受力或位移状态的索力优化法中的内力平衡法最适合应用于上下对称截面的结构中，充分发挥材料的性能，还可考虑恒活载的共同作用；无约束优化方法中的弯曲能量最小法可以很好地解决不需要考虑活载作用的斜拉桥索力优化问题，求得的弯矩较小，索力较均匀；有约束优化方法中的用索量最小法适用于恒活载作用下梁和塔的内力和位移较易表达的情况；影响矩阵法可应用于几何非线性影响不明显的斜拉桥索力优化问题中，计入各种因素影响，不以单一目标表示；凝聚函数法、一阶分析法及序列二次规划法，可应用于几何非线性明显的大跨度斜拉桥成桥索力优化中，能适应大设计空间计算.其中，一阶分析法还在大型有限元软件ANSYS中有所体现［46］，凝聚函数法及序列二次规划法可借助相关软件进行编程计算.对于具体的斜拉桥成桥索力，可以选择合适的解决方案，必要时还可将上述方法适当结合，采用综合法.也可考虑假载法、虚拟温度迭代法等较易实现的方法.

虽然现已具有多种斜拉桥成桥索力优化方法，但还未找到一种能考虑多种因素、有较大适用范围的统一方法.今后的研究工作主要有两方面：其一，在满足斜拉桥索力均匀分布、主梁弯矩控制在可行域内、主塔弯矩不能太大、适当考虑活载等设计准则的基础上，能找到斜拉桥设计中所关心的更有效的可调目标.其二，随着斜拉桥跨径的增大，其几何非线性也影响着调索结果，需结合大型商业软件ANSYS、MIDAS等对计算模型进行更精确的模拟以及采用编程软件Matlab、FORTRAN等编写更有效的优化算法.

6 结 语

本文从是否计入几何非线性影响两方面介绍了斜拉桥成桥索力优化采用的基本方法，并对各种方法的优缺点及适用情况进行了较为系统的评论，总结了一些综合索力优化方法及特殊优化方法.随着计算机技术的不断发展、结构优化设计理论的研究不断深入以及斜拉桥成桥索力优化方法的不断探索，会形成计算精度更高、计算速度更快、运用范围更广的合理成桥状态优化方法，从而进一步满足斜拉桥设计要求及工程实际需要，达到桥梁设计安全、经济、美观的目标.

［1］ JTG／T D65－01－2007.公路斜拉桥设计细则［S］.北京：人民交通出版社，2007.

［2］ 林元培.斜拉桥［M］.北京：人民交通出版社，2004：1－4.

［3］ 项海帆.高等桥梁结构理论［M］.北京：人民交通出版社，2001.

［4］ 任旭华.现代工程设计方法［M］.北京：清华大学出版社，2009：26－103.

［5］ Zhang T，Wu Z.Dead Load Analysis of Cable－Stayed Bridge［C］／／International Conference on Intelligent Building and Management［J］.Singapore，2011，5：270－274.

［6］ 郭钟群，谢志华，赵 奎，等.基于可行域法的斜拉桥索力优化［J］.江西理工大学学报，2012，33（3）：10－13.

［7］ 王永安，刘世同，谭红梅，等.斜拉桥索力优化理论研究［J］.公路，2006（05）：31－34.

［8］ 刘士林，王似舜.斜拉桥设计［M］.北京：人民交通出版社，2006：89－94.

［9］ 颜东煌，李学文，刘光栋，等.用应力平衡法确定斜拉桥主梁的合理成桥状态［J］.中国公路学报，2000，13（3）：49－52.

［10］范立础，杜国华，马健中.斜拉桥索力优化及非线性理想倒退分析［J］.重庆交通学院学报，1992，11（1）：1－12.

［11］杜国华，姜 林.斜拉桥的合理索力及其施工张拉力［J］.桥梁建设，1989（3）：11－17.

［12］陆 楸，徐有光.斜拉桥最优索力的探讨［J］.中国公路学报，1990，3（1）：38－48.

［13］肖汝诚，项海帆.斜拉桥索力优化的影响矩阵法［J］.同济大学学报，1998，26（3）：235－240.

［14］杜蓬娟，张 哲，谭素杰.斜拉桥合理成桥状态索力确定的优化方法［J］.公路交通科技，2005，22（7）：82－85.

［15］张建民，肖汝诚.斜拉桥合理成桥状态确定的一阶分析法［J］.力学季刊，2004，25（2）：297－303.

［16］陶 海，沈祥福.斜拉桥索力优化的强次可行序列二次规划法［J］.力学学报，2006，38（3）：381－384.

［17］Edward B.Basic Influence Line Equations for Continuous Beams and Rigid Frames［J］.Journal of Structural Engineering，2000，5（2）：132－139.

［18］Lee T Y，Kim Y H，Kang S W.Optimization of Tensioning Strategy for Asymmetric Cable－stayed Bridge and its Effect on Construction Process［J］.Structural and Multidisciplinary Optimization，2008，35（6）：623－629.

［19］Chen D W，Au F T K，Tham L G，et al.Determination of Initial Cable Forces in Prestressed Concrete Cable－stayed Bridges for Given Design Deck Profiles Using the Force Equilibrium Method［J］.Computer ＆Structures，2000，74（1）：1－9.

［20］Wang P，Tseng T，Yang C.Initial shape of cable－stayed bridges［J］.Computers ＆Structures，1993，47（1）：111－123.

［21］陈德伟，范立础.确定预应力混凝土斜拉桥恒载初始索力的方法［J］.同济大学学报，1998，26（2）：120－124.

［22］Janjic D，Pircher M，Pircher H.Optimization of Cable Tensioning in Cable－Stayed Bridges［J］.Journal of Bridge Engineering，2003，8（3）：131－137.

［23］Sung Y－C，Chang D－W，Teo E－H.Optimum post－tensioning cable forces of Mau－Lo Hsi cable－stayed bridge［J］.Engineering Structures，2006，28（10）：1407－1417.

［24］Toril K，Ikeda K.Study of the Optimum design Method for Cable－stayed Bridge［J］.International conference on Cable－stayed Bridge，1987：1128－1139.

［25］张峻峰，丁志威，罗学成.基于影响矩阵法的斜拉桥成桥索力优化［J］.交通科技，2011，246（3）：4－6.

［26］肖汝诚，项海帆.斜拉桥索力优化及其工程应用［J］.计算力学学报，1998，15（1）：118－126.

［27］Hassan I A，Hegab.Parametric Investigation of Cable－Stayed Bridge［J］.Journal of Structure Eng，1998，114（8）：784－792.

［28］Ren W X.Ultimate Behavior Of Long－Span Cable－Stayed Bridges［J］.Journal of Bridge Engineering，1999，4（1）：30－37.

［29］李兴斯.解非线性极大极小问题的凝聚函数法［J］.计算结构力学及其应用，1991，8（1）：85－92.

［30］Andrew B T，Li X.A Maximum Entropy Approach to Constrained Nonlinear Programming［J］.Engineering Optimization，1987，12（3）：191－205.

［31］宋协武，王海军.约束多目标优化问题的区间极大熵方法［J］.徐州工程学院学报，2005，20（1）：69－72.

［32］唐焕文，张立卫.凸规划的极大熵方法［J］.科学通报，1994，39（8）：682－684.

［33］张玉忠，周广路，王长钰.非线性规划中凝聚函数法的稳定性［J］.运筹学学报，1997，1（1）：54－58.

［34］钟万勰，刘元芳，纪 峥.斜拉桥施工中的张拉控制和索力调整［J］.土木工程学报，1992，25（3）：10－15.

［35］赵 秋，邢 昕，翟慧娜.基于一阶优化方法的钢－混凝土组合索塔锚固区结构设计［J］.石家庄大学学报：自然科学版，2010，23（4）：26－31.

［36］Zhang H，R.Com A，Scheinberg K.A Derivative－Free Algorithm for Least－Squares Minimization［J］.Society for Industrial and Applied Mathematics，2010，20（6）：3555－3576.

［37］Zhang T，Bai H F.Analysis of Cable－Stayed Bridge for APDL－Based Optimization［J］.Advanced Materials Research，SAS IP，Inc，2011，243－249：1567－1572.

［38］简金宝，张可村.不等式约束最优化的一个具有强收敛性的强次可行方向法［J］.西安交通大学学报，1999，33（8）：88－92.

［39］杨 俊.基于影响矩阵的大跨桥梁合理成桥状态与施工控制研究［D］.武汉：武汉理工大学，2008：54－55.

［40］唐 密，左德中.综合法初定斜拉桥合理成桥状态［J］.交通科技，2010（2）：30－32.

［41］张文献，刘旭光，李东炜，欧丹.斜拉桥成桥及施工阶段的索力优化［J］.东北大学学报：自然科学版，2009，30（8）：1201－1204.

［42］谢支钢，赵拥军.基于“零位移法＋应力平衡法”确定叠合梁斜拉桥的合理成桥索力［J］.中国市政工程，2012（2）：36－41.

［43］吴轶雄.独塔单索面斜拉桥索力优化研究［D］.大连：大连海事大学，2010：21.

［44］陈素君，张国刚，唐盛华，等.斜拉桥初始平衡构形的确定方法［J］.公路交通科技，2011，28（2）：58－69.

［45］李 文.虚拟温度迭代法在斜拉桥调索计算中的应用［J］.广东公路交通，2012，121（2）：31－34.

［46］Zhang J，Zhong J，He L，et al.An Improved Method of Structural Optimization Based on ANSYS［C］／／2010 Second International Conference on Computer Modeling and Simulation.Ieee，2010：300－306.