改进背景值的新陈代谢GM(1,1)在变形预报中的应用
孙昌瑜,朱军桃
(1.桂林理工大学测绘地理信息学院,广西桂林 541004;2.广西空间信息与测绘重点实验室(桂林理工大学),广西桂林,541004)
改进背景值的新陈代谢GM(1,1)在变形预报中的应用
孙昌瑜1,2∗,朱军桃1,2
(1.桂林理工大学测绘地理信息学院,广西桂林 541004;2.广西空间信息与测绘重点实验室(桂林理工大学),广西桂林,541004)
文献[1]根据GM(1,1)模型的指数特性,通过在其白化微分方程区间上求积分推导出了背景值的一个计算公式。本文在此基础上,利用该公式建立了新陈代谢GM(1,1)模型。实际算例表明由此建立的新陈代谢GM(1,1)模型的预测结果高于传统背景值下的新陈代谢GM(1,1)模型,表明了改进背景值的新陈代谢GM(1,1)模型合理性,其可用于测量数据处理中的变形分析预报。
背景值;GM(1,1)模型;新陈代谢GM(1,1)模型
1 引 言
目前,变形预报的主要方法有回归分析法、确定函数法、时间序列分析法等,但这些方法通常要求有大量样本,而且要求具有典型的概率分布,这在实际生产中有时难以满足,同时也限制了其使用范围。灰色GM (1,1)模型弥补了这一缺陷,但由于GM(1,1)模型随着时间的推移,将会不断地有一些随机扰动或驱动因素进入系统,使前端的数据对末端的数据影响逐渐减弱,导致后期预测误差逐渐增大[2]。很多研究者都在寻找各种方法对GM(1,1)模型进行改进,以提高其预测的精度。例如残差GM(1,1)修正模型[3]以及采用加权,优化等方法[4]以提高模型的精度。虽然这些方法在一定程度上提高了GM(1,1)模型的预测精度,但这些方法较烦琐,没有从根本上对GM(1,1)模型进行改进,不利于实际生产中的应用。基于此,本文在文献[1]的基础上,推导了改进背景值的新陈代谢GM(1,1)模型,并通过工程实例验证了改进模型的可行性和有效性。
2 改进背景值的新陈代谢GM(1,1)模型
2.1 灰色模型背景值的推导[1]
设GM(1,1)模型的原始数据序列为:x(0)(k)= {x(0)(1),x(0)(2),…,x(0)(n)},经过一次累加生成得到的序列为:x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)},

则生成数列x(1)(k)的白化微分方程为:

将上式在[k,k+1]上积分,有:

设背景值Z(1)(k+1)为x(1)(t)在区间[k,k+1]上时,则有:

由此可知背景值即为x(1)(t)在区间[k,k+1]上的定积分。
由于方程(2)的解为指数形式,为方便起见x(1)(t)可用如下指数曲线近似表示:

并假设该曲线过x(1)(k+1)和x(1)(k)两点,因此有:

由式(6)、(7)可得:(1)
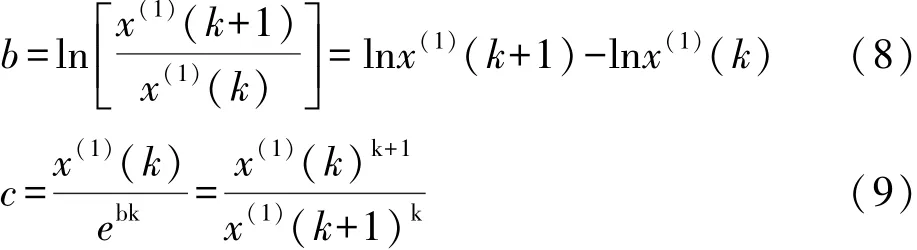
因此背景值为:
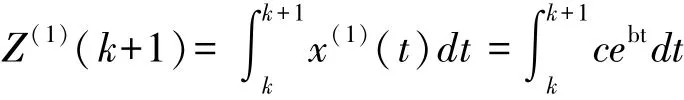
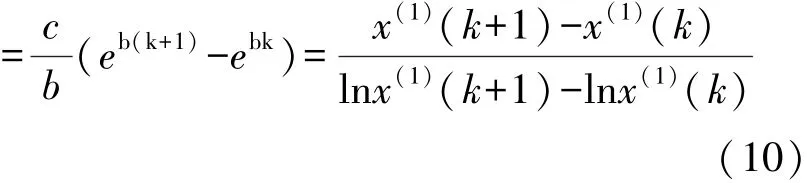


经过一次累减计算(1-IAGO)可以还原出模型的模拟值为:

2.2 改进背景值的新陈代谢GM(1,1)模型原理
在原始数据序列x(0)(k)={x(0)(1),x(0)(2),…,x(0)(n)}中,置入新的数据x(0)(n+1)(该数据是采用GM(1,1)模型依据新的背景值公式(10)式预测一步所得),同时去掉最老信息x(0)(1),用序列{x(0)(2),x(0)(3),…,x(0)(n+1)}作为原始序列,在重复上述步骤建立新背景值得GM(1,1)模型,如此反复依次递补,直到完成预测,此即为改进背景值的新陈代谢GM(1,1)模型。
3 工程实例
西安市南郊某18层建筑物布置了11个沉降监测点,取其中C5、C6点的施工期间13期数据为例进行分析[5]。为了说明本文改进背景值的新陈代谢GM(1,1)模型的预测效果,设计两种方案进行对比分析,其中用前5期数据建立动态模型进行预测,并与其余8期观测值进行比较分析。
从表1分析得出:方案一(传统背景值的新陈代谢GM(1,1)模型)从第10期开始预测残差较大,到第13期时预测残差达到了4.13mm,不利于工程实际的应用。方案二(改进背景值的新陈代谢GM(1,1)模型)与方案1相比,预测精度有了明显的提高,预测的最小残差为0.11mm,最大残差才只有1.7mm。从残差还可得知,方案二明显优于方案一,证明了改进背景值的新陈代谢GM (1,1)模型的可行性,可应用于建筑物的沉降变形预报。

实测值与各模型预测值的比较 表1
为了更直观的说明改进背景值的新陈代谢GM (1,1)模型的优越性,现将C5点各模型的预测值与残差值如图1、图2所示。

图1 沉降值与各模型预测值比较

图2 各模型的预测残差值比较
由图1、图2可以看出:经过改进背景值的新陈代谢GM(1,1)模型的预测值更加接近实测值,其预测效果高于传统背景值的新陈代谢GM(1,1)模型。传统背景值的新陈代谢GM(1,1)模型的预测残差较大,而改进背景值的新陈代谢GM(1,1)模型的预测残差相对较小。因此,改进背景值的新陈代谢模型可以提高预测的稳定度和精度。
由上述可知:改进背景值的新陈代谢GM(1,1)模型的预测结果优于传统背景值的新陈代谢GM(1,1)模型。为了更加充分说明改进背景值的新陈代谢GM(1,1)模型的预测效果,对C6点进行预测,各模型的预测值和残差值如表2所示。

实测值与各模型预测值的比较 表2
由表2可知:传统背景值的新陈代谢GM(1,1)模型从第10期开始预测残差较大,到第13期时预测残差达到了3.5 mm。改进背景值下的新陈代谢GM(1,1)模型预测的最小残差为0.11 mm,而到第13期预测残差才只有1.31 mm。从误差的角度进行分析:传统背景值的新陈代谢GM(1,1)模型预测的最大相对误差为4.49%,而改进背景值下的新陈代谢GM(1,1)模型预测的最大相对误差为1.68%,传统背景值的新陈代谢GM(1,1)模型预测的平均相对误差为1.57%,而改进背景值下的新陈代谢GM(1,1)模型预测的相对误差为0.58%。这更加充分的说明了改进背景值的新陈代谢GM(1,1)模型的可行性和有效性。
4 结 论
在其白化微分方程上求积分推导了背景值的一个计算公式,并利用该公式建立了新陈代谢GM(1,1)模型。通过工程实例表明使用改进背景值的新陈代谢GM(1,1)模型的预测结果明显高于传统背景值的新陈代谢GM(1,1)模型,证明了改进背景值的新陈代谢GM(1,1)模型的合理性,可用于变形监测的分析预报。
[1] 王钟羡,吴春笃.GM(1,1)改进模型及其应用[J].数学的实践与认识,2003,33(9):20~26.
[2] 翟信德,高飞,徐文兵.新陈代谢GM(1,1)模型在建筑物沉降预测中的应用研究[J].城市勘测,2008(3):136~138.
[3] 刘思峰,谢乃明等.灰色系统理论及其应用[M].北京:科学出版社,2008.
[4] 王义闹,刘光珍,刘开第.GM(1,1)的一种逐步优化直接建模方法[J].系统工程理论与实践,2000(9):99~104.
[5] 李日云,王利,张双成.灰色预测模型在高层建筑物沉降预测中的应用研究[J].地球科学与环境学报,2005,27 (1):84~87.
[6] 陈伟清,田海涛,陈佳佳.工程建筑变形分析的灰色模型探讨[J].广西大学学报:自然科学版,2011,36(1):64~70.
[7] 郭峥英,陈鹏宇.建筑地基沉降预测的灰色模型与Asaoka法[J].工程勘察,2012(6):67~70.
[8] 陈伟清.灰色预测在建筑物沉降变形分析中的应用[J].测绘科学,2005,30(5):43~45.
Application Based on Im proved Background Value M etabolic GM(1,1)M odel in Deformation Forecast
Sun Changyu1,2,Zhu Juntao1,2
(1.College of Geomatics and Geoinformation,Guilin University of Technology,Guilin 541004,China;2.Guangxi Key Laboratory of Spatial Information and Geomatics,Guilin 541004,China)
According to the exponential nature of the GM(1,1)model,a background value calculation formula is derived by integrating in albino differential equations interval in references[1].This paper establishesmetabolic GM (1,1)model based on this formula.A practical example demonstrates the metabolic GM(1,1)model thereby established is higher accuracy than the traditional background value GM(1,1)model.It shows that themetabolic GM(1,1) model of improving background value is reasonable and can be used for deformation prediction.
background values;GM(1,1)model;metabolic GM(1,1)model
1672-8262(2013)03-137-03
P258,TU196
A∗
2012—11—28
孙昌瑜(1988—),男,硕士研究生,主要研究方向:变形监测数据处理。
国家自然科学基金(41071294)

