风力发电机载荷连续体结构拓扑优化模型的设计

徐立军，王维庆，程 静

(新疆大学 电气工程学院，新疆 乌鲁木齐 830047)

风力发电机载荷连续体结构拓扑优化模型的设计

徐立军，王维庆，程 静

(新疆大学 电气工程学院，新疆 乌鲁木齐 830047)

讨论了风力机载荷的二维及三维结构的拓扑优化问题。使用拖曳力的规范表达将风载荷引入公式并设计了优化策略，使得在没有阻碍风的模型表面处可以忽略风压。运用带有惩罚因子的各向同性固体材料构建了受到体积约束的最小柔度设计公式，引入移动渐近线法解决了优化问题，并通过线性搜索和改变渐近线的更新公式进行调节。通过施加显示约束控制设计变量的中间密度值得到了黑/白设计。数例验证结果表明，提出的公式合理地将风载荷的影响纳入拓扑优化问题，并通过优化结构中出现的空隙得以体现。

拓扑优化;连续体结构;风载荷;移动渐近线

0 引言

目前，对连续体结构拓扑优化的研究已经相当成熟，各个工程领域的学者们已经在各方面取得了很多创新性成果。很多时候，在不同的研究领域当中，都会遇到载荷对拓扑优化的影响问题，如在静态液压问题中的对结构的流体压力载荷，土木工程结构中的雪荷载以及海岸边沿所受的风力和水力载荷等。在这些问题中，载荷的位置、方向和大小均与具体的结构设计有关，因而不同研究领域的经验有时无法直接进行借鉴。

文献［1］讨论了在静态载荷下弹性连续体结构的拓扑优化问题，该文的作者还引入了一条等距密度曲线以模拟载荷的变化情况。在文献［2］中，进一步使用参数优化的等距密度曲线来代表变化的载荷表面，从而使荷载表面识别模型具有更强的鲁棒性。

在文献［3］中，在保持总载荷恒定的情况下，采用动态线来界定动态载荷。每条动态线的载荷都进行预先定义，将沿该动态线的位置作为优化过程的一部分。通过在流体区域引入低模量材料并加强固体和液体区域之间的平滑移动优化了连续体结构。这一新的结构模式使得液压载荷结构(例如大坝)设计方面的性能有所提高。

文献［4］对依赖于设计载荷制约的拓扑优化问题进行了研究。提出了一种利用虚拟热载荷模拟设计依赖载荷的方法。拓扑优化问题从两相转变为在固体、空隙以及静液压流体最优化分配的设计域中的三相物质分配问题。近来，该文作者又设计了一种新的方法来解决拓扑优化中的载荷问题，即使用混合排驱压力模式来解决基本有限元的问题。

上述文献不能完全适用于本论文提到的风力载荷问题。在本文中，将风力载荷引入二维及三维连续体结构的拓扑优化模式中，将优化问题构建为最小柔度问题，并使用改进的移动渐近法进行分析，根据连续最优化条件对低渐近线进行修改。由于柔度的非单调收敛性，为了确保目标函数的减少并满足限制条件，采用了一维搜索方法并引用了显示函数以获得黑/白设计。

1 标准拓扑优化公式

拓扑优化问题的目标是在一个给定范围内进行最佳的材料分配。在本文中，将普遍使用的最小柔度公式结合材料体积约束提出了拓扑优化问题如式(1):

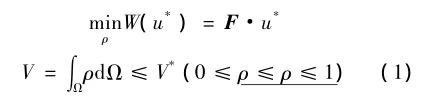
式中:W是结构的柔度，代表外力所做功的大小，也可表示处于平衡状态时的总弹性能;矢量F代表外力;u*是Ω域在平衡状态时的位移场;间断模型中的材料P的密度分配为一个设计变量，小数集P作为P的下界以避免数值不稳定;V*是结构的材料体积V的允许限度。

为获得黑/白拓扑设计，选择著名的各向同性固体微结构(SIMP)方法［5］。材料的刚度定义如式(2):

式中:E0为基础塑性模量;p是惩罚参数［6］(p≥3)。离散结构的局部测量密度指标ρi与有限元网格的结点有关。元素密度¯ρ等于元素周围M个节点的平均柔度插值，其公式为

这种棋盘模式在优化过程中将被自动抑制。

2 风力负载拓扑设计

2.1 风载荷函数

因为风能具有间歇性，随机性的特点，理论上，为了解释作用于某一结构的风载荷的变化，在拓扑优化过程中需要考虑多工况。为简便起见本文只考虑了一种载荷工况;假设风向为从左到右的单方向［7］(见图1a)。

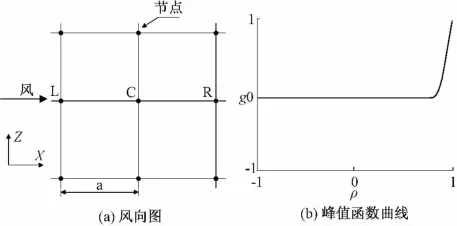
图1 风向和峰值函数曲线图Fig.1 Graph of wind direction and peak function function curve

使用基于直接密度的方法(不考虑载荷受力面的逻辑函数)，将风载荷包括在函数中，通过使用拖曳力标准公式，引入载荷函数g，在离散域的每个节点界定风载荷如式(4):

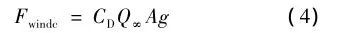
式中:Fwindc是在节点C处的风载荷值;Q∞是来风的动压;CD是阻力系数;A是YZ方面来风作用的侧面区域。A区域的计算取决于C节点位置，即，该节点是在一角、一侧或是该离散区域的中心。例如，对于一个中间节点，在二维情况下，A等于该结构厚度的a倍，而在三维情况下，A等于a2，在本文中，a是均格网格的节点之间的距离。g是峰值函数，其公式为

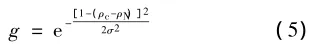
式中:ρc为节点C的密度;ρN为与风向相反的方向上邻近节点的密度;σ为一个标准偏差参数。

风力Fwindc施加于该区域的每个结点处，同时使用峰值函数g将其值导向 0，[ ]1区间(见图1b)，并确保风载荷仅施加于密度发生较大变化的节点处，明确在结构表面载荷是单方向的。也就是说，只有当节点C是在固体区域，以及节点N在空隙时，才施加载荷。

若假设并不存在尾流效应，则该公式特别适用于桁架之类的结构。

2.2 灵敏度分析

设计变量柔度的灵敏度，在这里用节点密度表示［8，9］，其公式为

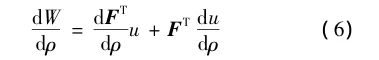
式(6)中的位移的灵敏度可以通过相关结点密度的微分方程得到，并可表示为

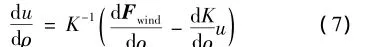
式中:K是全域刚度矩阵;Fwind是风载荷矢量。

柔度的灵敏度可表示为

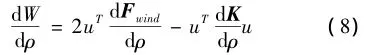
从式(8)中可以看出，柔度的灵敏度受两个因素影响，第一个是由于外力对设计变量的依存度，第二个是由于刚度对同一变量的依存度。分别用ψ和φ来代表这种关系。施加于一个给定结构的外力也可分解为两部分，即静载荷和进风风力。假定恒载与结构外形无关，因此，每个节点C的ψ的表达式只取决于风载荷并简化为

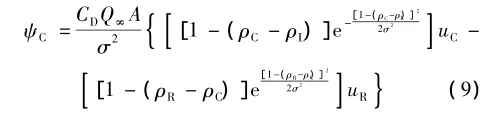
式中:下标L和R分别是指节点C左侧和右侧的节点。采用同样的命名法，uC和uR分别是节点C和其右侧邻近节点的水平位移。

2.3 优化过程

优化问题通过移动渐近法(Method of Moving Asymptotes，MMA)得以解决。柔度的近似公式为

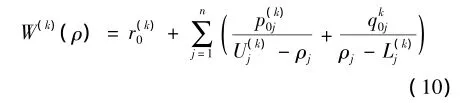
式中:k为MMA迭代指数;n为在离散区节点总数;p(k)0j和qk0j由第一塔克(K－T)条件的一次近似值决定;L(k)j和U(k)j分别是低渐近线和高渐近线。

在某些情况下，当用MMA法求解程序尝试更新渐近线L(k)j和U(k)j时，优化过程易于振动，根据本地K－T条件解释的连续最佳条件，可通过调节低渐近线来稳定收敛性，高渐近线的更新保持不变，使用本地K－T条件连续优化准则进行优化，该函数可近似表示为

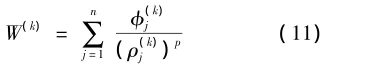
该近似值可通过线性化最近设计点周围的刚度系数ρ(k)j而得到:

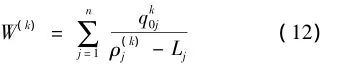
式中:Lj是低渐近线的修正式。

需要注意的是，尽管进行了上述修正，MMA求解程序有时并不收敛，在有些情况下，会发生分叉。为了改善其性能，对系数p(k)0j和qk0j的计算方法，通过分别调节Ф和ψ的灵敏度进行修正:

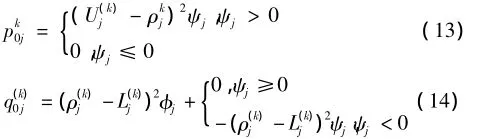
可以看出，在MMA一个步长之后，该目标函数并不总是递减，并且有时会出现违反限制的情况，为了解决这个问题，本文采用了线性搜索，以确保满足限制条件以及目标值的减少。如果kth次迭代之后，MMA计算得出的解用ρ*表示，那么相应的方程:

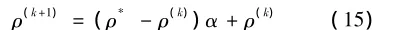
式中:需要计算参数α(α∈［0，1］)，从而满足限制条件和实现目标函数的减少。可使用目标近似三次多项式以及作为自变量α函数的约束来解一维近似最佳化问题，从而得到α的值。

3 显示约束

风力机支撑结构的初步拓扑数据显示如图2(a)所示，为灰度设计，不是预计的黑/白设计。这种结果与如图2(b)所示结点上的风载荷的分布有关。图中的每个方柱是载荷在节点沿着特定垂直线的直方图。需强调的是，风载荷虽然分布在整个定义域，但只在结构底部的少数几个节点处较大，理论上在迎风面的风载荷的分布必须是均匀的，但实际情况并非如此。为了生成黑/白设计，引入显示约束来解决公式化问题，从而控制中间密度。该约束定义为

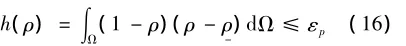
式(16)执行过程如下:在最开始时，该约束条件被忽略，这时显示结果为灰色设计，约束函数的值用ε(0)p表示。然后，问题pk的序列被解出，每个附加约束中的εp是从ε(0)p开始初始化的相关递减序列的第kth项，并根据式(17)进行更新:

该过程一直进行到εp解不收敛为止。

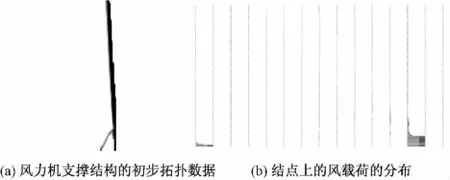
图2 带有显示约束的风机支撑结构拓扑分析结果及风载荷风布图Fig.2 Topology analysis results of wind turbine support structures and the figure of wind load distribution with explicit constraint

4 数值算例

为了评估风载荷对优化拓扑的影响，本文进行了陆地风力机的支撑结构的数值算例。该设计域为如图3所示的平行六面体，在二维情况下，可视为矩形域，轮毂和转子重量为Pwr，以及转子升力Fw视为恒载并施加于该域的顶部中心位置，其值分别为2.55和0.125 MN。该空间域可视为箱形结构，其高度为120 m，长12 m，宽12 m，其底部固定。假定吹来的风是从左向右，风速为25 m/s。在二维和三维情况对该问题进行研究，假设结构为线性变形，使用材料为弹性模量为E=200 000 MPa的钢材，泊松比ν=0.3，惩罚因子设为3，体积比设为0.3，密度采用下限ρ=10－3，峰值函数中2σ2的值固定为0.1，β的值为0.05。

4.1 二维数例

首先进行风机支撑结构的拓扑优化验证。该问题的结果采用一个15*141节点的离散网格生成，如图4所示。图4a和4b分别为无风载荷和有风载荷的分析结果。

图3 设计域图Fig.3 Design domain

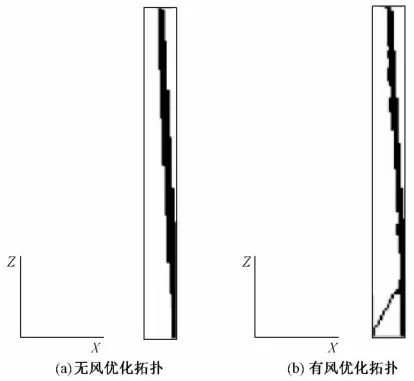
图42D优化拓扑图Fig.4 Optimum 2D topology

可以看出，无风的拓扑是一座只支持恒载的斜塔。而承受风载荷的拓扑在根部有一个枕木。而且，从图4a和4b可看出，该塔是一个有着坚实底座的狭窄的悬臂，产生这种结果归因于两种力量大小的差距:Pwr大约是Fw的20倍。无风载荷的拓扑和有风载荷的拓扑用恒风力载荷计算的柔度分别为0.022 9 MN·m和0.013 9 MN·m。因此，在设计公式中包括风载荷导致同样材料与体积的结构刚度下降了40%。如果力Fw施加于顶面的前端，该塔可能更加倾斜并可能产生更好的优化效果。

图5显示了风机塔架拓扑的演变过程。算法收敛为大约884次迭代的黑/白拓扑。可以看出，该拓扑以灰色列设计开始，以在塔根的枕木的黑/白设计结束。

图6表示，考虑风载荷的设计中的风载荷分布。可以看出，风载荷均匀分布于整个设计域。而在有些情况特别是强风情况下，风力载荷在设计域的某些部分并未均匀分布。这主要是因为柔度近似值的系数的更新方式，以及显示约束参数的减小。需要进行进一步的研究以决定这些系数的合适的更新方案。图6b显示了收敛历史，从图中可以看出，收敛过程相当光滑，在柔度上有一些跳跃，对应于灰度密度的收敛公差。尽管显示约束的引入导致收敛的迭代数量的增加，但得到的解从物理角度上看会更有意义。

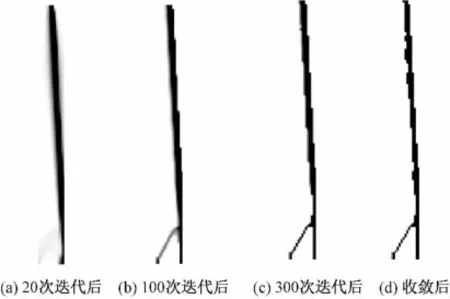
图5 风机塔架拓扑演变过程Fig.5 Evolution of wind turbine tower－truss support topology

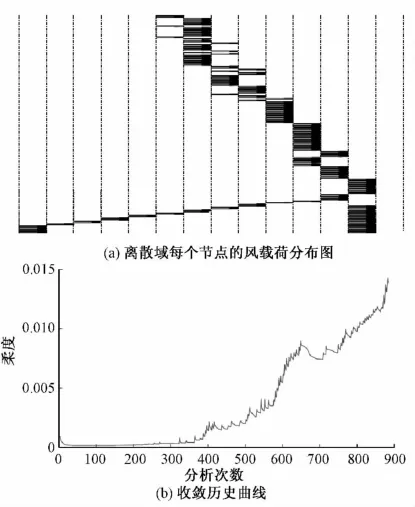
图6 风载荷分布及收敛曲线图Fig.6 Wind load distribution and convergence history curve

4.2 三维数例

陆上风机的域以15×15×141节点呈离散态。图7显示经过后处理为黑/白拓扑结构后，有风载荷和无风载荷情况下，风机优化拓扑的不同表现。没有考虑风载荷的柔度为0.023 9，考虑风载荷的柔度为0.015 1，两个解的差异为37%。

比较图5和图7可以看出，3D拓扑看起来与2D拓扑非常相似。考虑风载荷的风机拓扑由结构底部的两个框架支持。图7表明，在公式中包括风载荷，相比较于没有风载荷的拓扑，面向风力载荷可以有一个较大的空隙。

图7 风机支撑结构的3D拓扑图Fig.7 3D topology of wind turbine support structures

5 结论

本文提出了在最小柔度拓扑优化问题中纳入风载荷的构想。使用该方法无需知道负载表面的明确结构的优点。运用经过修改的MMA方法，并加入了线性搜索以保证拓扑优化问题的收敛，在拓扑优化方程式中加入了显示约束以控制中间密度值，并确保拓扑为黑/白拓扑。用数例验证了风载荷对优化拓扑的影响，分析结果表明，使用该方法进行有风载荷的拓扑结构设计，可以在同样的刚度条件下减小风机的体积，并允许在载荷受力表面有空隙的存在，因此，在初步设计阶段使用该方法，能够显著减少结构重量，从而使得风机制造的总成本降低。

［1］Abdallamm，Gürdalz.Structural design using optimality based cellular automata［C］.Denver，CO:43th AIAA/ASME/AHS/ASC structures，structural dyna，2002.112－118.

［2］Bendsøemp，Kikuchin.Generating optimal topologiesinstruc－tural design using homogenization method［J］.Comput Methods Appl MECH ENG，1988，71:197－224.

［3］Borrvallt，Peterssonj.Topology optimization using regularized intermediate density control［J］.Comput Methods APPL MECH ENG，190:4911－4928.

［4］Chen B－c，Kikuchi N.Topology optimization with design－dependent loads［J］.Finite ELEM ANAL DES，37:57－70.

［5］罗震，陈立平，黄玉盈，等.连续体结构的拓扑优化设计 ［J］.力学进展，2004，34(4):463－476.

［6］崔海涛，桑韧，温卫.应力和位移约束下连续体结构的拓扑优化 ［J］.航空学报，2005，26(1):54－57.

［7］宋宗凤，陈建军，朱增青.应变能约束下多随机参数连续体结构的拓扑优化［J］.西安电子科技大学学报 (自然科学版)，2009，36(6):1079－1085.

［8］隋允康，边炳.屈曲与应力约束下连续体结构的拓扑优化 ［J］.工程力学，2008，25(8):6－12.

［9］叶红玲，隋允康.应力约束下连续体结构的拓扑优化［J］.北京工业大学学报，2006，32(4):301－305.

Wind load modeling for topology optimization of continuum structures

XU Li－jun，WANG Wei－qing，CHENG Jing
(College of Electric Engineering，Xinjiang University，Urmqi 830047，China)

Topology optimization of two and three dimensional structures subject to wind loading is discussed.The wind loading is introduced into the formulation by using standard expressions for the drag force，and a strategy is devised so that wind pressure can be ignored where there is no surface obstructing the wind.A minimum compliance design formulation is constructed that subject to a volume constraint using a solid isotropic material with penalization model.The optimization problem is solved using the method of moving asymptotes，modified by including a line search and by changing the formula for the update of asymptotes.To obtain the black and white design，intermediate density values，which are used as design variables，are controlled by imposing and explicit constraint.Numerical examples of a windmill structure show that the proposed formulation rationally incorporates the effect of wind loading into the topology optimization problem as illustrated by void appearing in the optimal structure.

topology optimization;continuum structure;wind loads;moving asymptotes

TM315

A

1007－2691(2013)05－0015－05

10.3969/j.ISSN.1007－2691.2013.05.03

2013－06－01.

国家自然科学基金资助项目 (51267017).

book=30,ebook=6

徐立军 (1978－)，男，副教授，研究方向为风力发电机控制及其并网。