支挡结构中锚杆(锚索)极限抗拔力研究

蒋宏为

(1中国人民解放军后勤工程学院军事土木工程系，重庆400016；2重庆建工集团，重庆401122）

支挡结构中锚杆(锚索)极限抗拔力研究

蒋宏为1，2

(1中国人民解放军后勤工程学院军事土木工程系，重庆400016；2重庆建工集团，重庆401122）

该文以支挡结构中锚杆(锚索)为研究对象，介绍了现有锚杆(锚索)抗拔承载力计算方法，分析了统一强度理论的锚杆(锚索)极限抗拔力计算方法，并作了在实际工程中应用算例的分析，进一步明确了影响支挡结构中锚杆(锚索)极限抗拔力的因素及力学状态，为支挡结构在工程建设中的设计与施工提供参考。

支挡结构；锚杆（锚索）；极限抗拔力；岩土结构形式；抗拔承载力；摩擦力；统一强度理论；抗剪强度

0 引言

在工程建设中，无论是房屋建筑工程、市政工程还是公路工程，在地形条件受限或者需要保护建构筑物时往往采用垂直支挡结构，在这种结构的应用过程中，其中锚杆(锚索)的极限抗拔力为该结构设计和施工的控制因素。

当锚杆（锚索）在发生作用的过程中，锚杆（锚索）由于疲劳或者拉力过大造成锚杆（锚索）材料产生极限应变，此时产生的内力为锚杆(锚索)的极限抗拔力。通常条件下，锚杆嵌入岩体部分与岩体之间的摩擦力、锚杆与灌入孔道的砂浆之间的握裹力、锚杆自身的强度刚度和稳定性为锚杆（锚索）极限抗拔力的主要控制因素。在设计中，主要考虑的因素为工程所在地自身特点、岩土结构形式、工程造价、施工条件等。

一般来说，预应力锚杆（锚索）的工作机理为：锚杆为传力装置，传递来自锚杆端头和嵌入岩体部分的力，锚杆与灌入砂浆与岩体的摩擦力控制了岩土体的稳定性。

1 抗拔承载力计算方法

在支挡结构整体保持稳定性情况下，支挡结构中的锚杆（锚索）结构同样需要保证不被破坏。此时，灌入孔洞的砂浆和锚杆（锚索)的相互作用力与锚杆（锚索）和岩土体之间的摩擦力构成了锚杆（锚索）的抗拔承载力。以下主要对这两方面做较深入的研究。

1.1 水泥砂浆与锚杆(锚索)的作用力计算方法

由锚杆(锚索)嵌入岩体部分水泥砂浆与锚杆（锚索）的相互作用力得到锚杆（锚索）极限抗拔承载力P1为:

其中 ξ——锚杆（锚索）数量在两根以上时的接触面粘结强度降低系数，一般取值为0.55～0.75；

N——锚杆（锚索）根数；

D——每一根锚杆（锚索）直径（m）；

La——嵌入岩体段长度（m）；

qc——水泥砂浆与锚杆（锚索）之间作用力，根据现场试验或查阅相关规范得到。

1.2 嵌入岩体部分和锚杆（锚索）摩擦力计算方法

锚杆(锚索)嵌入岩体部分在不同的岩体条件下所产生的摩擦力是不一样的，同时与锚杆（锚索）的形状有关，比较常用的是V字型和圆柱型两种形式。以下分别介绍了两种不同类型锚杆的极限抗拔力计算方法。

(1)V字型锚杆（锚索）

其中L1、L2——锚杆（锚索）嵌入岩体段不同杆体直径段的长度(即L1+L2=La)；

D——杆体端头较小直径；

qs——锚杆（锚索）嵌入段与四周岩土体之间的结合强度，该数值一般根据类似工程项目确定；

D1——杆体端头较大段直径；

cu——岩土体不排水抗剪强度值，一般由土工试验确定；

βc——直径较大段锚杆（锚索）抗拔力系数，一般根据现

场实测与相关实际工程确定[1]。

(2)圆柱型锚杆（锚索）

砂性土：P2=πD(qs+σtanδ)1-2

粘性土：P2=πDLaqs1-3

其中D——每一根锚杆（锚索）直径；

δ——嵌入岩体段与四周岩土体之间的摩擦角；

σ——斜坡整体破坏面的法向应力，影响其大小的因素为岩土体厚度和孔道内混凝土强度。其他符号意义同前文。

在实际工程项目中，锚杆（锚索）抗拔承载力取用上述两种方法计算得到的结果的较小值，即P=min(P1，P2)。

2 统一强度理论锚杆(锚索)极限抗拔计算方法

2.1 统一强度准则与抗剪强度

材料抗剪强度理论在20世纪50年代开始由单一剪切面问题的研究转向双剪应力强度理论，并在60年代取得了突破性的进展。该理论以双剪单元体为研究对象，撇开单元体的大小主应力，把单元体中主应力做为材料破坏时的决定因素，建立中主应力统一强度理论。由此填补了莫尔一库伦强度理论经考虑大小主应力的缺点。在岩土工程学中，单元体受到压应力为正，受到拉应力为负。那么，统一强度理论计算公式为[2]:其中b——中主剪应力大小相关系数；σt——材料拉伸强度值；

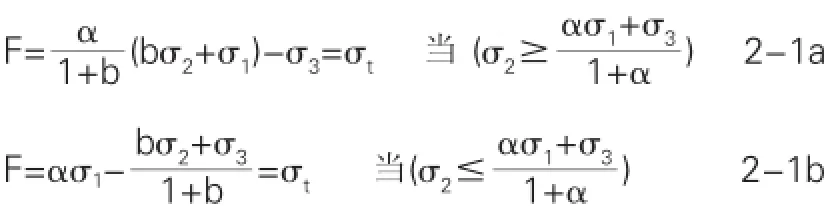
α——材料拉应力与压应力之比。岩土工程中材料参数c0、φ0和α、σt在数量上的关系可以表示为：

将2-2和2-3代入2-1中可以得到统一强度理论的抗剪强度表达式为：

其中，σ——材料剪切面上的正应力。

2.2 锚杆(锚索)所在结构破裂面形态与破坏模式

通过工程实践中已经积累了关于锚杆(锚索)所在结构面形态和破坏模式主要有以下四种模式[3]：

(1)锚杆（锚索）拉断破坏。当锚杆（锚索）嵌入岩土体较深时，锚杆（锚索）与岩体之间有较强的结合力，当外力过大时，锚杆（锚索）材料将发生拉断破坏。

(2)V字形破坏。当锚杆（锚索）嵌入岩土体较浅时，锚杆（锚索）与岩土体结合部发生呈“V”字形的碎裂破坏。

(3)滑动破坏。当锚杆（锚索）嵌入岩土体段与灌入的水泥砂浆作用力较弱时，在外力作用下，锚杆（锚索）很轻易的从灌浆孔道中脱落并滑动，造成结构失稳破坏。

(4)整体破坏。目前锚杆（锚索）结构破坏并不是单一的某一方面的材料或结构的强度、承载力不足造成的，而是结构在长期受到外力作用下，首先是岩体表面开始碎裂，裂缝随之发展，沿灌浆孔道延伸，最后锚杆（锚索）整体从孔道中滑动出来，结构破坏。

2.3 锚杆(锚索)极限抗拔力计算方法

前文对锚杆（锚索）所在结构面的破坏形态和破坏模式做了分析，得到锚杆（锚索）结构整体破坏最为常见。那么，本文以锚杆（锚索）整体破坏模式为研究对象计算极限抗拔力。通过分析，在该种破坏模式下，锚杆（锚索）的极限抗拔力由以下两方面构成：一方面为灌浆孔道内水泥砂浆体所受到的拉力；另一方面为锚杆（锚索）嵌入岩土体部分与灌浆孔道之间的摩擦力[4]。

2.3.1 水泥砂浆体拉力计算分析

图1为锚杆（锚索）与支挡结构中的位置关系，其中S为锚杆（锚索）在结构物表面距结构物顶端的距离；β为锚杆（锚索）在岩土体中的倾斜角度；L为锚杆（锚索）锚固段的长度值；h为锚杆（锚索）在岩土体中自由段的长度值。以锚固段端部结构体为研究对象，如图1右下方图示所示。建立以Z轴为锚杆（锚索）在岩土体中的中轴线方向，X轴方向为其法线方向的计算模型进行分析。

图1 锚杆（锚索）在支挡结构中的相对位置图

假定图1中锚固段界面及其下部岩土体的平均容重为γ’，界面以上所有岩土体的容重为γ，岩土体的侧向土压力系数

为ko，则得到Z轴上某一点的垂直应力和法向应力q1、q2计算公式：

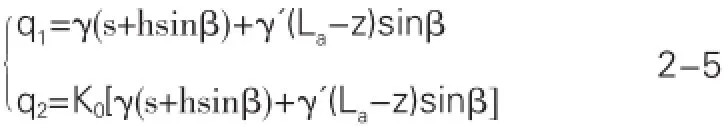
在此基础上，结合极限平衡准则与前面介绍的统一强度准则为基本原理研究锚杆（锚索）在结构破裂面上的平衡受力状态，以此来计算锚杆（锚索）的极限抗拔力。

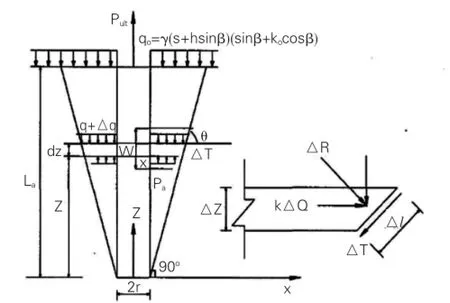
图2 极限抗拔力计算模型图

假定锚杆（锚索）嵌入段界面上岩土体的作用可以简化为均布荷载[5]作用，具体计算公式为：q0=γ(s+hsinβ)(sinβ+ K0cosβ)，如图2为简化计算时某一单元体在平衡状态下的受力图示，图中τ*为单元体破裂面上的切向应力，σ*为单元体破裂面上法向应力，△L为破裂面的长度值，则σ*在单元体处于平衡条件时的表达式为：

σ*=[γ(s+hsinβ)+γ'(L-z)sinβ][sinβ+K0cosφ0)cosθ+ (cosβ+K0sinβ)sinθ]2-6

其中θ——单元体破裂面与X轴方向的夹角。则通过理论力学中平衡原理得到:

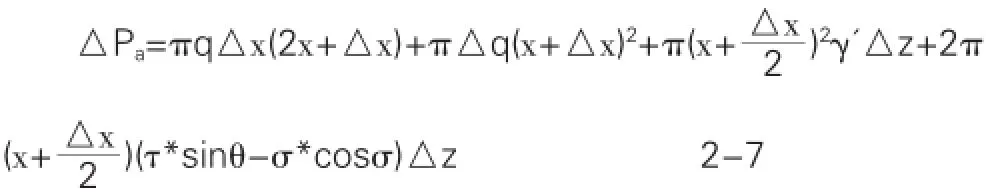
省略公式2-7中微分的高阶项并对等式两边分别取极限，得到:

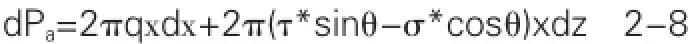
其中

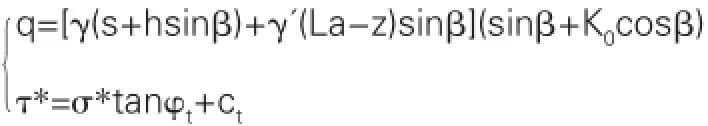
根据统一强度准则，则公式2-8可以简化为:

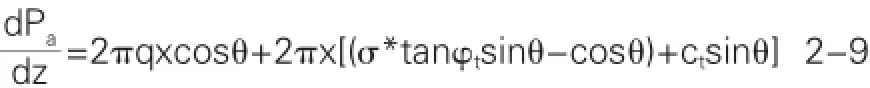
对公式2-8式进行定积分计算，可得出锚杆（锚索）水泥砂浆体拉力的极限拉力计算公式为:

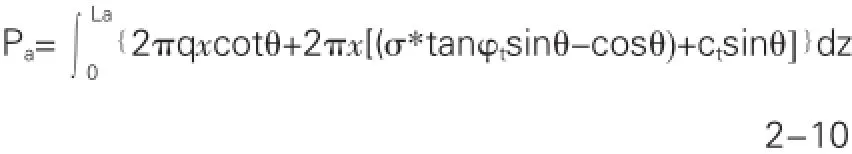
2.3.2 孔道摩擦力计算分析

当锚杆（锚索）孔道内水泥砂浆在外力作用下破碎，锚杆（锚索）整体从灌浆孔道内滑动。此时结构的破坏面为锚杆（锚索）与周围岩土体的接触面则该条件下的极限抗拔力计算公式为：

其中τ*'=σ*'tanφ't+c't，φ't，c't锚杆（锚索）结构和周围岩土体接触时的界面力学参数，σ*'——围岩压力，根据岩体力学可以得到其计算式为:

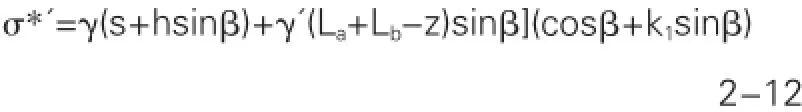
其中，La+Lb=L，k1——在施工过程中孔道灌浆时对孔道壁的压力系数。

2.3.3 极限抗拔力计算公式

综合前文对锚杆（锚索）的极限抗拔力计算分析，将极限抗拔力的两部分相加可以得到以下计算公式:

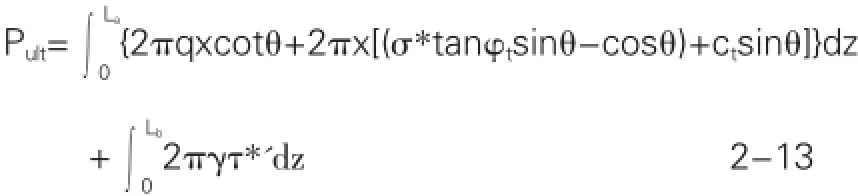
在实际工程运用中，应在准确掌握工程所在地岩土体的力学性质和具体参数的情况下确定相关计算参数，然后利用数值计算方法进行数值求解计算，得到满足工程实际需要的结果。

3 算例分析

通过以重庆某处间建筑边坡为实体案例，该边坡表层覆盖层较厚，局部有基岩零星出露，上覆土层为第四系残破积碎石土，其中含部分块石，碎石土厚约为14.2m，结构松散，稍湿，力学性质差。出露基岩为志留系徐家坝组(S2xj)页岩，基岩强风化层厚2.8～5.2m，为极软岩；基岩中风化岩体较完整，为软岩。

在现场施工开挖过程中，通过对垂直支挡结构中某一组锚索进行了试验分析，所有锚索倾斜角均为17°，嵌入岩土体段锚索长度为6.5m，未嵌入段长度为4.5m，接近边坡表面的岩土体厚度为4.5m，锚孔道直径为150mm，灌浆压力为0.65MPa。锚索未嵌入岩体部分的岩土体的平均重度γ1=20.5kN/m，嵌入部分岩土体的力学计算参数为:γ2=24.5kN/m，φ=41°，

c=276kPa，通过试验得到锚索的界面参数为:φ=43°，c=

211kPa。水泥砂浆段的侧压力系数k0为0.55，岩土体的侧压力系数k1为1.7。计算结果如表1所示。

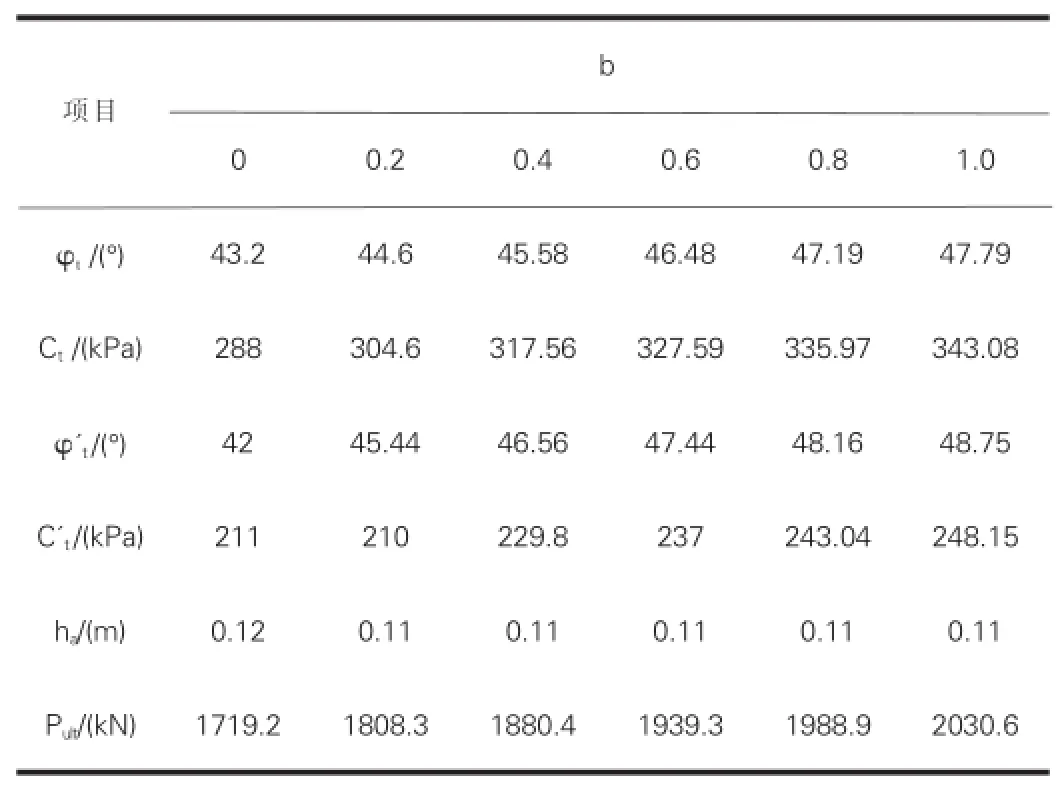
表1 不同条件下锚索极限抗拔力计算结果

通过实际工程中对极限抗拔力计算结果分析可以得到（如表2），在岩石结构中锚索的极限抗拔力随破裂体的高度变化而变化。在不同的岩体结构中，中主应力对极限抗拔力的作用规律是一样的，是一个比较稳定的值，其中锚索的极限抗拔力大小受控于锚索和水泥砂浆体的粘结强度。

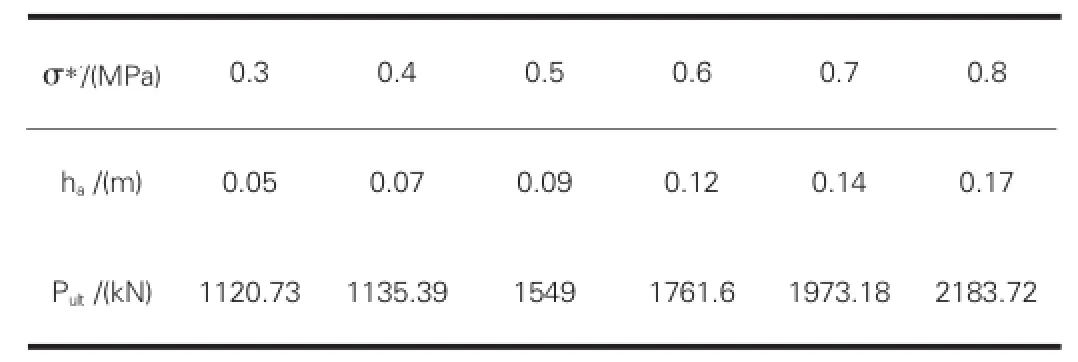
表2 围岩压力对极限杭拔力和锥体高度的影响

同时可以推出，伴随着围岩压力的增加，极限抗拔力与破裂体高度的增加呈线性递增趋势，说明围岩压力也是主要控制极限抗拔力主要因素。

4 结论

通过对垂直支挡结构中锚杆(锚索)极限抗拔力的计算分析，可以得出以下结论:

（1）统一强度准则在计算锚杆（锚索）极限抗拔力时，比较全面地考虑了支挡结构中锚杆（锚索）在极限破坏时的各种因素，比如锚杆（锚索）破裂面形态、锚杆（锚索）在岩土体中的倾斜角度和围岩压力等。

（2)通过实际工程案列的计算分析，可知随着中主应力系数值的增加，锚杆（锚索）的极限抗拔力随之递增，此时对水泥砂浆体的高度并没有影响。

（3)影响锚杆（锚索）的极限抗拔力大小的因素主要嵌入段岩土体与锚杆（锚索）材料的摩擦力、锚杆（锚索）与水泥砂浆体的作用等。

[1]陈祖煜,杨健.岩土预应力锚固技术的进展[J].贵州水力发电,2004,28(5):5-10.

[2]华东水利学院.土工原理及计算[M].北京:水利电力出版社,1982.

[3]唐保付.二次高压灌浆提高土锚承法力机理研究[D],岩土锚固新技术论文集,北京:人民交通出版社,1998.

[4]刘小丽,周德培,杨涛,等.预应力锚索抗滑桩设计中确定锚索预应力值的一种方法[J].工程地质学报,2002,10（3）:317-320.

[5]吴金生,吴和政,王全成,等.框格梁式预应力锚索在公路滑坡治理中的应用[J].中国地质灾害与防治学报,1998,9:308-312.

责任编辑：孙苏，李红

施工经验

加气块填充墙抹灰应采取什么措施

在粉煤灰蒸压加气混凝土砌块填充墙上进行抹灰后，常出现墙面抹灰层空鼓和表面裂缝现象，这是建筑工程质量通病之一。解决这个问题，应该从减少墙体的收缩和增强墙体与抹灰层之间的粘结力着手。为此，建议采取以下一些措施。

1.加气混凝土砌块砌筑时，其龄期至少应在28d以上，这样可减小砌块的收缩值。

2.抹灰前，墙面应清扫干净，然后浇水湿润。由于加气混凝土材料毛细管为封闭性和半封闭性，故吸水速度大大低于砖砌体，因此，应提前2d浇水，每天浇两遍以上，这样可使墙面在抹灰时处于湿润状态，有利于抹灰层与墙体的黏结。

3.抹灰应分层进行，一般每次抹灰厚度应控制在10mm左右，待前一层抹灰七八成干后，再抹下一层。

4.与柱和顶板交接处，必要时可加设钢丝网或拉结筋。（摘自：《建筑工人》）（敬请作者速与本刊编辑部联系，以便付酬）

Study on Ultimate Pullout Force of Bolt（Anchor）in Retaining Structure

Based on bolt(anchor)in retaining structure,the calculation method of its anti-pull force is introduced,the calculation method of its ultimate pullout force is analyzed with unified strength theory and practical engineerings are taken as examples.Factors and mechanical state influencing bolt(anchor)ultimate pullout force are further specified.It offers some

for future engineering.

retaining structure;bolt(anchor);ultimate pullout force;geotechnical structure form;anti-pull force;friction force;unified strength theory;shear strength

U416.1+4

A

1671-9107（2013）08-0036-04

2013-06-03

蒋宏为（1986-），男，重庆人，硕士研究生，助理工程师，研究方向为路桥施工技术，从事路桥施工技术管理工作。

10.3969／j.issn.1671-9107.2013.08.036