不确定条件下的闭环供应链网络优化

孙玲芳，廖承承

(江苏科技大学经济管理学院，江苏镇江212003)

如今闭环供应链受到越来越多的关注，整合正逆向供应链，构建高效的闭环供应链系统，是企业供应链战略层规划的关键问题.其中闭环供应链的网络构建和优化是当今中外学者关注的热点之一.文献［1］中对退货的多级逆向物流网络进行了研究;文献［2］中构建了一个多级多产品的再造逆向物流网络模型;文献［3］中研究了环境和参数不确定性条件下的闭环供应链设计问题.国内，文献［4］中研究了设施能力有限和顾客需求确定条件下的逆向物流网络设计;文献［5］中建立了一个同时考虑修理和再制造两种回收再利用方式的逆向物流网络设计模型，但没有考虑不确定性的影响;文献［6］中研究了需求量、可回收量和最小回收率确定条件下的制造/再制造集成物流网络设施选址问题;文献［7］中在制造/再制造集成物流网络中考虑了回收产品的数量及质量的不确定性;文献［8］中在单周期闭环供应链网络选址模型中考虑了产品需求量确定而废弃产品回收量不确定的情况;文献［9］中分析了废旧产品回收过程中的存在的产品返回时间和数量、零件拆卸以及可再制造率不确定性，并建立了相应的预测模型;文献［10］中建立了随机需求情形下的均衡约束的设施竞争选址模型.

尽管目前学者对闭环供应链网络构建或设计有所研究，考虑不确定因素的研究也不少，但在综合考虑多种不确定因素条件下闭环供应链网络构建的研究却不多，而现实中存在大量错综复杂的不确定因素，因此采用一定的优化方法对多种不确定条件下的闭环供应链网络构建具有一定的研究意义.基于此，文中的主要目的是在考虑市场需求，回收产品的质量和回收量以及回收产品的再制造成本不确定条件下，运用鲁棒优化方法对闭环供应链的网络构建进行研究，确定各种设施的数量和位置，并对各设施间的物流量进行合理分配.

1 问题描述

考虑制造商自建一个再制造闭环供应链网络.在该网络中，消费市场已知，工厂、分销中心、回收中心及回收点等设施需进行新的选址定位，在各备选地点选择.工厂不仅负责新产品的生产，同时还对回收产品进行再制造，以满足消费区域对其产品的需求量.分销中心的主要功能是存储来自工厂的产品，并将其分销到各消费区域.在没有被选为回收中心的消费区域建立回收点，负责回收来自消费区域的废旧产品，并将其运送至回收中心.回收中心兼有回收点的功能，同时，回收中心要对回收点运送过来的废旧产品进行检测、分类等操作(统称为分拣)，然后将适合回收再制造或再利用的产品或零部件运送至工厂，而对不能进行再利用或再制造的产品或零部件运送至已知的废弃点进行废弃处理(填埋或再生等).

文中的目标是使总费用(包括新设施的建设费用、运输费，回收产品的回收费用和分拣费用，新产品生产费用和回收产品的再制造费用，为满足消费区域需求的违约费用)最小化，同时要确定各设施的数量和位置，并对构成此闭环供应链路径上的各种物流量进行合理分配.

2 基本模型

文中作以下几点假设:①为方便模型的构建，假设回收中心对废旧产品进行分拣后有固定的废弃率，剩下的可再利用或再制造的产品或零部件所拥有的各个零部件数量刚好等于制造若干个再制造产品n所需要的各个零部件的数量，而不考虑任何有效零部件的多余或缺失;② 工厂同时进行两种新产品的制造和回收产品的再制造;③消费区域对某种产品的回收量不得大于该种产品的销售量，各种产品都有回收率(为回收量占销售量的比例);④回收产品的质量由回收中心对回收产品的废弃量来表示;⑤消费市场和废弃产品的填埋点已知，不考虑废弃产品的运输费用和处理费用.

2.1 符号与参数

模型中符号与参数说明:i，j分别表示工厂地点、备选分销中心地点，i∈{1，2，…，I}，j∈{1，2，…，J};k，l，r表示已知的消费区域，k，l，r∈{1，2，…，K};n 表示产品种类，n∈{1，2，…，N}cj分别表示开设工厂、回收中心、回收点和分销中心的固定建设成本表示由工厂i运往备选分销中心j的第n种产品的单位运费，这些产品包括新产品和回收后再制造的产品表示由备选分销中心j运往消费区域k的第n种产品的单位运费;表示由消费区域k运往回收中心l的第n种废旧产品的单位运费，包括废旧产品由回收点k运往回收中心l的情况和回收中心l回收废旧产品的情况表示回收中心l对第n种废旧产品的单位分拣成本表示由备选回收中心l运往工厂i的第n种废旧产品的单位运费;表示消费区域对第n种废旧产品的单位回收成本表示工厂i生产第n种单位再制造产品所需生产成本;表示工厂i生产第n种单位新产品的生产成本表示运往消费区域k的第n种产品的数量未满足消费区域k对第n种产品需求量的单位违约成本;ykn表示消费区域k对第n种产品的回收率;βln表示备选回收中心l对第n种废旧产品进行分拣后的废弃率;表示运往工厂i的第n种回收产品的再制造率分别表示工厂、备选分销中心、备选回收中心对第n种产品的最大处理能力分别表示工厂、分销中心、回收中心建设的最大数量限制．

2.2 基本模型

利用上面的符号，可以将模型写成如下形式:

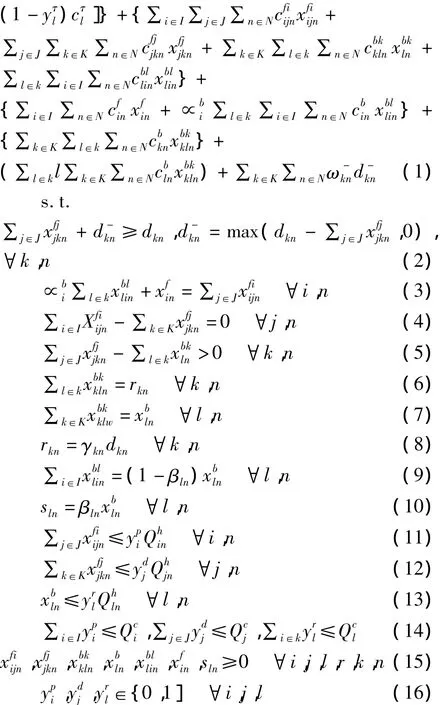
模型中，式(1)为目标函数，它由设施建设成本、运输成本、新产品和再制造产品的生产成本、废旧产品的回收成本、废旧产品的分拣成本以及未满足消费市场需求的惩罚成本构成;式(2)考虑了消费市场上产品的所有需求，包括满足的需求和未满足的需求;式(3)是工厂的流量平衡约束;式(4)是分销中心的流量平衡约束;式(5)考虑了消费市场上的废旧产品不可能全部回收;式(6)是初始回收点流量平衡约束;式(7)保证了每个回收中心总的回收量等于各个回收点流向该回收中心的数量之和;式(8)是废旧产品回收量与市场需求之间的关系;式(9，10)是回收中心的流量平衡约束;式(11～13)分别保证了工厂、分销中心和回收中心的对产品的处理量不得超过各自的处理能力或容量限制;式(14)对各设施的建设数量进行了限制;式(15)是对决策变量的非零约束;式(16)是决策变量的0-1约束.至此，建立了一个确定性的优化模型，在此基础上，运用鲁棒优化方法，建立鲁棒优化模型.

3 鲁棒优化模型

线性规划模型的一般形式如下:

c，d，A，b是定义模型输入的参数.假设参数受不确定性影响，给定不确定性集合U:

文献［11］将式(17，18)构成的模型的鲁棒对应定义如下:

作为一个半定线性优化模型，模型(19)很难求解，但在紧凸不确定集下的鲁棒对应则是容易求解的数学凸规划问题［12］.为了便于模型的优化和求解，首先将式(1～16)按照式(17～19)的形式转换成如下模型:

在模型中，z为目标函数;变量 f，c，d，r和s分别代表固定建设成本、回收产品的单位再制造成本、消费区域的市场需求、消费区域的回收量和回收中心的废弃量;y，x分别为选址的二元变量、再制造产品的决策变量;q表示设施选址的数量约束;矩阵 B，E，H，K，P，V，W 则是控制变量的约束矩阵;其中，c，d，r，s为不确定因素.根据上述鲁棒优化方法，这些不确定参数可以描述成一个有界闭空间UBox:是n维变量ξm的名义值，Gm代表不确定度量的标尺，常令，ρ为不确定水平的参数，代表不确定性大小的稳定程度.当ρ=0时是确定的，随着ρ的增大，不确定性增加.

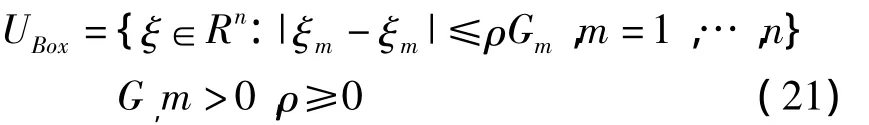
因此，上述不确定因素可以描述成以下有界闭空间:

对约束式 fy+cx≤z，有

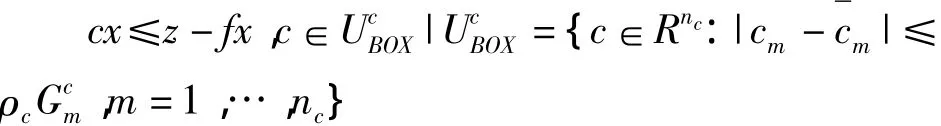
不等式左边包括所有不确定性参数，右边包括全部的确定性参数.进一步变形为

引入新的决策变量tm，得到为简便起见，令，则

同理，对约束式有ax≥d，有

变形成如下形式:同理，对其他约束式可以变形为:

因此，基本的鲁棒对应模型如下:

min fy+cx;

s.t.式(23～26)，Bx=0，Hx≥0，Px≤Vy，Wy≤q，y∈{0，1}，x，η∈R+.考虑模型中不确定性因素，根据上述鲁棒对应模型，建立闭环供应链网络鲁棒优化模型:

其他约束式同式(3～5，7～9，11～14，16).

至此，建立了闭环供应链的鲁棒优化模型.

4 算例分析

构建一个闭环供应链网络，已知有6个既定的消费区域，现考虑在这6个消费区域建立若干个回收中心，在没有建立回收中心的消费区域建立回收点，备选工厂和分销中心地点都是4个，假设在该闭环供应链网络中只生产并回收2种产品.要求工厂、回收中心和分销中心的选址数量上限分别为3，3，4.模型已知的参数如表 1.

1)计算结果

根据上述数据，文中采用lingo9.0软件包进行求解.首先，在确定性条件下，对目标函数值进行最优化，当ρc=ρd=ρr=ρs=0时，目标函数的最优解为z=4 176 034，其他决策变量的最优解如表2～6.

根据计算结果，在确定性条件下，在备选工厂地点1建立工厂，在备选分销中心2，4建立分销中心，在消费区域6建立回收中心，其他消费区域建立回收点.

表1 模型已知参数表Table 1 Parameters known in the model

表2 确定模型的选址决策Table 2 Location decisions of deterministic model

?

表4 工厂到分销中心的物流量的分配Table 4 Amount of logistics of products from plants to distribution centers

表4 工厂到分销中心的物流量的分配Table 4 Amount of logistics of products from plants to distribution centers

xfi 121 xfi122 xfi141 xfi142其他800 930 1 730 1 650 0

表5 分销中心到消费区域的物流量的分配Table 5 Amount of logistics of products from distribution centers to customer zones

表5 分销中心到消费区域的物流量的分配Table 5 Amount of logistics of products from distribution centers to customer zones

?

表6 回收点到回收中心的物流量的分配Table 6 Amount of logistics of recycled products from collection points to recycling centers

表6 回收点到回收中心的物流量的分配Table 6 Amount of logistics of recycled products from collection points to recycling centers

?

接着考虑在不确定性条件下对目标函数值进行最优化，当ρc=ρd= ρr= ρs=0.2，0.5，0.8，1 时目标函数值如表7.

表7 各个不确定条件下的最优目标函数值和选址决策Table 7 Optimal objective function values and location decisions under uncertainties

表7显示在不同的ρ值(不确定性水平)下，各个物流设施点的选址发生了变化.在不确定水平较小(ρ=0.2)的情况下，为尽量减小系统的总成本，满足最大的市场需求，工厂选择了容量最大的工厂地点4作为最终的生产厂址;随着不确定性的增加，生产逐渐扩大规模(工厂选址改变为工厂地点1和3，扩大了总的生产规模，分销中心和回收中心也相应扩大)，以应对来自各种不确定因素的风险;当不确定水平达到一个较高水平时(ρ=0.8和ρ=1)，在生产能力仍能满足市场需求条件下，分销中心扩大了规模和网点，分散应对各消费市场需求不确定性的风险，而此时可以再造的回收产品量也出现了较大波动，此时，系统需要更为分散的网络结构，这就是为什么此时回收中心的规模和网点逐渐缩小(ρ=0.8时回收中心收缩为地点2和6)甚至不再设网点(ρ=1时，回收中心选址地点为0)而直接在消费市场设置成本更为低廉和网点更为分散的回收点.同时，表7也表明随着不确定性的增加，物流网络的总成本也随着增加，鲁棒优化是在考虑最坏情况下系统的总成本最小，所以随着不确定性的增加，在尽量满足各种需求和不确定性的条件下，总成本也会相应增加.

2)参数敏感性分析

闭环供应链的网络构建受到多种不确定性因素的影响，这些不确定性因素对系统具有潜在的影响力，因此找出哪种不确定性因素对系统产生关键性的影响是十分重要的.文中以系统的总成本z为目标函数，通过分别测算回收产品的单位再制造成本、产品的市场需求、废旧产品的回收量以及回收中心对回收产品的废弃量的变动对系统总成本的影响大小，来分析不确定性因素对系统的敏感程度，各个不确定因素的变动大小则通过不确定水平值 ρc，ρd，ρr，ρs的变动来分别加以描述.

表8为各个不确定水平值分别变动而其他不确定水平值为0(即为确定的)时系统总成本的大小.图1反映了表8的目标函数值z的变动趋势.

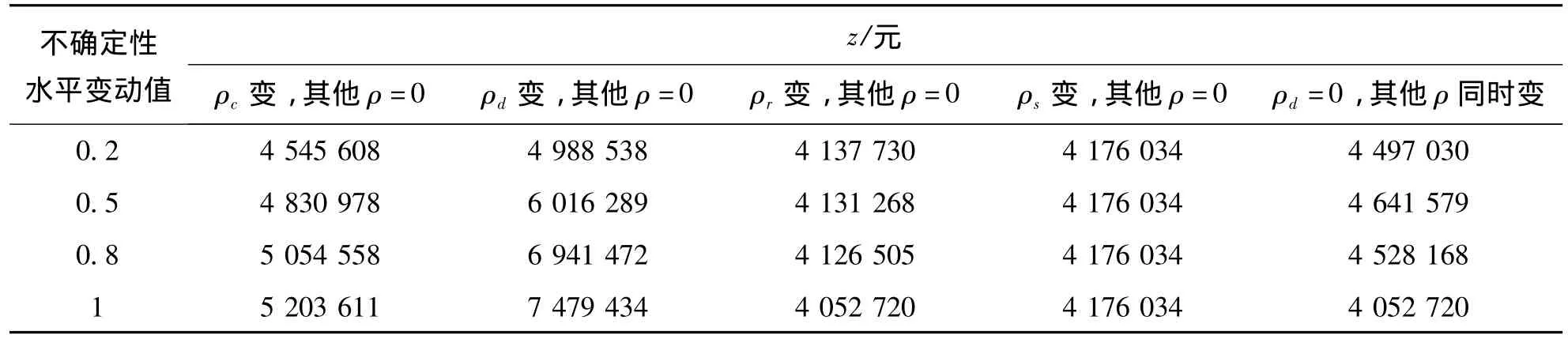
表8 各个不确定性水平值变动时的目标函数值表Table 8 Table of objective function values under uncertainties

图1 各个不确定性水平值变动时目标函数值Fig.1 Objective function values under uncertainties

从图1中可以看出，在其他ρ=0的条件下，市场需求不确定对系统的目标总成本产生更为显著的影响，其次是回收产品的单位再制造成本，而废旧产品的回收量和回收中心对废旧产品的废弃量对系统的目标总成本影响很小.因此，可以初步确定，市场需求是影响系统的目标总成本最为敏感的因素，其次是回收产品的单位再制造成本.为了进一步考察这两个因素对系统的总目标成本的影响，图中还给出了另外几种情况的总成本走势线.当所有的ρ都同时变动时，目标函数值随着不确定水平的升高而快速增长;当ρd变动，其他ρ=0时，目标函数值也是随着不确定水平的升高而快速增长，其增长幅度仅次于“所有的ρ都同时变动”时的增长量;当ρd=0，其他ρ同时变动时，目标函数值随着不确定水平的升高呈现先高后低的特点，这是由于废旧产品的单位再制造成本虽然与废旧产品的回收量以及废弃量没有直接关系，但是废旧产品的回收量以及废弃量直接影响废旧产品的再制造量，从而影响目标总成本的走势，而废旧产品的单位再制造成本与废旧产品的回收量以及废弃量对目标总成本的影响方向相反，因此导致总成本走势线先高后低;当ρc=0，其他ρ同时变动时，目标函数值的走势几乎与“ρd变动，其他ρ=0”时一致.因此在本例所有不确定性因素中，产品的市场需求是十分重要的影响因素，废旧产品的单位再制造成本也会对系统产生较大但并不是十分关键的影响.因此，加大产品市场需求的预测力度，尽可能减少由于需求的不确定带来的总成本的增加，同时在对回收的废旧产品进行分拣和再制造时，要采用成熟稳定的技术，减少因为技术采用不当而造成的损失.

3)需求鲁棒性分析

由于市场需求对目标函数的敏感性最大，在市场需求变化时，需要验证目标函数的稳定性.令市场需求服从的均匀分布，在不同的 ρ值(ρ=0.2，0.5，0.8，1)下利用excel生成6组随机数，采用lingo9.0软件包进行求解，按照ρ的取值对每组数据的结果求均值，结果见到表9.

表9 市场需求的随机值和名义值下的目标函数值比较Table 9 Comparison of objective function values under nominal data and realizations of demands

如表9，当市场需求变动时，在不同的ρ值下，随机值下的目标函数值均比名义值下的目标函数值小，说明鲁棒优化模型取得了良好的结果.这是因为鲁棒优化考虑了这些不确定因素可能出现的最坏情况，并在这种最坏情况下最优化系统的总成本，因此，鲁棒优化具有良好的稳定性.

5 结束语

针对外部环境的不确定性，采用鲁棒优化方法对闭环供应链的网络构建进行了研究，建立了市场需求、回收产品的再制造成本、回收产品的回收量和回收中心的废弃量不确定条件下的多产品闭环供应链网络，并对各不确定性因素进行了敏感性分析.结果表明，市场需求最为敏感，其次为回收产品的再制造成本.最后通过相关数据比较，简要说明了鲁棒优化具有良好的稳定性.

References)

［1］Min H，Ko H J，Ko C S.A genetic algorithm approach to developing the multi-echelon reverse logistics network for product returns［J］.Omega，2006，34(1):56 -69.

［2］Lee J E，Gen M，Rhee K G.Network model and optimization of reverse logistics by hybrid genetic algorithm［J］.Computers＆ Industrial Engineering，2009，56(3):951-964.

［3］Pishvaee M S，Torabi S A.A possibilistic programming approach for closed-loop supply chain network design under uncertainty ［J］.Fuzzy Sets and Systems，2010，161(20):2668-2683.

［4］葛束，甘蜜.基于遗传算法的集成逆向物流的供应链网络设计［J］.中国铁道科学，2008，29(6):116 -120.Ge Shu，Gan Mi.Genetic algorithms based design of the supply chain netword integrated with the reverse logistics［J］.China Railway Science，2008，29(6):116 -120.(in Chinese)

［5］周永圣，汪寿阳.一种逆向物流网络设计模型［J］.交通运输系统工程与信息，2008，8(3):71-78.Zhou Yongsheng，Wang Shouyang.Generic model of reverse logistics network design［J］.Journal of Transportation Systems Engineering and Information Technology，2008，8(3):71 -78.(in Chinese)

［6］孙浩，达庆利.制造/再制造集成物流网络设施选址问题研究［J］.计算机集成制造系统，2009，15(2):362-368.Sun Hao，Da Qingli.Facility-location problem for an integrated manufacturing/remanufacturing logistics network［J］.Computer Integrated Manufactureing Systems，2009，15(2):362 -368.(in Chinese)

［7］刘琼，叶晶晶，邵新宇.不确定信息条件下制造/再制造物流网络优化设计［J］.华中科技大学学报:自然科学版，2007，35(10):80 -83.Liu Qiong，Ye Jingjing，Shao Xinyu.Design of logistics networks for manufacture/remanufacture in uncertain environment［J］.Journal of Huazhong University of Science and Technology:Nature Science Edition，2007，35(10):80-83.(in Chinese)

［8］谢家平，黄雪琪，陈荣秋.闭环供应链物流网络选址优化模型［J］.系统管理学报，2008，17(3):248 -255.Xie Jiaping，Huang Xueqi，Chen Rongqiu.Research on closed-loop supply chain network location model［J］.Journal of Systems ＆ Management，2008，17(3):248 -255.(in Chinese)

［9］谢家平，赵忠.基于GERT随机网络的废弃回收预测模型研究［J］.管理学报，2010，7(2):294-300.Xie Jiaping，Zhao Zhong.Forecasting model for the reusing process of the discarded products based on GERT network theory［J］.Chinese Journal of Management，2010，7(2):294 -300.(in Chinese)

［10］杨玉香，周根贵.随机需求下闭环供应链网络设施竞争选址模型研究［J］.控制与决策，2011，26(10):1553-1561.Yang Yuxiang，Zhou Gengui.Study on location model of facility competition for closed-loop supply chain network with random demands［J］.Control and Decision，2011，26(10):1553 -1561.(in Chinese)

［11］Ben-Tal A，Nemirovski A.Robust solutions to uncertain linear programs［J］.Operations Research Letters，1999，25(1):1-13.

［12］Pishvaee M S，Rabbani M，Torabi S A.A robust optimization approach to closed-loop supply chain network design under uncertainty［J］.Applied Mathematical Modeling，2011，35:637 -649.