基于神经网络的薄壁件加工变形预测方法

秦国华，张运建，叶海潮

(南昌航空大学 无损检测教育部重点实验室，江西 南昌330063)

0 引言

减小加工误差、提高零件的表面质量是制造企业追求的目标。在航空、航天、兵器等国防工业领域的高性能零件广泛采用复杂薄壁结构，其精度要求越来越高，如运用在雷达上的军品铝质薄壳件和薄筒件、飞机上的翼肋和发动机上的涡轮叶片等薄壁件，都具有尺寸大、刚度弱、表面精度高等特点，加工中采用数控铣削或数控车削成形。在这些结构件的加工中，由于其弱刚度、残余应力、过大切削力、切削热、不合理的刀具结构与切削参数等因素，引起工件产生加工变形，极端情况甚至报废。为了减小工件的变形，需对薄壁件切削加工进行深入研究。

有限元模拟能够揭示实验方法难以获得的切削力、应力、变形、材料失效应力等加工数据，目前许多学者利用有限元分析方法对薄壁件加工变形分析进行了大量研究。张臣等[1]视参与切削的切削单元受力之和为实际切削力，建立球头铣削过程中刀具的受力变形模型，研究了球头铣刀刀具变形引起的加工误差仿真分析方法。梅中义等[2]研究了残余应力对加工变形的影响，采用单元生死方法实现切削过程的仿真。然而，这些研究工作仅限于工况条件已知的工件变形有限元分析，不能实现工况未知条件下工件变形的预测。

在假定铣削速度、铣削深度、进给量和铣削宽度引起的工件变形量已知条件下，唐东红等[3]建立了铣削速度、铣削深度、进给量与工件变形之间的神经网络模型，通过均匀实验设计方法获得训练样本，最终利用Levenberg－Marquardt 算法实现对工件变形的预测。李目[4]在建立BP 神经网络非线性映射模型时，将铣削的主轴转速和每齿进给量作为BP 神经网络输入特征预测工件加工变形。而刘新玲等[5]根据切削刃对工件作用时间的先后对已加工表面上相应节点进行加载、卸载，利用载荷步方法对动态切削力引起的工件变形进行有限元分析，通过BP 神经网络算法建立了摆线轮铣削力与加工变形的预测模型。上述工件变形的预测方法仅考虑了铣削工艺参数的影响，而忽略了刀具的几何参数。

薄壁件切削加工过程中引起加工变形的影响因素多种多样，多个影响因素的组合则更是成千上万。显然，仅仅根据加工变形的影响因素利用有限元方法分析计算工件的加工变形，是不切实际的。为此，本文针对薄壁件铣削过程建立了加工变形的有限元仿真模型，分析了刀具几何参数对加工变形的影响规律，并利用实验数据验证了有限元分析模型的有效性。借助BP 神经网络的非线性映射能力，建立了铣刀前角、螺旋角与工件加工变形的非线性映射模型，从而实现了利用有限的变形分析结果预测任意前角、螺旋角引起的加工变形。该方法不仅为实际加工实现智能化提供条件，还为薄壁件切削参数优化和路径补偿提供有效数据。

1 薄壁件加工变形的有限元仿真技术

加工过程仿真技术是一项基于工程力学与有限元方法的虚拟制造技术。本文通过切削过程的合理建模、有限元分析计算及数值结果的静动态可视化后置处理，无须对工件进行试切即可获得切削温度、切削力和切削应力的分布形式以及工件和刀具的变形状况的相关数据。

1.1 有限元分析模型

如图1 所示为薄壁件的铣削加工示意图，薄壁部分尺寸分别为:长l =50 mm，高h =25 mm，壁厚t=4 mm，工件材料为铝合金7050－T7451.加工过程采用螺旋角β =30°、前角γ0=20°的双齿圆柱立铣刀，刀具直径d =10 mm，刀具材料为硬质合金YG8.加工参数为径向铣削宽度ap=2 mm，轴向铣削深度aw=25 mm，每齿进给量fz=0.125 mm，主轴转速n=1 200 r/min，摩擦系数μ=0.3.

图1 薄壁件铣削仿真示意图Fig.1 The simulation diagram of the thin－walled workpiece milling

1.2 工件材料的本构模型

1.2.1 材料的本构关系

Johnson－Cook 准则利用变量乘积关系分别描述应变、应变率和温度的影响，常用于模拟金属材料从低应变率到高应变率下的动态行为。Johnson－Cook准则具体表述为

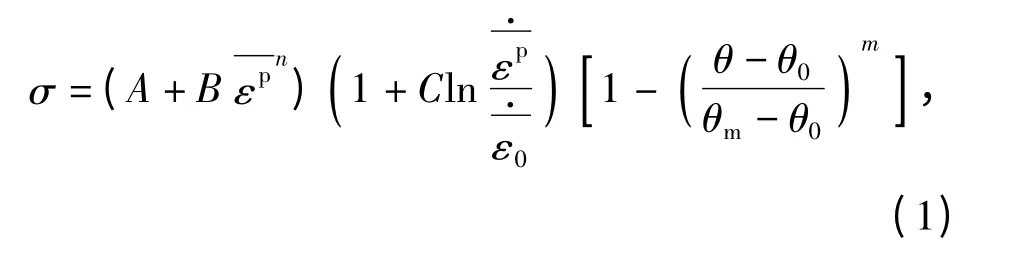
随着刀具的切入，当工件材料的等效塑性应变D 达到1.0 时，材料失效，实现被切单元与工件脱离。其失效准则是把每个工件单元定义为等效塑性应变，即

1.3 材料模型参数

铝合金7050－T7451 的密度为2 820 kg/mm3，弹性模量为71.7 GPa，泊松比为0.33.另外，7050－T7451 的热导率、线热膨胀系数以及比热容参数如表1 ～表3 所示[7]。

表1 热导率Tab.1 Thermal conductivity

表2 线膨胀系数Tab.2 Thermal expansion

由于Johnson－Cook 材料本构模型引入了应变率强化、应变硬化以及热软化参数，综合反映了金属材料大应变、高应变率和高温加载下的本构关系，对各种材料参数均适用且形式简单，所以本文选用该模型。7050－T7451 的Johnson－Cook 材料本构模型参数如表4 所示[7]。Johnson－Cook 材料失效准则参数如表5 所示。

表3 比热容Tab.3 Specific heat

表4 材料模型参数Tab.4 Constants of the Johnson－Cook constitutive model

表5 材料失效准则参数Tab.5 Fracture parameters

所用刀具为硬质合金YG8，其化学成分为92%的WC 和8% 的Co，密度为14.4 ～14.6 kg/m3，YG8 的耐磨性良好，使用强度和冲击韧性非常优秀。适用于铸铁、有色金属及其合金、非金属材料的粗加工，在铝合金材料的铣削过程中变形量很小。YG8 的主要物理与热力学性能如表6 所示[8]。

表6 刀具的物理与热力学性能Tab.6 Material parameters of the cutting tool

1.4 仿真结果分析

根据有限元仿真计算结果，获得工件的变形云图，如图2 所示。

实验是在Micron UCP710 五轴加工中心上进行的，铣削方式为单向走刀、顺铣，铣削参数与仿真过程相同[4]。由于工件在x 方向上变形最大，故于铣削完成后，在已加工表面上取y =10 mm，25 mm，40 mm 3 条垂直线，分别沿z 轴方向任意取z=0.5 mm，2.5 mm，5 mm，7.5 mm，10 mm，12.5 mm，15 mm，18 mm，22 mm 共9 个点。利用Global Classic 9128型三坐标测量机分别对9 个点加工前与加工后的x轴坐标值进行测量，其差值即为加工变形的大小，其变形曲线如图3 所示。另外，在加工表面z =8 mm处，沿y 方向分别取y = 1 mm，5 mm，10 mm，15 mm，20 mm，25 mm，30 mm，35 mm，40 mm，45 mm，49 mm 共11 处工件变形数据，绘制出工件的加工变形状态，如图4 所示。进行对比分析后可知，无论是仿真结果的大小，还是变形趋势，都与实验值具有较好的吻合度，从而验证了图1 中薄壁件有限元分析模型的正确性。

图2 薄壁件的变形云图Fig.2 Deformation nephogram of the thin－walled workpiece

2 薄壁件加工变形的神经网络预测方法

由第1 节内容可知，利用有限元方法可以分析给定刀具前角与螺旋角情况下薄壁件的变形状态。然而，刀具前角、螺旋角的组合情况多种多样，不可能利用有限元方法一一计算与分析，否则费时费力也找不出刀具结构与加工变形之间的复杂关系。因此，本节将建立基于BP 神经网络的薄壁件加工变形预测方法，实现对刀具角度的有效性评估与修改，最终保证零件的加工质量，缩短制造周期，降低制造成本。

2.1 BP 网络结构的确定

BP 神经网络是一种具有3 层或3 层以上的前馈神经网络，包括输入层、隐藏层和输出层，可任意的精度逼近任意的连续函数[9]。Hecht－Nielsen 证明具有1 个隐藏层的3 层前馈型网络可以逼近任何多变量函数，故本文采用1 个3 层BP 神经网络进行铣削变形的预测。BP 网络结构如图5 所示，输入层有刀具前角和螺旋角2 个神经元，输出层有1 个神经元，即需预测的由刀具结构产生的最大变形量，再根据Kolmogorov 定理，并综合考虑网络的学习速度和泛化能力，最终确定隐含层包含4 个神经元。

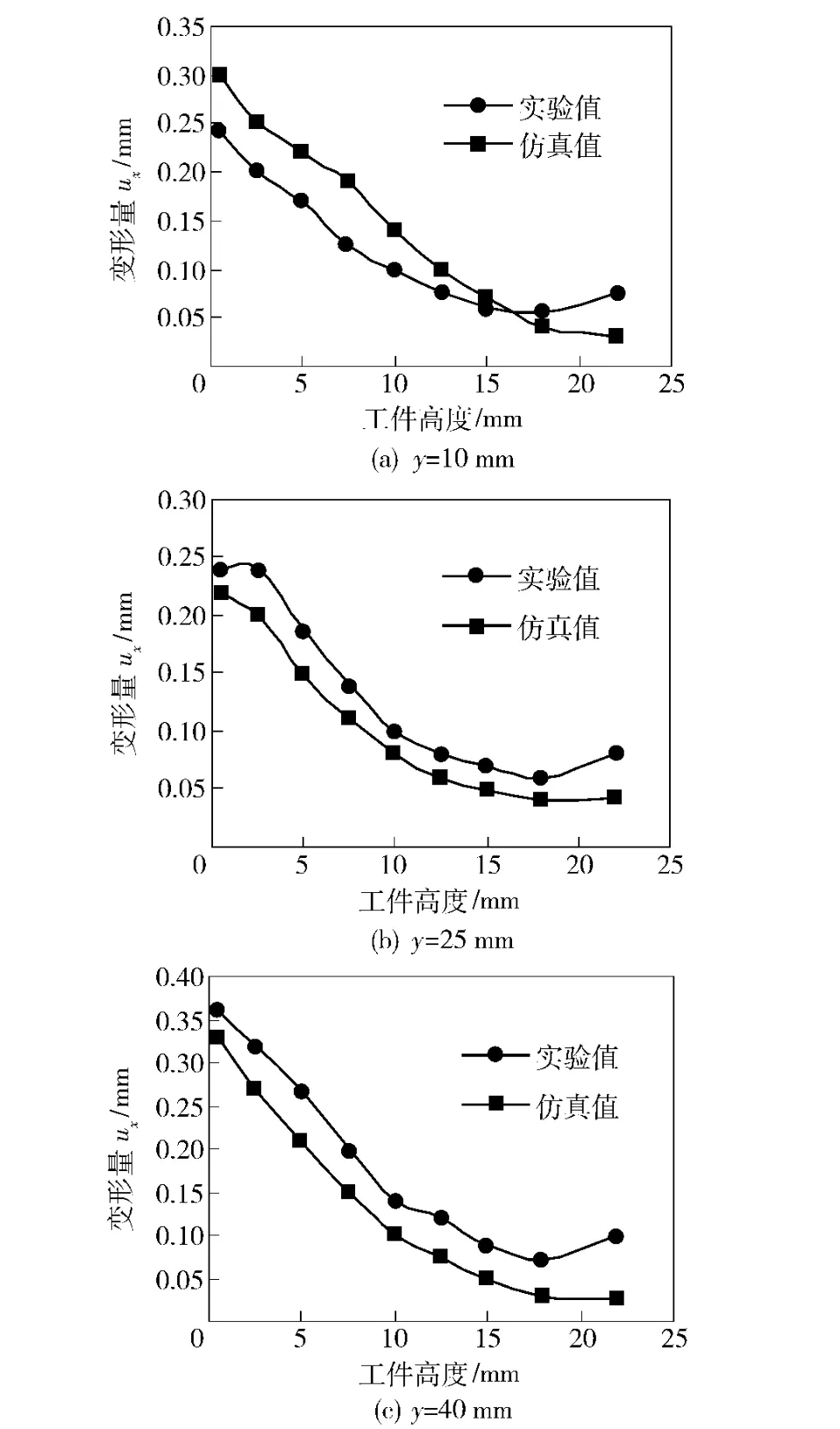
图3 垂直线的加工变形模拟值与实验结果的比较Fig.3 Comparison of the simulated values of the vertical line deformations with the experimental results

图4 水平线的加工变形模拟值与实验结果的比较Fig.4 Comparison of the simulated values of the horizontal line deformations with the experimental results

2.2 训练样本的选择

图5 BP 网络结构图Fig.5 Configuration of BP neural network

根据训练样本的相容性、遍历性和致密性3 要素要求，螺旋角的采样间隔15°，分别取30°，45°，60°，而前角的采样间隔5°，分别取－10°，－5°，0°，5°，10°，15°，20°，25°，30°，最后以14 种工况下铣刀引起的工件最大变形作为网络的训练样本。利用第1 节已经验证过的有限元分析方法，容易获得工件的最大变形，如表7 所示。

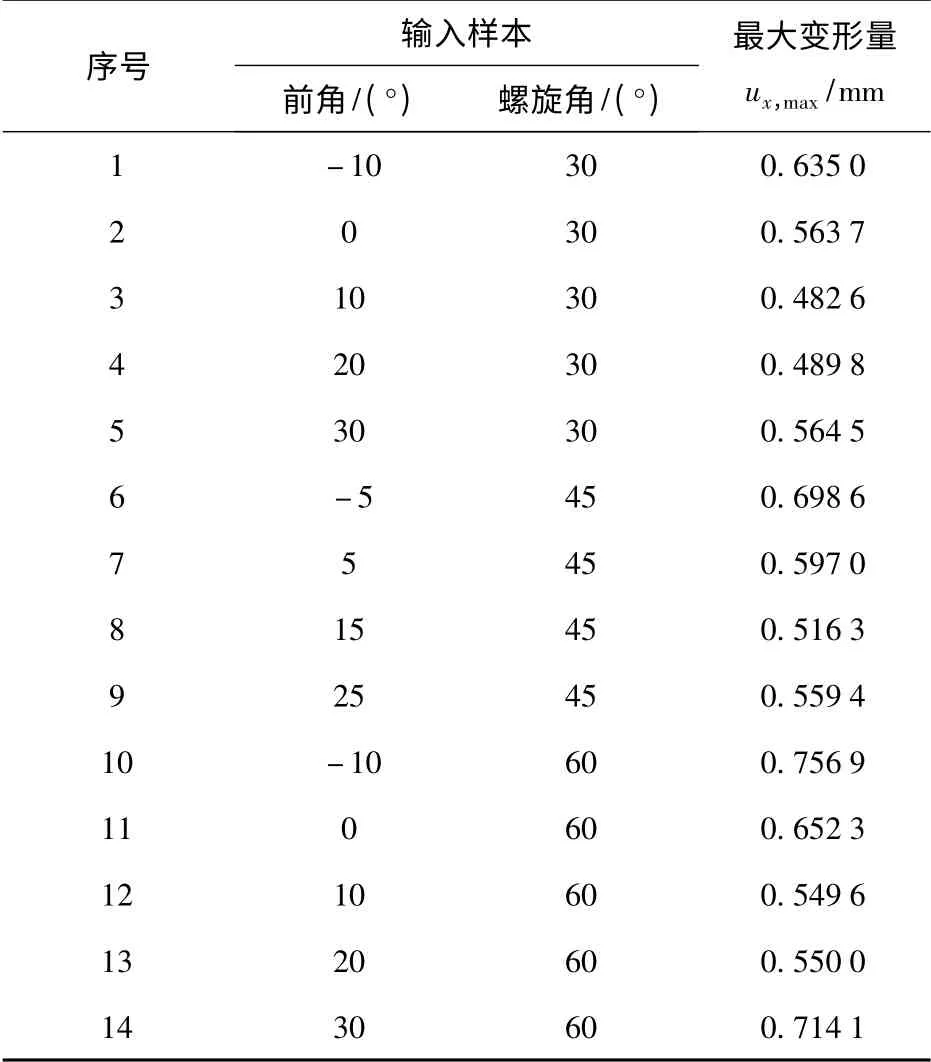
表7 不同铣刀角度下的切削变形Tab.7 Workpiece deformations under different angle of milling cutter

2.3 神经网络的训练

由于基于高斯－牛顿法改进得到的Levenberg－Marquardt 算法在实际应用中具有很快的收敛速度，故选择Levenberg－Marquardt 算法作为前馈型神经网络的学习算法对权系数进行更新和计算，实现输入与输出间的非线性映射。由于系统是非线性的，初始权值对于学习能否达到局部最小和是否能够收敛的影响很大，这就要求初始权值在输入累加时使每个神经元的状态值接近于0，输入样本要进行归一化处理，使那些比较大的样本数据输入仍落在传递函数梯度大的地方，可以采用(4)式进行归一化处理，使各个样本数据都落在[0，1].

式中:xi(i =1，2，…，14)为第i 个输入样本;xmin与xmax分别为样本最小值和最大值。

样本归一化后，就可进行网络训练。根据BP神经网络的一般设计原则及大量实验，训练中隐藏层神经元的传递函数为双曲正切函数，实现不同样本的空间分割，而输出层神经元的传递函数为线性函数，输出网络的识别结果。初始化网络权系数在[0，1]之间，学习误差为0.000 001.将表7 中的14 个样本输入网络进行训练，网络在63 步收敛到要求精度，神经网络训练过程误差曲线如图6 所示。

图6 网络训练结果Fig.6 Results of network training

利用仿真函数sim 对上述网络进行预测，并将预测值与仿真值对比，如表8 所示。由此可见，测试样本的网络输出值与有限元计算结果之间的误差不超过3%.

3 结论

1)本文以薄壁件铣削过程有限元仿真模型为基础，利用BP 神经网络卓越的学习能力，有效地建立了铣刀角度与加工变形之间的非线性逻辑关系。通过表8 数据可以看出，该网络结构预测结果误差合理。

2)BP 神经网络具有较高的精度和良好的泛化能力，只要选择合适的网络结构、传递函数和训练参数，合理地设计训练样本，神经网络模型就可以有效地用来预测薄壁件的变形量。这些利用BP 神经网络预测的数据还可以作为样本数据，采用遗传算法对铣刀的前角与螺旋角进行优化，有效地实现薄壁件铣削变形的控制。

表8 样本测试数据输出值与有限元计算结果比较Tab.8 Comparison of the predicted results with the simulated values

References)

[1]张臣，周来水，安鲁陵，等.刀具变形引起的球头铣刀加工误差建模[J].南京航空航天大学学报，2008，40(1):94 －99.ZHANG Chen，ZHOU Lai－shui，AN Lu－ling，et al.Modeling of ball－end milling cutter deflection－induced machining error[J].Journal of Nanjing University of Aeronautics and Astronautics，2008，40(1):94 －99.(in Chinese)

[2]梅中义，高红，王运巧.飞机铝合金结构件数控加工变形分析与控制[J].北京航空航天大学学报，2009，35(2):146 －150.MEI Zhong－yi，GAO Hong，WANG Yun－qiao.Analyzing and controlling distortion of aircraft aluminium alloy structural part in NC machining[J].Journal of Beijing University of Aeronautics and Astronautics，2009，35(2):146 －150.(in Chinese)

[3]唐东红，孙厚芳，王洪艳.用BP 神经网络预测数控铣削变形[J].制造技术与机床，2007，(8):48 －50.TANG Dong－hong，SUN Hou－fang，WANG Hong－yan.Milling deformation forecast with BP neural network[J].Manufacturing Technology ＆ Machine Tool，2007，(8):48 －50.(in Chinese)

[4]李目.基于变形控制的薄壁件铣削加工参数优化及仿真研究[D].南京:南京航空航天大学，2008.LI Mu.Research on the optimization of milling parameters and simulation of thin－walled parts based on the machining errors control[D].Nanjing:Nanjing University of Aeronautics and Astronautics，2008.(in Chinese)

[5]刘新玲，戚厚军.基于神经网络的铣削复杂薄壁件受力变形分析和建模研究[J].机械制造，2009，47(535):3 －5.LIU Xin－ling，QI Hou－jun.Forced deformation analysis and modeling research of milling of complex thin－walled parts based on neural network[J]，Machinery，2009，47(535):3 － 5.(in Chinese)

[6]Johnson R，Cook W K.A constitutive model and data for metals subjected to large strains high strain rates and high temperatures[C]∥Proceedings of the 7th International Symposium on Balistics.Hague:IBC，1983:541 －547.

[7]张士林，任颂赞.简明铝合金手册[M].上海:上海科学技术出版社，2001.ZHANG Shi－lin，REN Song－zan.Brief handbook of aluminium alloy[M].Shanghai:Shanghai Science and Technology Press，2001.(in Chinese)

[8]陈献廷.硬质合金使用手册[M].北京:冶金工业出版社，1986.CHEN Xian－ting.Handbook of hard alloys[M].Beijing:Metallurgical Industry Press，1986.(in Chinese)

[9]薛嘉庆.最优化原理及方法[M].北京:冶金工业出版社，1992.XUE Jia－qing.Optimization principles and methods[M].Beijing:Metallurgical Industry Press，1992.(in Chinese)