RBF神经网络模型在砂土液化判别中的应用研究
勾丽杰,刘家顺
(1.辽宁省交通高等专科学校信息系,沈阳 110122;2.辽宁工程技术大学土木与交通学院,辽宁阜新 123000)
RBF神经网络模型在砂土液化判别中的应用研究
勾丽杰1,刘家顺2
(1.辽宁省交通高等专科学校信息系,沈阳 110122;2.辽宁工程技术大学土木与交通学院,辽宁阜新 123000)
以时松孝次收集的砂土液化数据为研究对象,选取黏粒含量ρc、相对密实度Dr、临界深度ds、竖向有效应力σ'、地下水位dw、地震震级M、最大地面水平加速度αmax和标准贯入次数SPT-N等8个砂土液化的主要影响因素作为RBF神经网络的输入参数,利用MATLAB7.0中的神经网络工具箱,对部分样本数据进行训练和测试。并利用建立的RBF神经网络模型分析了各因素对砂土液化的影响规律。结果表明:砂土液化判别指标随αmax的增加而增大,随SPT-N和dw的增加而减小。研究成果表明,建立的RBF网络模型完全满足砂土液化判别的精度要求,能够精确模拟输入和输出之间复杂的非线性映射关系,具有较高的预测精度,具有重要的工程应用价值。
砂土液化;评价指标;RBF神经网络;液化等级
1 研究背景
自1964年美国Alaska地震、日本新泻地震以及2008年中国汶川地震造成大量地面沉陷、建筑物破坏以来,地震引起的地基土液化、地基失效、边坡失稳等问题引起了国内外学者和工程界的高度重视。目前对地基土液化产生的原因、影响因素和液化作用机理等方面的研究取得了大量具有应用价值的研究成果[1-2],特别是对地基土液化判别的研究已经具有多种分析方法。归纳起来主要有试验分析法和经验法2类[3]。室内试验存在仪器精度不足、试验条件简化和对土体地震反应分析结果的可信度有争议等问题,导致了室内试验分析方法还无法在土体液化判别中广泛应用。经验判别方法以地震场地液化调查资料为基础,利用数理统计法[4]、模糊综合评判法[5]、灰色聚类法[6],给出判别液化的条件和标准,具有广泛应用性。由于砂土液化的影响因素包括诸如地震震级、地震烈度、持续时间、土体颗粒组成、含水量、静偏应力和地下水位等,且各影响因素与砂土液化与否并非简单的线性关系,导致砂土液化的判定十分困难,其判别结果也并不准确[7]。
人工神经网络ANN(Artificial Neural Network)克服了模式、语音识别和非结构信息处理方面的缺陷,在模式识别、智能控制、组合优化和预测等领域取得了重要进展,在解决非线性问题上具有独特的优越性。ANN可以通过大量样本的学习来抽取隐含在样本中的因果关系,从数据中提取事物特征,在信息不准确、背景知识不清楚或推理规则不明确的情况下依然能进行推理判断。
为准确描述砂土液化与各影响因素之间复杂的映射关系、提高砂土液化势评价的可靠性和准确性,本文将ANN技术引入到砂土液化评判问题中,采用函数逼近能力、数据拟合能力和收敛速度都明显优于BP网络的RBF网络,用于砂土液化势评价,建立各主要影响因素与地基土液化之间的非线性关系。即实现神经网络模型对砂土液化势的自动预估,并利用该模型建立了各因素影响趋势线,通过对该神经网络模型的建立、运行和检验,得到了各因素对砂土液化的影响规律。
2 RBF神经网络模型的原理
目前,常用的前馈型神径网络模型包括误差反向传播BP网络模型和RBF网络模型2种[8]。二者不同之处在于BP模型用于函数逼近时,采用负梯度下降法调节权值,存在着收敛速度慢和结果局部极小等缺陷。而RBF网络的作用函数则是局部的,在逼近能力、分类能力和学习速度等方面均优于BP网络模型,训练样本越多,向量维数越高,其优势越明显[9]。
2.1 RBF神经网络模型
RBF神经网络模型是一种将输入矢量扩展或者预处理到高维空间中的神经网络模型,该模型由输入层、隐层和输出层3层构成,其模型结构如图1所示。

图1 RBF神经网络模型结构图Fig.1Structure of the RBF neural network model
2.2 RBF神经网络的核函数
输入层节点只是将输入样本信号传递到隐层,RBF节点通常是由径向对称的辐射状核函数构成,核函数的形式主要有以下几种,如式(1)至式(3)所示:

RBF节点中的核函数对输入信号在局部产生响应,即当输入样本信号接近样本向量的中心范围值时,RBF节点将产生较大的输出,这种网络具有局部逼近能力。RBF节点作用核函数较为常用的是Gauss核函数,如式(4)所示:

式中:μj为第j个隐层节点的输出;X=(x1,x2,…,xn)T为输入样本信号;Cj为Gauss核函数的中心值;σj为标准化常数;Nh为隐层节点数。
由式(4)可知,节点的输出范围在0~1之间,且输入信号越靠近节点的中心,输出的值越大。由式(4)还可以看出Gauss核函数具有形式简单、径向对称、光滑性好、解析性好、便于理论分析等优点。
为提高神经网路精度和减少隐层节点数,可将网络基函数改成多变量正态密度函数,见式(5)。
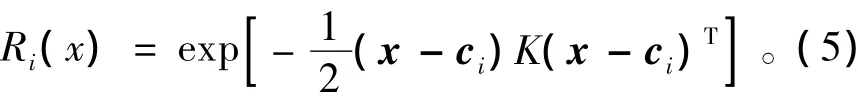
式中:K=E[(x-ci)T(x-ci)-1]是输入协方差阵的逆;x为n维输入向量;ci为第i个基函数的中心,与x具有相同维数的向量。
2.3 RBF学习过程
RBF神经网络的输出为隐层节点(也称RBF节点)输出的线性组合,见式(6)所示。

RBF神经网络学习过程第1阶段为预处理阶段。采用无教师识别方法,根据输入样本的位置分布情况,决定隐层各节点的Cj和σj,也可从样本向量中随机选取其值;第2阶段为学习权值阶段。预设好隐层参数后,根据最小二乘原则,求出输出层的权值Wi。可根据样本信号,对隐层和输出层的参数进行调节,以提高网络的精度。
3 基于RBF神经网络模型的砂土液化预测方法
3.1 RBF神经网络模型的建立
考虑到液化判别指标应具代表性以及现场测试的简便性,本文选取黏粒含量ρc、相对密实度Dr、临界深度ds、竖向有效应力σ'、地下水位dw、地震震级M、最大地面水平加速度αmax和标准贯入(简称标贯)次数SPT-N等8个砂土液化的主要影响因素作为RBF神经网络的输入参数。设输入层神经元数为8,输出层神经元数为2。利用MATLAB 7.0中的NEWRB函数自动确定所需隐层单元数并训练网络[10-11]。
3.2 RBF网络训练目标
依据时松孝次等人的研究成果和参考行业规范[12],将砂土液化势的分类标准定为4级,如表1所示。

表1 砂土液化分级标准Table 1Description of sand liquefaction levels
对应训练样本,设定相应目标值,如表2所示。将4类样本的期望输出参数依次设定为:<0.25 (未液化),0.25~0.5(临界液化),0.5~0.75(中等液化),0.75~1(严重液化)。
3.3 RBF神经网络模型评价
根据以上所建立的RBF神经网络模型,共选取40组时松孝次收集的砂土液化势数据[12],随机选取25组数据作为训练样本进行训练,选取15组数据作为测试样本,对所建立的RBF网络的正确性和智能性加以检验。RBF网络训练结果、测试结果及判定标准见表2和表3。
依据上述建立的RBF神经网络模型,对表2中数据进行训练时,迭代213次时,网络精度即达到5×10-4,且训练结果与实际结果全部吻合,完全满足砂土液化势判别的精度要求。这说明所建立的RBF神经网络模型具有较好的模拟效果,能够精确模拟输入和输出之间复杂的非线性映射关系。在对另15组数据运用上述建立的RBF网络模型,进行测试时,样本点与实测结果亦完全相同。这说明RBF网络模型具有较强的容错性和自适应性,同时也有较高的预测精度。

表2 时松孝次收集的砂土液化势数据及RBF网络训练结果Table 2Data of sand liquefaction potential collected by Tokimatsu Kohji and training results of RBF network
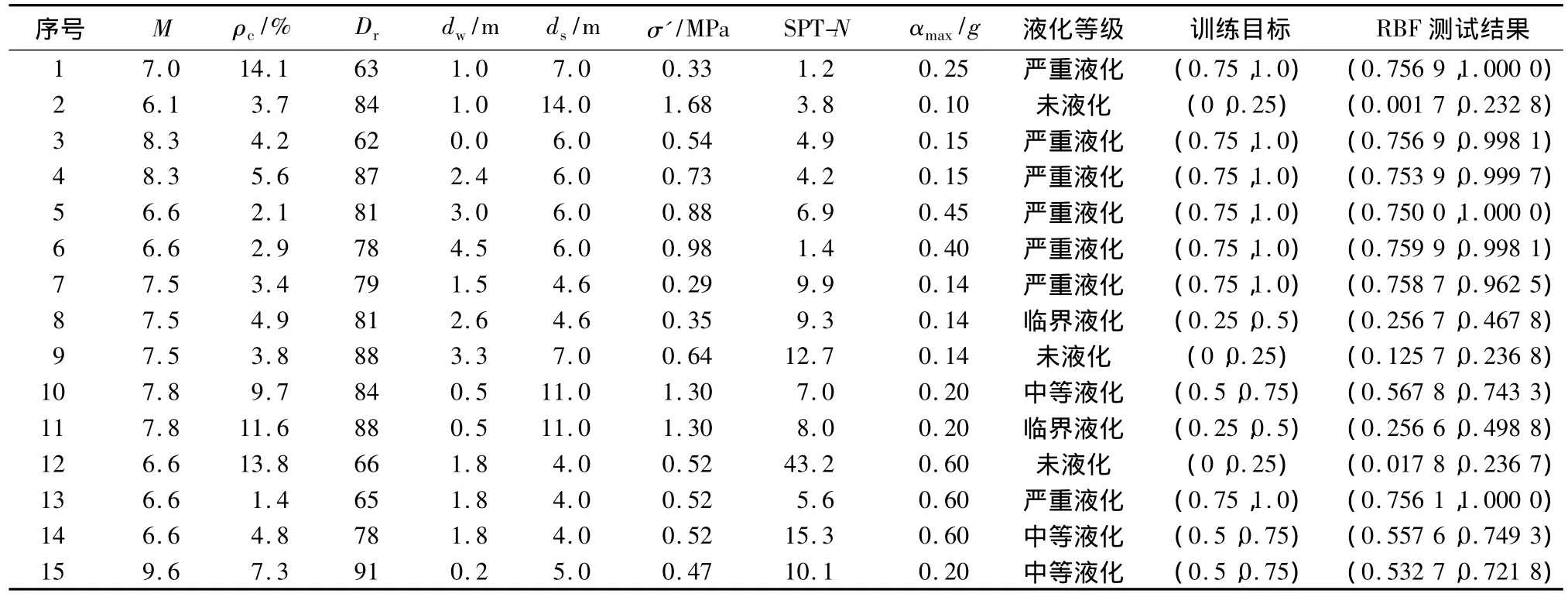
表3 时松孝次收集的砂土液化势数据及RBF网络测试结果Table 3Data of sand liquefaction potential collected by Tokimatsu Kohji and testing results of RBF network
4 砂土液化的主要影响因素分析
4.1 各因素的相对贡献率分析
各因素对砂土液化的影响程度是不同的。为研究各影响因素对砂土液化判别指标的相对贡献,利用MATLAB 7.0神经网络工具箱中的权重,计算出各因素对液化判别指标的相对贡献率[13]。
相对贡献率的计算公式为
C8=W8/W×100%。(7)
式中:W8为各因素隐层节点与输入节点间的网络权重;W为各因素权重之和。计算结果见表4。

表4 各因素的相对贡献率Table 4Results of relative contribution of each factor
从表4中可见,各因素对砂土液化的相对贡献率在10.36%~15.62%之间,说明所选取的因素对砂土液化影响显著,从而证明了RBF网络模型中各因素选择的正确性。进一步分析表4可知,αmax对砂土液化的贡献率最大,SPT-N和dw对砂土液化的贡献次之。αmax对砂土液化贡献率大的主要原因是其越大,对土体所产生的循环剪应力越大,也就使得砂土发生液化的可能性增加。SPT-N与ρc,Dr,ds和σ'等因素相互关联,而从表4中可以看出,这些因素与砂土液化关系密切。所以工程中很早就采用标贯击数法来判断砂土发生液化的可能性。地下水位以下的土颗粒处于悬浮状态,所以饱水砂土以上的覆盖层压力减小,从而使砂土发生液化。
4.2 各因素对砂土液化的影响规律分析
由表2和表3可知,采用RBF神经网络建立砂土液化预测模型是有效的,经过对学习样本的训练后,RBF神经网络模型已建立了各输入参数(影响因素)与输出参数(液化判别指标)之间的非线性映射关系。为进一步研究各因素对砂土液化的影响规律,建立各参数与砂土液化判别指标之间的关系曲线。即令某一影响因素变化,其余因素取为定值,形成若干组输入向量,并将其输入已训练完的RBF神经网络模型,得到该影响因素与砂土液化判别指标之间的关系曲线,称之为因素影响趋势线[13]。
由上文分析可知,SPT-N与ρc,Dr,ds和σ'等因素相互关联,为简化分析计算,本文利用所建立的RBF神经网络模型探讨了αmax,SPT-N和dw对砂土液化判别指标的影响规律。用训练好的网络模型得到砂土液化判别指标和上述3因素之间的关系,见图2至图4所示。

图2 最大地面水平加速度αmax与砂土液化判别指标的关系Fig.2Relation between maximum horizontal ground acceleration αmaxand evaluation index of sand liquefaction

图3 标贯击数SPT-N与砂土液化判别指标的关系Fig.3Relation between standard penetration number SPT-N and evaluation index of sand liquefaction

图4 地下水位dw与砂土液化判别指标的关系Fig.4Relation between groundwater level dwand evaluation index of sand liquefaction
从图2中可以看出,砂土液化判别指标随αmax的增加而增大,进一步分析图像可发现,最大地面水平加速度(αmax)与砂土液化判别指标近似呈对数函数关系增长,拟合参数见表5。
图3为标贯击数SPT-N与砂土液化判别指标的关系曲线。标贯击数SPT-N越大说明土体越密实,也就越难液化,砂土液化判别指标就越小。通过数据拟合可知,二者近似呈3次多项式函数关系,拟合参数见表5。
从图4可以看出,砂土液化判别指标随地下水位dw的增加而减小,且二者呈简单的线性关系,拟合参数见表5。

表5 液化判别指标与αmax,SPT-N和dw的拟合系数Table 5Fitting coefficients between evaluation index and αmax,SPT-N,dwrespectively
上述结果符合最大地面水平加速度αmax,SPT-N和dw等因素对砂土液化判别指标影响的研究结果,能够反映各上述3因素对砂土液化的影响规律。
5 结论
以时松孝次砂土液化势数据为研究对象,建立砂土液化预测的RBF神经网络模型,分析各因素对砂土液化的影响,主要结论如下:
(1)根据时松孝次收集的砂土液化势数据,随机选取25组数据作为训练样本进行训练,选取15组数据作为测试样本,对所建立的RBF网络的正确性和智能性加以检验。样本训练结果表明:所建立的RBF网络模型训练结果与实际结果全部吻合,完全满足砂土液化势判别的精度要求,能够精确模拟输入和输出之间复杂的非线性映射关系。样本测试结果表明:RBF网络模型具有较强的容错性和自适应性,同时也有较高的预测精度。
(2)利用MATLAB7.0工具,研究了各影响因素对砂土液化判别指标的相对贡献,计算出各因素对液化判别指标的相对贡献率。计算结果表明:各影响因素对砂土液化的相对贡献率在10.36%~15.62%之间,αmax对砂土液化的贡献率最大,标贯击数SPT-N和地下水位dw对砂土液化的贡献次之。
(3)利用所建立的RBF网络模型探讨了地震水平最大加速度αmax、标贯击数SPT-N和地下水位dw对砂土液化判别指标的影响规律。结果表明:砂土液化判别指标与αmax呈对数关系增加,与标贯击数SPT-N呈3次多项式函数关系降低,随地下水位dw的增加呈简单的负线性关系。
[1]RAHMAN M S,WANG Jun.Fuzzy Neural Network Models for Liquefaction Prediction[J].Soil Dynamics and Earthquake Engineering,2002,22(8):685-694.
[2]BAZIAR M H,JAFARIAN Y.Assessment of Liquefaction Triggering Using Strain Energy Concept and ANN Model Capacity Energy[J].Soil Dynamics and Earthquake Engineering,2007,27(12):1056-1072.
[3]李方明.人工神经网络在砂土液化判别及震陷预估中的应用[D].南京:南京工业大学,2005.(LI Fang-ming. Application of Artificial Neural Network in the Estimation of Sand Liquefaction and the Prediction of Earthquake-Induced Ground Settlement[D].Nanjing:Nanjing University of Technology,2005.(in Chinese))
[4]CETIN K O,SEED R B,KIUREGHIAN A D,et al. Standard Penetration Test-Based Probabilistic and Deterministic Assessment of Seismic Soil Liquefaction Potential[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2004,(12):1313-1340.
[5]季倩倩.砂土地震液化的优化判别[J].岩土工程技术,2001,(3):155-159.(JI Qian-qian.Fuzzy Evaluation for Seismic Liquefaction Discrimination of Sands[J]Geotechnical Engineering Technique,2001,(3):155-159.(in Chinese))
[6]赵艳林,杨绿峰,吴敏哲.砂土液化的灰色综合评判[J].自然灾害学报,2000,9(1):72-79.(ZHAO Yan-lin,YANG Lv-feng,WU Min-zhe.Grey Synthetical Evaluation of Liquefaction of Sands[J].Journal of Natural Disasters,2000,9(1):72-79.(in Chinese))
[7]HANNA A M,DERIN U,SAYGILI G.Neural Network Model for Liquefaction Potential in Soil Deposits Using Turkey and Taiwan Earthquake Data[J].Soil Dynamics and Earthquake Engineering,2007,27(6):521-540.
[8]张德丰.MATLAB/Simulink建模与仿真实例精讲[M].北京:机械工业出版社,2010.(ZHANG De-feng.MATLAB/Simulink Modeling and Simulation Examples[M]. Beijing:China Machine Press,2010.(in Chinese))
[9]周瑞林,刘燕,赵胜利.基于RBF神经网络的砂土液化预测[J].河南大学学报(自然科学版),2005,35 (4):101-105.(ZHOU Rui-lin,LIU Yan,ZHAO Shengli.Application of RBF Neural Network to Prediction of Sands Liquefaction Potential[J].Journal of Henan University(Natural Science),2005,35(4):101-105.(in Chinese))
[10]陈国兴,李方明.基于径向基函数神经网络模型的砂土液化概率判别方法[J].岩土工程学报,2006,28(3): 301-306.(CHEN Guo-xing,LI Fang-ming.Probabilistic Estimation of Sand Liquefaction Based on Neural Network Model of Radial Basis Function[J].Chinese Journal of Geotechnical Engineering,2006,28(3):301-306.(in Chinese))
[11]李菊凤,宁立波,周建伟,等.基于RBF神经网络的软基沉降预测研究[J].湖南科技大学学报(自然科学版),2005,20(3):49-53.(LI Ju-feng,NING Li-bo,ZHOU Jian-wei,et al.Research of Settlement Prediction of Soft Foundation Based on RBF Neural Networks[J]. Journal of Hunan University of Science&Technology (Natural Science Edition),2005,20(3):49-53.(in Chinese))
[12]TOKIMATSU KOHJI.Empirical Correlation of Soil Liquefaction Based on SPT N-Value and Fines Content[J].Soils and Foundation,1983,23(4):56-74.
[13]陈国兴,李方明.基于RBF神经网络模型的砂土液化震陷预估法[J].自然灾害学报,2008,17(1):180-186. (CHEN Guo-xing,LI Fang-ming.Seismic Settlement Estimation of Sand Liquefaction Based on RBF Neural Network Model[J].Journal of Natural Disasters,2008,17(1): 180-186.(in Chinese))
(编辑:姜小兰)
Application of RBF Neural Network Model to Evaluating Sand Liquefaction
GOU Li-jie1,LIU Jia-shun2
(1.Department of Information,Liaoning Provincial College of Communications,Shenyang110122,China; 2.School of Civil Engineering and Transportation,Liaoning Technical University,Fuxin123000,China)
The neural network toolbox of MATLAB7.0 was used to train and test some sample data of sand liquefaction collected by Tokimatsu Kohji.Eight eigenvectors:clay content(ρc),relative compaction(Dr),critical depth of soil layer(ds),vertical effective stress(σ'),groundwater level(dw),magnitude of earthquake(M),maximum horizontal ground acceleration(αmax)and standard penetration number(SPT-N)were selected as input parameters of the RBF neural network.Furthermore,the established RBF neural network model was used to analyze the effect of each factor on the sand liquefaction.Results of the relative contribution of each factor showed that αmaxwas the biggest influencing factor on the evaluation index of sand liquefaction,followed by SPT-N and dw.The evaluation index increased with the rise of αmax,while reduced with the increase of SPT-N and dw.The evaluation index shows a logarithmic relation with αmax,cubic polynomial relation with SPT-N,and a negative linear relation with dw.It’s revealed that the established RBF network model fully meets the requirement of evaluation accuracy for sand liquefaction.It can simulate the complex nonlinear mapping relation between the input and output data and also gives high prediction precision.
sand liquefaction;evaluation index;RBF neural network;liquefaction level
TU478
A
1001-5485(2013)05-0076-06
10.3969/j.issn.1001-5485.2013.05.017
2013,30(05):76-81
2012-09-19;
2012-12-15
勾丽杰(1983-),女,辽宁黑山人,副教授,主要从事应用数学的教学与研究工作,(电话)15802451668(电子信箱)glj_5188@yahoo. com.cn。
刘家顺(1986-),男,辽宁铁岭人,博士,主要从事土力学与地基基础的研究工作,(电话)13941892585(电子信箱)liujiashun@163. com。

