用于机械压力机伺服直驱的开关磁通永磁电机的设计与优化
梁锦涛,赵升吨,谢 嘉,赵永强,3
(1.西安交通大学机械工程学院,陕西西安710049;2.上海海洋大学工程学院,上海201306;3.陕西理工学院机械工程学院,陕西汉中723000)
0 引言
机械压力机是金属成形加工领域广泛使用的锻压设备[1],目前已发展到由交流伺服电机伺服直驱的第三代机械压力机。实现机械压力机的伺服直驱能够提高压力机工作效率,降低能耗和噪声,提高滑块运动可控性[2]。但由于交流伺服电机扭矩和功率密度较低,使得电机造价昂贵;同时传动系统还需要保留大惯量飞轮[3],不利于实现压力机的柔性化加工。交流伺服压力机的研制很大程度上取决于直驱电动机的性能参数。开关磁阻电动机(Switched Reluctance Motor,SRM)作为一种结构简单、成本低、鲁棒性好和运行可靠性高的调速电机,在压力机驱动领域得到广泛研究和应用[4-6]。但由于SRM的输出力矩完全由磁阻转矩构成,其扭矩密度甚至比现行交流伺服电机还低,同时还存在较大的力矩脉动,并不是压力机伺服直驱的理想动力源。
随着现代电机设计与应用技术的发展,出现不同拓扑形式的永磁电机。开关磁通永磁电机(Flux Switching Permanent Magnet Motor,FSPMM)是一种永磁体安装在定子上的电机[7],转子上只存在导磁铁心,结构上具有与SRM一致的鲁棒性,有利于承受压力机加工过程中的冲击载荷。FSPMM的永磁体和电枢绕组均放置在定子上,其磁场相互作用产生足够大的永磁力矩,具有较高的扭矩和功率密度。本文介绍FSPMM的拓扑结构及运行原理,并根据压力机的驱动要求首先对FSPMM的主要尺寸及参数进行理论计算,然后利用有限元法分析FSPMM的输出性能,并结合曲面响应法对FSPMM进行优化设计,从而提出一种用于伺服直驱机械压力机的FSPMM的设计与优化方法。
1 FSPMM的拓扑结构和运行原理
如图1所示为一种最为常见的三相12/10极的FSPMM拓扑结构,FSPMM的定子铁心制造成U形模块,周向充磁的永磁体间隔放置在两个U形铁芯模块之间,且相邻两个永磁体充磁方向相反,各相线圈以集中绕组的形式缠绕在两个U形铁芯齿和永磁体形成的“三文治”上。转子铁芯呈凸极式结构,当转子磁极与“三文治”结构中的一个齿对齐时,绕组的匝链磁通达到最大;如图2所示,当转子凸极与相邻定子齿对齐时,绕组匝链磁通方向反转且达到最大。在两者之间绕组匝链磁通和永磁体呈正弦波变化,因此FSPM的控制方法与传统永磁同步电机相同,通过磁场定向的矢量变换即可实现调速或伺服控制[8]。
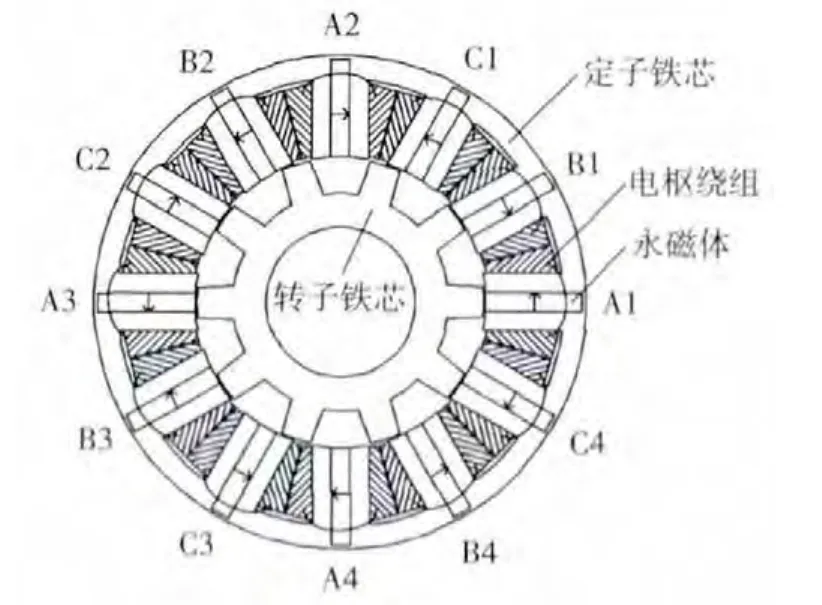
图1 12/10极FSPMM结构示意图
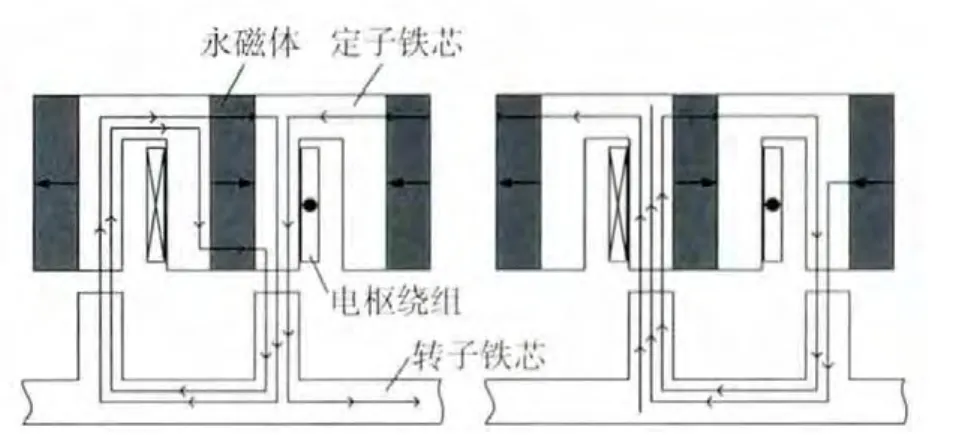
图2 FSPMM开关磁链变换示意图
FSPMM在结构上属于双凸极电机,电机转子极数、定子极数及绕组相数可根据不同的应用场合进行设计。另外,定子绕组及铁芯的拓扑结构也可以根据输出性能要求设计成不同形式[9]。
2 FSPMM主要尺寸及电磁参数估算
设计用于机械压力机伺服直驱的FSPMM需要根据压力机的驱动要求设计电机拓扑结构,并计算FSPMM的主要尺寸及电磁参数。以63t曲柄肘杆压力机[10]为例确定FSPMM的性能参数如表1所示。考虑加工制造的方便性及控制器的通用性,本文选择三相12/10-极FSPMM作为机械压力机的伺服直驱电机。其结构尺寸参数如图3所示。
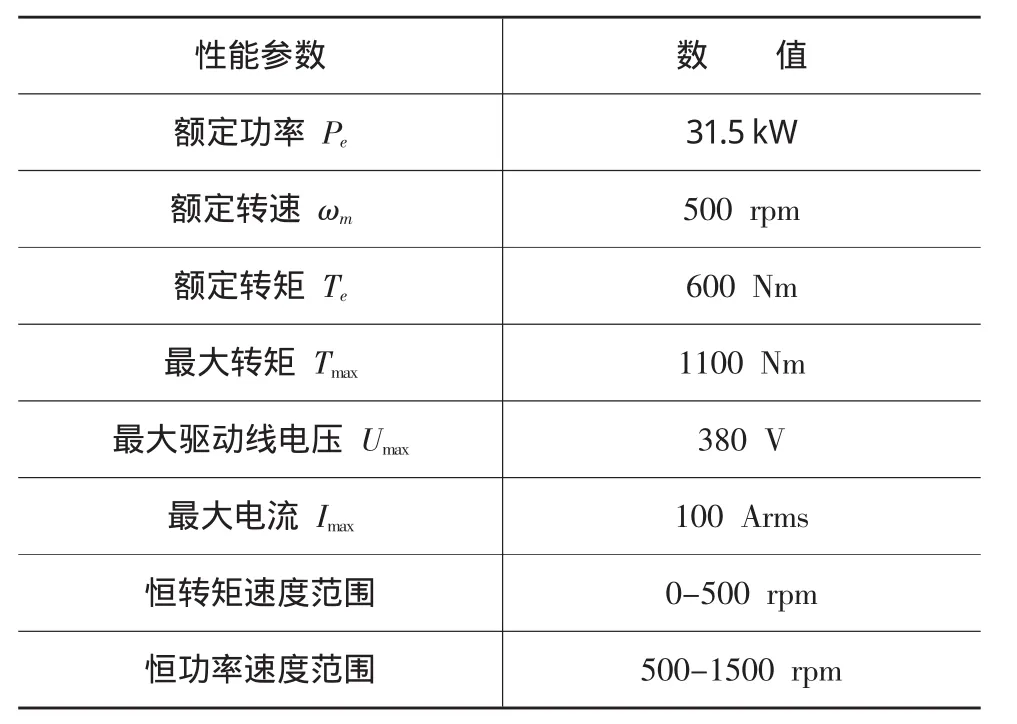
表1 FSPMM输出性能参数
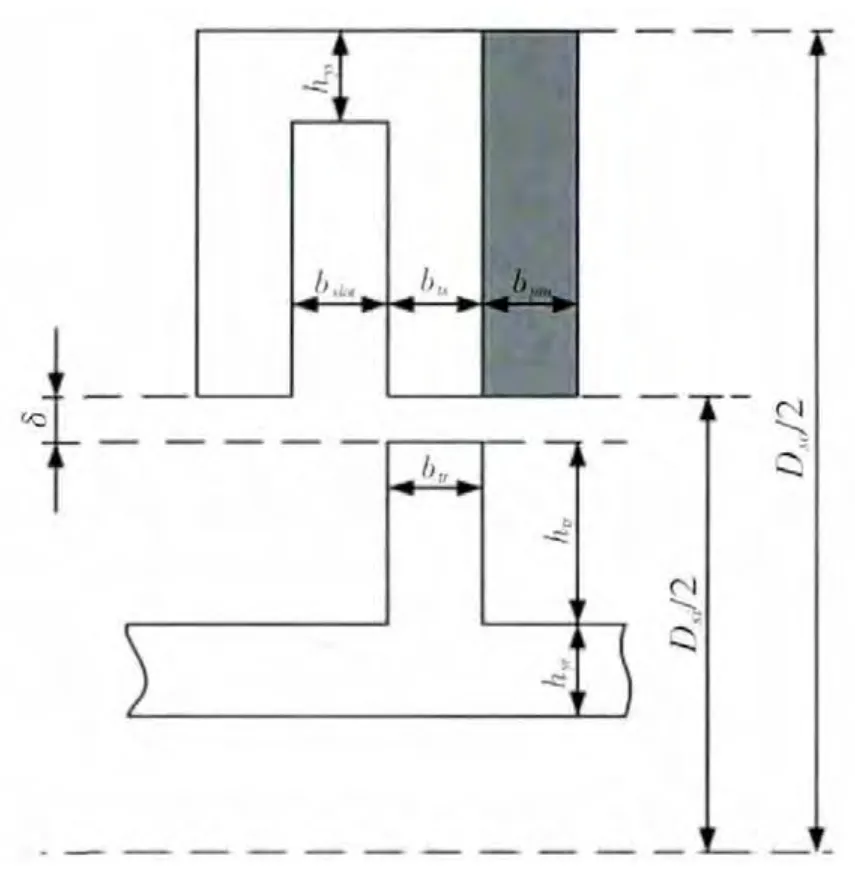
图3 FSPMM主要尺寸参数
由电机输出功率Po为:

式中:m——FSPMM电机相数;
Nk——各相总匝数;
E10——单匝线圈的空载反电动势;
Ik——FSPMM电机相电流;
Te——输出电磁转矩;
ωm——FSPMM额定角速度。
单匝线圈的空载反电动势E10可由下式求得:

式中:pr——FSPMM转子极对数;
øpeak——单匝线圈最大匝链磁通。
øpeak可由下式求得:

式中:Bt——定子铁芯磁通密度,由经验预估得Bt=1.6T;
ps——定子极数;
cs——定子齿宽系数,一般取为0.25;
La——定子轴向长度。
各相绕组输入安匝数NkIk可由下式表示为:
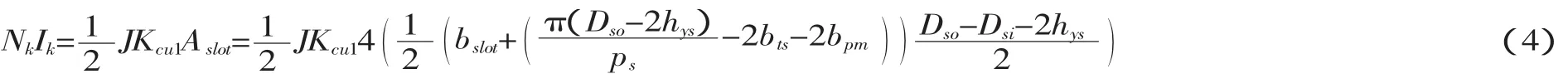
式中:J——输入电流密度,本文取 J=5×106A/m2;
Kcu1——槽满率,本文取Kcu1=0.5。
为同时满足磁负荷和电负荷需求,一般选择bslot=bts=btr=bpm=hys=hyr,即:
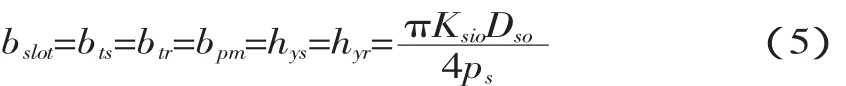
另外,转子齿高设置为:
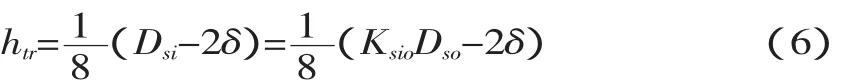
式中:Ksio——定子铁芯内外径比Dso/Dsi;
δ——气隙长度。
根据表1设定的FSPMM输出性能指标及限制外径尺寸 Dso=500mm,Ksio=0.65,联立式(1)~(4),求得 La≈120mm。由式(5)~(6)确定FSPMM 的其余尺寸,从而完成FSPM的初步设计,获得电机初始结构尺寸及参数,如表2所示。
3 基于有限元分析的FSPMM响应曲面优化设计
在确定FSPMM外形尺寸Dso、La的情况下,需要对其他影响FSPMM输出性能的尺寸参数进行优化。本文采用电磁场有限元分析方法获得不同尺寸参数下的电机输出性能参数,并利用响应曲面分析法进行尺寸参数优化。
3.1 FSPMM电磁场有限元分析
根据表2的FSPMM初始结构尺寸及参数在Ansoft Maxwell中建立电磁场有限元分析模型,并确定FSPMM各部分材料:电机转子由10#钢制成整体铁芯模块,电机定子铁芯由12个沿周向排列的U形铁芯单元组成,由冷轧硅钢片DW350-50叠压而成,永磁体采用钕铁硼材料,牌号为N35SH。然后进行瞬态场求解。观察FSPMM模型在转子齿分别与A相绕组所在的铁芯齿和永磁体对齐时的磁场分布,如图4所示。
由图可知,当转子磁极与集中绕组所缠绕的其中一个齿对齐时,该相绕组匝链磁通最大,当转子磁极与绕组所缠绕的永磁体对齐时,该相绕组的匝链磁通为0,当转子磁极与绕组所缠绕的另一个齿对齐时,该相绕组的匝链磁通最大,且方向转变。
3.2 FSPMM响应曲面优化设计
在 FSPMM 各尺寸参数中,Ksio、bts、btr、bpm的改变均对磁场分布造成影响,为使磁通回路一致,一般设定hys=hyr=bts。保持bslot不变,改变bpm的同时也使bts发生反向变化,另外在Dso确定情况下,内外径比Ksio的大小决定了永磁体的用量和输入绕组电流安匝数,因此本文以研究三个尺寸参数Ksio、btr、bpm对FSPMM输出转矩Te、转矩脉动Trip的影响,以输出转矩大小满足驱动要求为约束条件,转矩脉动最小化为优化目标进行优化。
利用响应面分析法设定因子采样样本尺寸,通过电磁场有限元分析获得样本结果,建立响应曲面数学模型,设定优化目标完成尺寸优化设计[11]。表3所示为利用中心复合序贯(CCC)设计RSM模型的样本集,在Ansoft中分别建立有限元模型进行瞬态场分析,获得各样本尺寸下的输出转矩Te和转矩脉动Trip。并以此建立其3因子二次RSM数学模型如下:

表3 CCC试验设计的3个因子的变化范围/mm
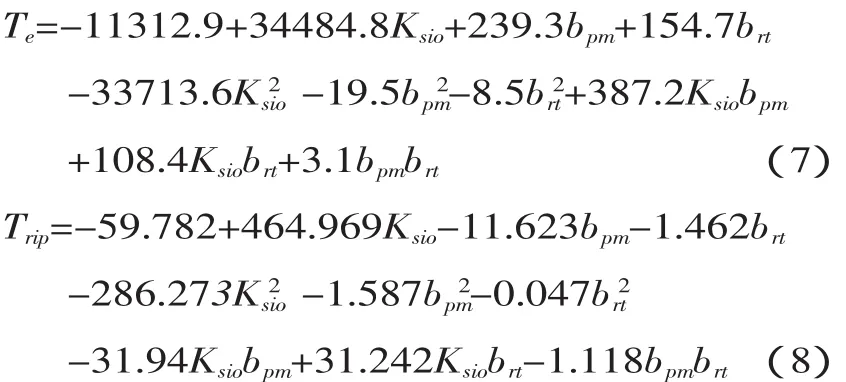
采用多重相关系数R2和修正后的多重相关系数Ra2检验RSM模型的拟合程度,得到输出转矩的R2为96.60%,Ra2为90.48%;转矩密度的R2为99.37%,Ra2为98.24%;转矩脉动的R2为92.89%,Ra2为90.10%,说明RSM的二次模型具有很高的拟合度。
利用RSM模型进行优化,首先对优化目标进行设置,确定输出转矩必须满足驱动主轴转矩大小,同时降低转矩脉动,保证转矩输出的稳定性。RSM的因子优化结果如图5所示。
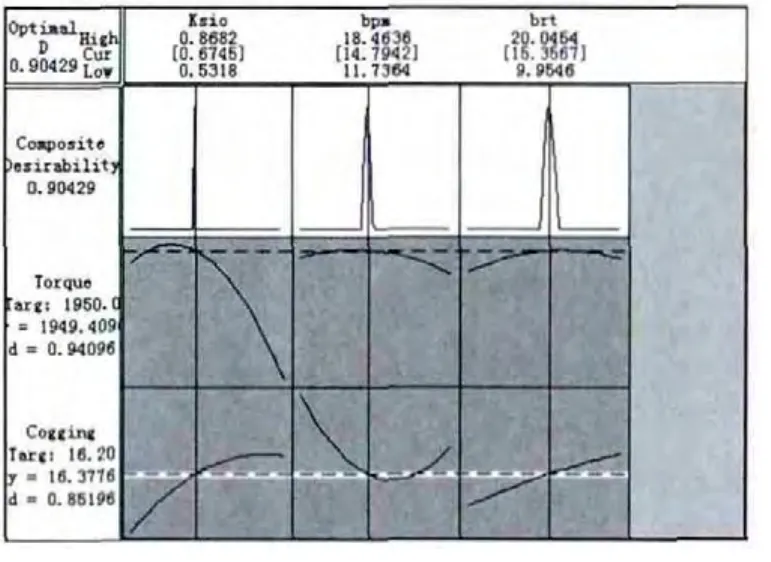
图5 响应面优化结果示意图
优化得到3个因子的优化解为:Ksio=0.6745,bpm=14.7942mm,btr=15.3567mm。优化后的输出转矩达到635Nm,转矩脉动降低为32.7552Nm,为输出转矩5.35%,满足主轴驱动的要求。为使得零件加工方便,最终确定优化因子取值为:Ksio=0.675、bpm=14.8mm、btr=15.4mm。
利用优化后的尺寸值建立有限元模型,求解FSPMM的输出性能参数,得到FSPMM的各相匝链磁通波形,各相反电动势波形,自定位转矩波形,输出电磁转矩波形,如图6所示。可见优化后的FSPMM满足表1中驱动压力机的性能要求。
4 结论
本文提出了一种用于伺服直驱机械压力机的开关磁通永磁电机的设计与优化方法,首先根据压力机伺服直驱要求确定电机性能参数并由理论计算获得电机初始结构尺寸及电磁参数,在此基础上利用有限元法分析电机性能,并结合响应曲面分析法对电机进行优化,从而获得满足压力机驱动要求的开关磁通永磁电机。在下一步的研究中,可根据优化后的电机参数制造样机,并用于驱动压力机,验证其伺服直驱的压力机运行性能是否得到提高。
[1] 赵升吨,何予鹏,王 军,邹 军.机械压力机低速锻冲急回机构运动特性的研究[J].锻压设备与制造技术,2004,39(3):24-32.
[2] 尚万峰,赵升吨.伺服压力机加工工艺的Bezier模型及其优化研究[J].西安交通大学学报,2012,46(3):34-38.
[3] 谢 嘉,赵升吨,沙郑辉.用于机械压力机驱动的电动机发展趋势探讨[J].锻压装备与制造技术,2009,(6):13-17.
[4] 赵婷婷,贾明全,姜则东.新型开关磁阻伺服压力机传动系统设计[J].锻压技术.2008,33(1):112-115.
[5]尚万峰.开关磁阻电动机伺服直驱机械压力机的关键技术研究[D].西安:西安交通大学,2009.
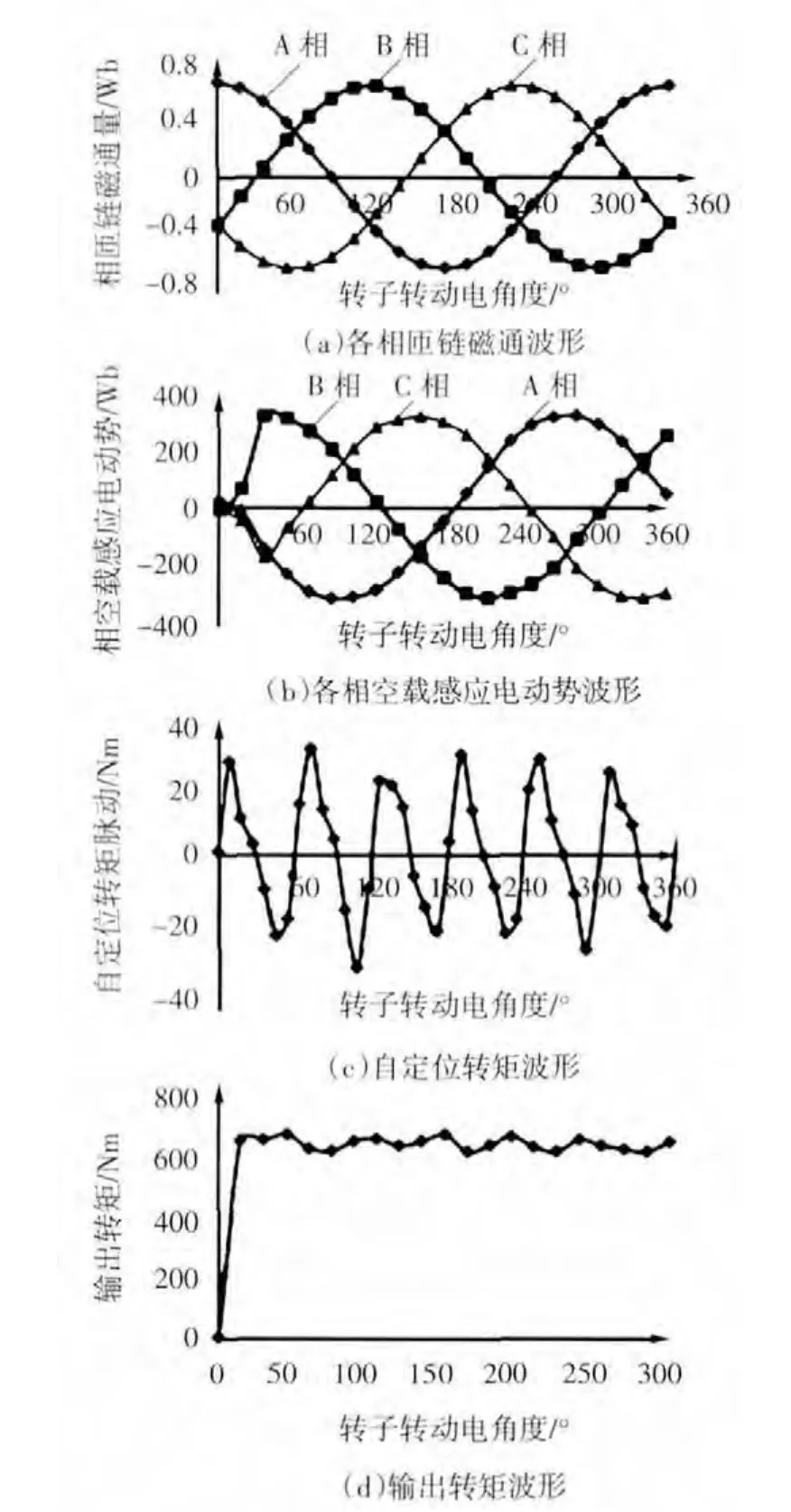
图6 优化后的FSPMM输出性能的有限元计算结果
[6] 尚万峰,邵丽红,赵升吨.SRM直驱伺服压力机的柔性控制建模与带负载仿真[J].锻压技术,2011,(5):57-62.
[7]Z.Q.Zhu,Y.Pang D.Howe,S.Iwasaki,R.Deodhar,and A.Pride.Analysis of electromagnetic performance of flux-switching PM machines by non-linear adaptive lumped parameter magnetic circuit model[J].IEEE Transactions on Magnetics,2005,41(11):4277-4287.
[8] W.Hua,Z.Q.Zhu,and D.Howe.Analysis and Optimization of Back EMF Waveform of a Flux-Switching Permanent Magnet Motor[J].IEEE Transactions on Energy Conversion,2008,23(3):727-733.
[9] Z.Q.Zhu,and J.T.Chen.Advanced Flux-Switching Permanent Magnet Brushless Machines[J].IEEE Transactions on Magnetics,2005,46(6):1447-1453.M.Aydin,S.Huang,T.A.Lipo.Axial Flux Permanent Magnet Disc Machines:a review[C].IEEE International Electric Machines and Drives Conference,2001,645-651.
[10]压力机杆系优化求解的变量循序组合响应面法[J].西安交通大学学报,2012,46(5):232-238.
[11] D.K.Hong,B.C.Woo,D.H.Kang.Application of fractional factorial design for improving performance of 60W transverse flux linear motor[J].Journal of Applied Physics,2008,103(7):1-3.
- 锻压装备与制造技术的其它文章
- 曲柄压力机电机-飞轮系统设计计算
- 基于有限元的大吨位压力机立柱结构改进

