Ne原子与HF分子碰撞振转激发分波截面的研究*

徐 梅 王晓璐 令狐荣锋 杨向东

1)(贵州师范大学物理与电子科学学院，贵阳 550001)

2)(贵州师范学院物理与电子科学学院，贵阳 550018)

3)(四川大学原子与分子物理研究所，成都 610065)

(2012年3月18日收到;2012年11月8日收到修改稿)

1 引言

原子与分子的碰撞过程和相互作用，是原子与分子物理学中非常重要的研究内容.原子分子碰撞提供的各种原子分子的科学数据，在能源、环境、医学、材料和生命科学以及国防研究中都发挥着重要的作用，在开拓高新技术产业、推动科技发展等方面有着不可忽视的重要地位.原子与分子相互作用势在理论计算中非常重要，因为一旦确定了精确势能面，原则上所有可观测的物理量均可计算.因此许多实验和理论工作者都致力于原子与分子系统相互作用势能面的研究，这方面的工作一直在不断地创新和发展[1-10].例如，HF分子泛频激光具有较好的大气传输性能和高亮度特征[11,12]，因而成为强激光体系的重要候选对象;而稀有气体对HF分子具有弛豫作用[13-15]，在改善HF激光的大气传输性能方面有着广泛用途;另外用HF的水溶液氢氟酸生产的氟化盐被广泛地应用于食品保护、特种金属冶炼、皮革和纺织品处理、标本保存以及核工业等行业.但是HF是一种不好打交道的化学试剂，它的强腐蚀性对实验设备损害非常严重，因此从理论上研究稀有气体Ne-HF的振转非弹性碰撞激发过程有着重要的意义.

本文采用单双取代并加入三重激发项校正的二次组态相互作用QCISD(T)方法，在aug-cc-pVTZ基组水平上对Ne与HF分子间的相互作用势进行了计算.并考虑了Boys和Bernardi提出的均衡法(counterpoise method，CM)在计算的基础上消除基组重叠误差(BSSE).计算得到了Ne原子与HF分子碰撞系统的相互作用势在 0°，20°，40°，60°，80°，90°，100°，120°，140°，160°，180°共 11 个方向上，步长取0.01，在2.0—10.0范围内的891个势能点数据.接着在Legendre多项式里展开势能表面，进行矩阵变换，使用Huxley势函数对数据点进行非线性最小二乘法拟合，计算了各向异性势的径向系数 V0，V1，V2，V3等，其函数形式能够很好地描述 Ne原子与HF分子碰撞系统的势能面.在此基础上，采用密耦近似计算得到了Ne原子与HF分子碰撞系统不同能量下的总截面、弹性分波截面、非弹性分波截面.

2 研究的主要理论和方法

式中，E表示碰撞系统的总能量，R表示入射原子Ne与耙分子HF质心的相对距离，r表示分子的核间距离，(+)表示外向边界条件，α表示一组完整的入射通道量子数.系统的总哈密顿为

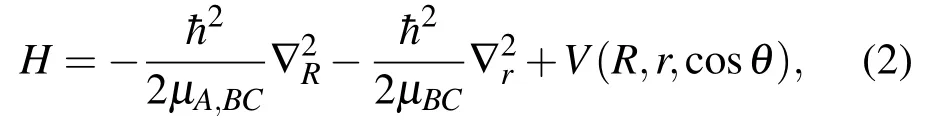
如图 1所示，式中，cosθ=R·r，µNe,HF表示系统的总约化质量，µHF表示HF分子的约化质量，V(R,r,cosθ)是碰撞系统的相互作用势.

图1 Ne原子与HF分子碰撞的几何图形

式中α为入射通道，γ为γ通道相应的量子数，knαJα可以简写为kα，φ(r)为双子分子振转波函数的径向部分，g(R)为原子相对分子质心运动的径向波函数，Y(R,r)为原子围绕分子转动和靶分子中原子转动的总角函数，n为振动量子数，J为系统的总角动量，lγ表示γ通道中原子绕分子转动的量子数，Jγ为γ通道中靶分子转动的量子数.

3 Ne与HF分子间的相互作用势研究

3.1 HF分子的振转能级

根据波恩近似，可将分子的几种主要运动状态同一定的能量相互联系起来，分子的总能量则由对应的质心平动能E，电子能Ee，振动能Ev和转动能Er共同求和得到，即

式中，质心平动能E的改变不会引起分子内部状态的变化，而另外三项Ee，Ev，Er的能量大小有：Ee∼102Ev，Ev∼102Er，所以在考虑的碰撞能量下，通常不会涉及到电子状态的变化情况，仅可能产生振转激发.根据经过微扰理论验证的Herzberg的振转能级规律表达式[16]，双原子分子的振动光谱项为

式中，ωe表示谐振频率，ωeχe表示非谐振频率，Be表示刚性转动常数，De表示转动离心常数，αe表示非刚性转动常数，v表示振动量子数，J表示转动量子数.

双原子分子HF的光谱常数如表1所示[17].

表1 HF分子的光谱常数(单位：cm-1)

根据表1和方程(10)式，即可计算得到HF分子的振转能级的差值，如表2所示.

表2 HF分子振转能级值(单位：eV)

3.2 HF的势能函数

采用Murrell-Sorbie[18]函数，对Rydberg[19]提出的势能函数

经过修正，得到函数：

其中参量a1，a2和a3可由下列公式确定：

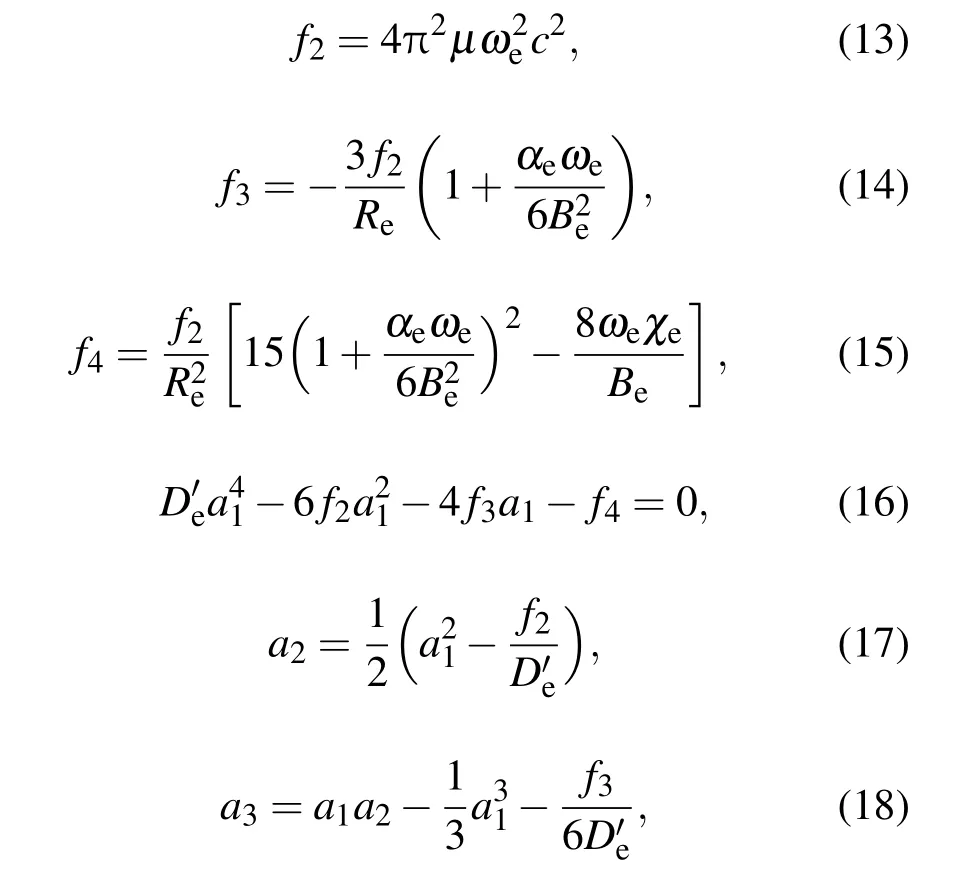
式中µ为双原子分子的约化质量，c是光速，ωe，ωeχe，Be，αe，De为光谱常数.

因此，根据表1和(13)到(18)式，可以计算得到基态HF分子的Murrell-Sorbie势能函数的参量和力常数，如表3所示.

表3 HF分子势能函数参量及力常数

表3的计算结果与文献[20]完全一致.

3.3 Ne原子与HF分子碰撞系统的相互作用势

采用QCISD(T)方法，在aug-cc-pVTZ基组水平上，分别对Ne与HF分子间相互作用势进行系统研究，r取优化值0.916808.

运用Boys和Bernardi提出的CM法[21]，为了提高计算的精确性，在计算的基础上消除基组重叠误差(BSSE).

在 θ =0°，20°，40°，60°，80°，90°，100°，120°，140°，160°，180°共 11 个方向上的势能曲线如图 2所示.

研究原子与双原子分子的碰撞，我们需要得出体系的球对称势和各项异性势的表达式，一般情况下，碰撞体系的相互作用势V(R,r,θ)可写成：

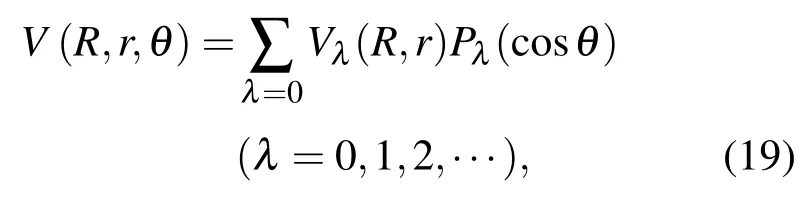
其中Vλ(R,r)为径向势函数，Pλ(cosθ)为 Legendre函数，θ为原子相对于双原子分子的方向角.

图2 Ne-HF的势能曲线

V0(R,r)称为球对称势，V1(R,r)，V2(R,r)，V3(R,r)，V4(R,r)等也称为各向异性势径向系数，表征各向异性势的特征.V(R,r,θ)用矩阵可表示为

将上式左乘 P-1，即得：Vλ(R,r)=P-1V(R,r,θi).

使用Huxley势函数对Ne原子与HF分子碰撞系统的径向系数点进行非线性最小二乘法拟合，拟合公式为

式中，拟合参数为：A，Re，a1，a2，a3，a4，C6，C8，C10.前七个径向系数 Vn(R,r)(n=0，1，2，3，4，5，6)随 R的变化关系如图3所示.

图3 Ne-HF拟合势的径向系数

3.4 Ne原子与HF分子碰撞截面的计算

由于HF的高腐蚀性和实验的难度，Ne原子与HF分子碰撞的分波截面实验数据一直未见报道，也未见其他理论数据报道.因此，本文旨在为这方面的工作做一点探索，提供一定的参考.

图4 Ne-HF碰撞系统分波截面(E=50 meV)

图4和图5分别是入射能量为50 meV和100 meV时，Ne原子与HF分子碰撞系统的分波截面随量子数J的变化曲线.其中包括碰撞系统的TCS总截面，弹性00-00分波截面，以及00-01，00-02，00-03等相应系统的非弹性碰撞激发分波截面.

图5 Ne-HF碰撞系统分波截面(E=100 meV)

图4和图5右上角的小图为非弹性分波截面00-02，00-03等的坐标缩放图.从图中可以看出Ne-HF碰撞系统在50 meV与100 meV时，总截面和弹性00-00截面出现一个极大值后，尾部出现很强的尾部效应，然后迅速收敛.这是由于在最靠近R的远距离处，势的尾部有很强的吸引支产生的，弹性00-00截面对总截面的贡献是最大的.50 meV的低转动跃迁00→01和100 meV的00→01，00→02有两个峰值，说明低激发态产生尾部效应，高激发态不产生尾部效应.由于非弹性截面也有比较强的尾部效应，所以总截面的尾部效应较高.另外，随着能量的升高，分波截面的振荡次数增多，极大值变小，振荡极大值的位置也向J增大的方向发生移动.尾部效应相对变弱.产生非弹性激发跃迁的几率将增大，因此，弹性分波截面极大值变小，并且极大值位置向J增加的方向移动，分波截面的振荡次数增加，收敛速度变慢.

4 结论

本文采用单双取代并加入三重激发项校正的二次组态相互作用(QCISD(T))方法，以及aug-ccpVTZ基组对He-HF分子间相互作用势进行了计算，为了提高计算得到的相互作用势离散点数据的精确性，我们考虑Boys和Bernardi提出的均衡法在计算的基础上消除基组重叠误差.计算得到了Ne与HF分子碰撞系统的相互作用势在0°，20°，40°，60°，80°，90°，100°，120°，140°，160°，180°共 11个方向上，步长取0.01，在2.0—10.0范围内，每个系统的891个势能点数据.接着在Legendre多项式里展开势能表面，进行矩阵变换，得到各向异性势的径向系数 V0，V1，V2，···.最终确定使用拟合效果较好，物理意义也比较明确的Huxley势函数，对11个方向的径向系数点进行非线性最小二乘法拟合，其函数形式能够很好地描述Ne原子与HF分子碰撞系统的势能面.

经过与可查询的散射截面的实验值进行了细致的对比，检验了拟合势的可靠性和散射截面密偶计算结果的可靠性.结果显示：我们构造的势模型不仅表达形式较为简洁，而且能够很好地描述Ne-HF分子碰撞系统的散射截面.曾计算的微分散射截面的衍射振荡位置和振荡幅度与实验光谱测量值具有相同的变化规律，而且符合得很好.因此，我们的拟合势能够很好地反映Ne-HF分子碰撞系统的相互作用特征，计算的碰撞激发分波截面的结果是可靠的.

[1]Scole G 1988 Atomic and Molecular Beam Methds(Oxford：Oxford University)

[2]Yu C R，Zhang J，Jiang G S 2009 Acta Phys.Sin.58 2376(in Chinese)(in Chinese)[余春日，张杰，江贵生2009物理学报58 2376]

[3]Huang D H，Wang F H 2009 Acta Phys.Sin.58 6091(in Chinese)[黄多辉，王藩侯2009物理学报58 6091]

[6]Shen G X，Linghu R F，Wang R K，Yang X D 2007 Chin.Phys.16 3352

[7]Wang R K，Shen G X，Song X S，Linghu R F，Yang X D 2008 Acta Phys.Sin.57 4138(in Chinese)[汪荣凯，沈光先，宋晓书，令狐荣锋，杨向东2008物理学报57 4138]

[8]Wang X L，Linghu R F，Yang J H，LB，GaoT，Yang X D 2012 Acta Phys.Sin.61 093101(in Chinese)[王晓璐，令狐荣锋，杨建会，吕兵，高涛，杨向东2012物理学报61 093101]

[9]Shen G X，Wang R K，Linghu R F，Yang X D 2011 Acta Phys.Sin.60 013101(in Chinese)[沈光先，汪荣凯，令狐荣锋，杨向东2011物理学报60 013101]

[10]Shen G X，Linghu R F，Wang R K，Yang X D 2007 Chin.Phys.16 3352

[11]Miller J 1987 AIP Con.Proc.160 10

[12]Smith J H，Robinson D W 1981 J.Chem.Phys.74 5111

[13]Taatjes C A，Leone S R 1988 J.Chem.Phys.89 302

[14]Cuellar E，Parker J H，PrimatelG C 1974 J.Chem.Phys.61 422423

[15]Jiang G，Xie H P，Zhu Z H，Cheng H D，Yang W D，Liu D Y 1998 Chin.J.Lasers 25 817(in Chinese)[蒋刚，谢洪平，朱正和，陈涵德，杨卫东，刘冬燕1998中国激光25 817821]

[16]Herzberg G(Translated by Wang D C)1983 Molecular Spectrum and Molecular Structure(Beijing：Science Press)(in Chinese)[Herzberg G著，王鼎昌译1983分子光谱与分子结构(北京：科学出版社)]

[17]Huber K P，Herzberg G 1979 Molecular Spectrum and Molecular Structure(IV)Constants of Diatomic Molecules(New York：Van Nostrand Reinhold Company)

[18]Huxley P，MurrellJ N，Sorbie K S 1983 Chem.Soc.Faraday Trans.II 79 323

[19]Rydberg Z R 1931 Physica 73 376

[20]Zhu Z H，Yu H G 1997 Molecular Structure and PotentialEnergy Function(Beijing：Science Press)(in Chinese)[朱正和，俞华根 1997分子结构与分子势能函数(北京：科学出版社)]

[21]Boys S F，BernadiF 1970 Mol.Phys.19 533