上海光源软X射线干涉光刻线站波荡器光源及束线相干性研究
郭春磊 孟祥雨 吴衍青 王 勇 邰仁忠
(中国科学院上海应用物理研究所 嘉定园区 上海 201800)
上海光源软X射线干涉光刻线站波荡器光源及束线相干性研究
郭春磊 孟祥雨 吴衍青 王 勇 邰仁忠
(中国科学院上海应用物理研究所 嘉定园区 上海 201800)
同步辐射波荡器光源相干性能逐步提高,使得同步辐射相干光学实验对理论模拟的要求越来越高。对同步辐射光束线空间相干性进行有效的评估,可以指导相干光束线的设计及其相干光学实验的开展。本文利用部分相干光传播计算模型,数值模拟了上海光源软X射线干涉光刻光束线部分相干光的传播,理论和实验结果进行了比较,得到不同参数下的空间相干性,分析了误差产生原因。相干性的定量分析结果可以为实现空间相干性的定量控制提供依据。
X射线光学,空间相干性,波荡器,相干长度
随着第三代同步辐射装置发射度、亮度等关键性能指标的提高以及X射线自由电子激光装置(XFEL)的发展,各种同步辐射相干光学实验方法的应用越来越普遍,如相干衍射成像(CDI)技术[1]、X射线干涉光刻(XIL)技术[2];如Spring8同步装置上的BL29XU这样的相干光学光束线也越来越多。上海光源具有多个高相干性线站,如软X射线干涉光刻线站(BL08U1B),目前BL08U1B线站可以进行XIL实验,制备大面积纳米周期模板。在这样的光束线中,准确的空间相干性的评估是保证实验顺利进行的基本条件。
第三代同步辐射波荡器光源具有较好的空间相干性[3]。对于部分相干光的描述采用统计光学中交叉谱密度的概念。分析部分相干性所采用的理论模型主要有高斯谢尔模型(GSM)和在此基础上建立的相干模式分解模型(CMD)。采用上述理论模型后,可以得到交叉谱密度的解析形式,在硬X射线波段(光子能量范围大于3 keV)范围内应用广泛。但是GSM和CMD并不适用于软X射线波段[4−6],所以本文通过直接计算波荡器光源辐射场获得交叉谱密度、相干度和相干长度。这样,波荡器光源的部分相干性的描述更加精确,更具有一般性。
目前基于波动光学的同步辐射光束线模拟程序不多,如SRW[7,8]、PHASE[9],它们适用于XFEL飞秒脉冲波前传播,考虑了光学元件对脉冲等相面的影响,进而引起光强分布的变化,最终影响光束线的波前性质。但是针对第三代光源光束线的空间部分相干光模拟软件未见报道。
本文分以下几个部分:(1) 介绍用于光束线的相干性分析的数值计算模型,以及在此模型基础上编写的程序MCI;介绍本文使用的理论计算模型,用于计算不同位置处的光源相干长度;介绍BL08U1B光束线的光学布局。(2) 利用MCI分析波荡器谱宽对衍射图样的影响;利用MCI模拟出射狭缝的衍射图样,并与实验测得的衍射图样对比,确定次级光源(出射狭缝)处的相干长度;理论计算结果与模拟结果对比,并作了误差分析。
1 数值计算模型、理论模型及光束线主要参数
1.1数值计算模型
本文使用的数值计算模型是在已有的互强度传播模型的基础上做了进一步近似,使之能够快速计算像平面上的互强度分布,得到该像平面上的相干长度。原理如下:互强度的传播满足赫姆霍兹方程:
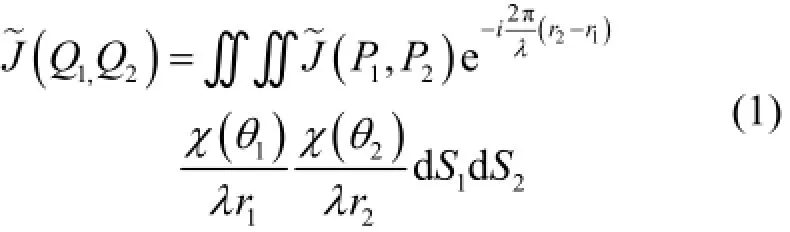
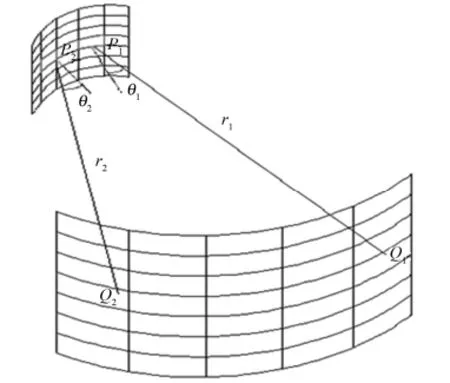
图1 自由空间中互强度的传播Fig.1 Sketch of the propagation of mutual optics intensity in free space.
式(1)描述了计算像平面上互强度分布的解析公式。但是对于X射线来说,由于其波长相对于可见光来说很短,式(1)是无法用解析的方法计算出来的。本文采取将波前合理分割成很多平面小面元的近似方法,在每个小面元内式(1)的积分可以用解析的方法计算出来,然后将每个小面元的结果叠加,就可以得出整个波前的计算结果。
目前程序MCI已能模拟同步辐射部分相干光在自由空间的传播,可以描述通过狭缝后的互强度变化,并已得到初步验证[10];通过改变强度分布标准差σ1和归一化互强度的模(相干系数)的分布的标准差σ2得到具有不同相干性的面光源,其中σ1描述了光强的分布,同样大小的光源,σ1值越大,光强分布就越均匀;σ2描述了相干系数的分布,当相干系数满足高斯分布时,相干长度Lc=1.772σ2;所以,相同光束尺寸下,σ2值越大,光源的相干性就越好。
1.2同步辐射空间相干性分析的理论模型
在分析波荡器光源的相干性时可以把波荡器光源等效成一个位于波荡器中心横截面的面光源[11,12],面光源处的相干长度由相干度定义。同步辐射的电场部分由两部分构成,称为“近场”和“远场”,计算“远场”可以得到简洁的解析形式,通常计算辐射的亮度时采用“远场”近似。但是在考虑同步辐射的空间相干性时,必须要从具体的光源点(面)出发,推算光束线上的任意位置处的次级光源的相干性。并且绝大部分光束线中,距离波荡器最近的光学镜组只有20 m,所以不能用“远场”近似条件。从这一角度考虑,本文通过数值方法计算波荡器辐射场(包括近场和远场)。另外由于同步辐射单个X射线脉冲持续时间约为30 ps,而探测器的时间分辨极限约为100 ps,所以探测器分辨不出E(t)信号的时间结构,E(t)信号在时间上是稳定的,结合波荡器辐射准单色的特点,在频域中分析E(ω)信号较为有利。E(ω)是E(t)的傅里叶变换,即E(ω)=∫dtE(t)exp(iωt),ω为波荡器辐射电场的圆频率。
本文选择交叉谱密度[14−16]概念来描述同步辐射空间相干性,它就是某个频率成分的互强度。本文采用以下参量作为基本参量:物面上的电子的空间位置坐标(x, y);物面上电子的运动方向坐标(x', y')和像面上点的空间坐标(ξ, η)。由于垂直方向电子束团的尺寸和发散度都很小(表1),相干性好,所以本文只考虑水平方向。那么,像面水平坐标轴上任意两点Q1(ξ1,0)、Q2(ξ2,0)的交叉谱密度函数定义为:
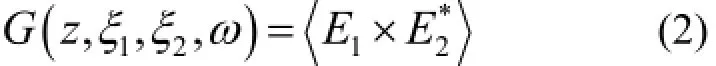
式中,z为像面到光源面的沿光轴的距离;其中:
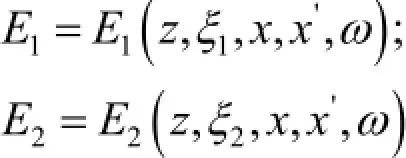
根据文献[13],尖括号<…>表示系综平均,在这里表示电子辐射场在电子水平相空间(x, x')内的概率密度分布的统计平均。电子在相空间的概率密度分布采用高斯分布,记做:
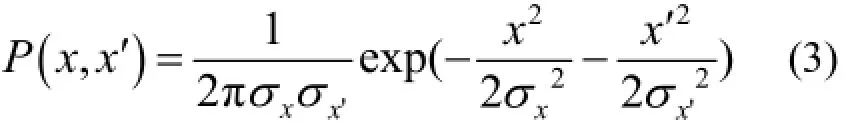
式中,σx表示电子位置高斯分布的标准差;σx'表示电子运动方向的发散度的标准差。所以z处像面上水平方向任意两点Q1(ξ1,0)、Q2(ξ2,0)的交叉谱密度可以写为:
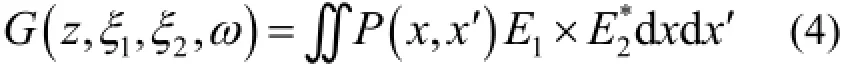
归一化的交叉谱密度即为相干度,Q1(ξ1,0)、Q2(ξ2,0)两点的相干度:
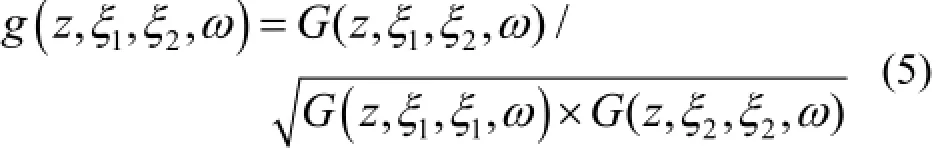
用相干长度的大小来表示相干性的好坏:
水平方向相干长度:
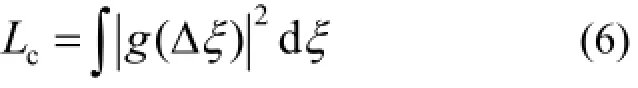
Δξ=ξ1−ξ2,BL08U1B、BL08U1B光束线采用EPU10波荡器,上海光源以及波荡器参数见表1。

表1 上海光源及EPU10参数Table1 Parameters of SSRF and EPU10.
利用式(2)−(6),计算光束线不同位置处横截面上的相干长度。用到的参数见表1,其中式(4)的积分范围分别取x∈[−3σx, 3σx], x'∈[−3σx', 3σx'],可以得到相干长度随传播距离的变化关系,如图2所示。结果显示,传播一定距离以后,相干长度随传播距离基本成线性关系。
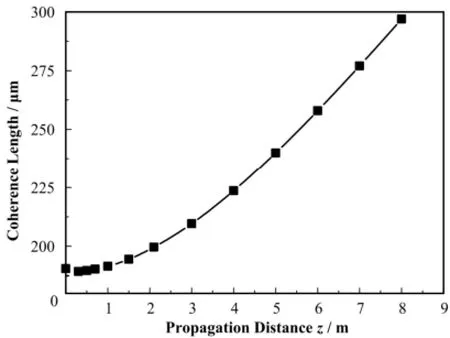
图2 相干长度随传播距离的变化Fig.2 Characterization of coherence length with different propagation distance.
1.3光束线光路布局
上海光源BL08U1B光束线水平方向光路图如图3所示。L1=22 m,L2=4 m,L3=4.6 m,同步辐射从波荡器出射以后自左至右先后经过水平聚焦镜M1、出射狭缝Slit。狭缝作为次级光源,可以根据不同实验需求调整狭缝大小,改变样品处的空间相干性。出射狭缝后4.6 m处安置丝扫描探针(BPM),用于测量狭缝后的光强分布,通过测量的衍射条纹的可见度,可以判断空间相干性的优劣。结合MCI程序模拟狭缝的衍射条纹,对比BPM所测条纹,当二者相符时可以得到狭缝处光斑的相干长度,由此可以定量地描述空间相干性的好坏。
2 SSRF-BL08U1B束线空间相干性分析
BL08U1B束线设计的主要思路是通过空间滤波裁剪出射狭缝处的次级光源,获得高空间相干性光束。次级光源的空间相干性对相干光学实验有直接影响,所以下面着重分析次级光源的空间相干性。与上文一致分析水平方向的空间相干性。
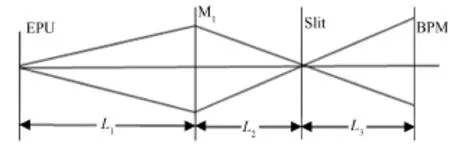
图3 上海光源08U1B光束线光路图Fig.3 Schematic setup of BL08U1B in SSRF.
2.1利用MCI分析波荡器辐射谱宽对空间相干性测量的影响
相干长度的测量是通过测量衍射条纹的可见度来实现的[17]。而谱宽将影响衍射条纹可见度,进而影响相干长度的测量。一定谱宽光源各频率成分的一级衍射峰不完全相同,从而使衍射峰展宽,峰值降低。BL08U1B的波荡器实际能谱图如图4所示。谱宽2.6 eV,相对谱宽Δλ/λ约为2.8%,假设谱宽对相干性测量的影响可以忽略。
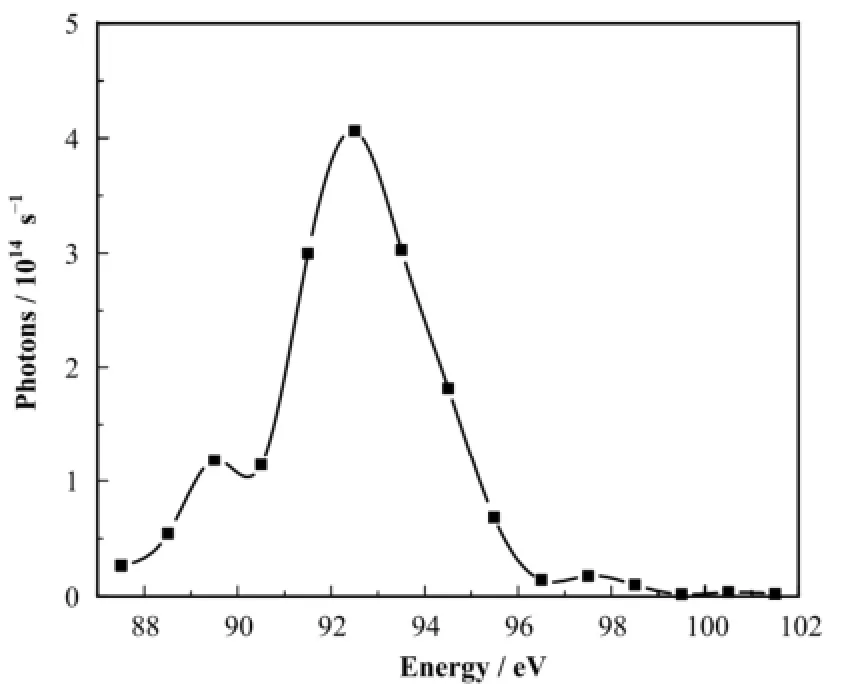
图4 基波光子能量92.5 eV时EPU能谱图Fig.4 EPU spectra for photon energy E=92.5 eV.
此处MCI可以进一步验证上述假设:首先通过BPM测量出射狭缝的衍射条纹(该衍射条纹是由一定频率成分的衍射场的光强叠加形成,由于通光条件下的光子通量在1014量级,挡光条件下杂散光的光子通量在109量级,所以杂散光对于该衍射条纹的影响可以忽略不计),然后结合MCI来获得出射狭缝处次级光源的相干长度。由于BPM在测量衍射场的水平方向的光强分布时,是在BPM丝的长度方向(垂直方向)的光强进行累加,所以利用MCI模拟水平方向的光强分布时,垂直方向的光强也要相应地进行累加。利用MCI分别模拟各频率成分的矩孔衍射。其中,波荡器实际能谱分布如图4所示,并假设光子能量92.5 eV(对应波长为13.5 nm)附近各频率成分空间相干长度相同。这里选取的实验条件为狭缝开口45 μm×45 μm。
按图4所示分别选取光子能量为89.5 eV、90.5eV、91.5 eV、92.5 eV、93.5 eV、94.5 eV,各频率成分的权重因子依次为0.08、0.08、0.21、0.29、0.21、0.13进行累加。多色光的光强分布图如图5(a)所示,多色光的光强累加衍射条纹与92.5 eV处单色光衍射条纹比较,结果如图5(b)所示,发现两者没有明显区别。
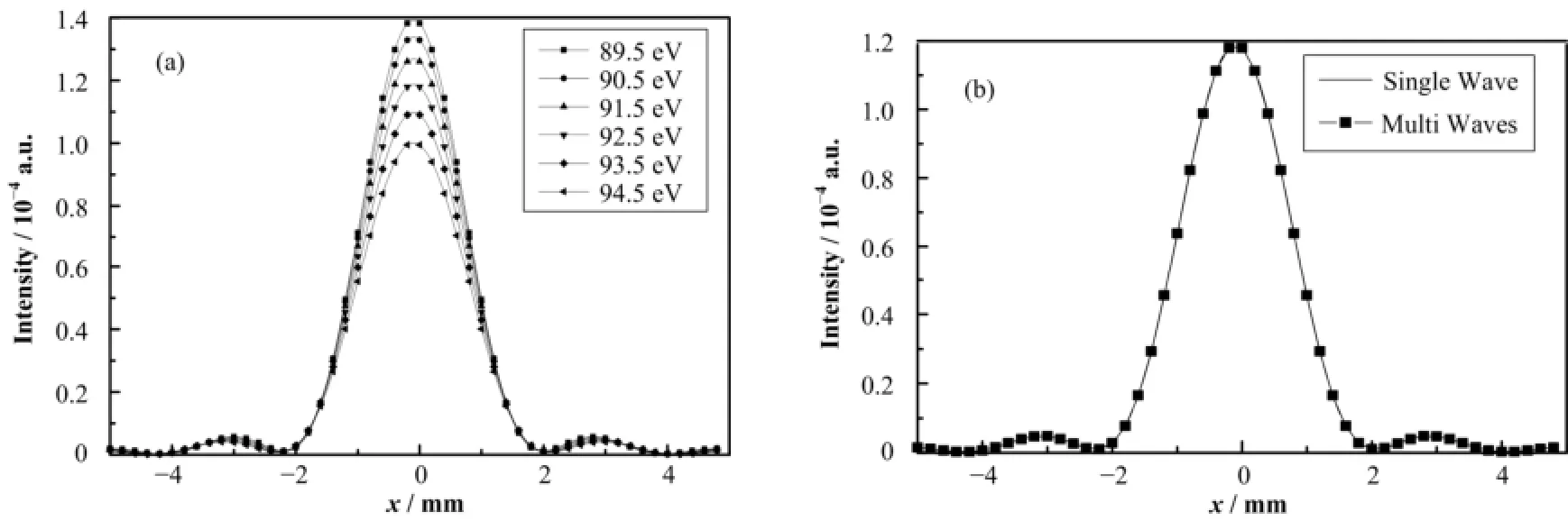
图5 不同能量的光强分布图(a)和波荡器谱宽对衍射条纹影响(b)Fig.5 Intensity distribution for different photon energy (a) and frequency bandwidth effect of undulator on diffraction fringe (b).
通过上述模拟,可以判定谱宽对于相干性测量的影响可以忽略的假设是成立的。所以,以下空间相干性评估中不再考虑谱宽的影响。
2.2次级光源空间相干性的实验测量及推算
狭缝开度45 μm×45 μm,物面和像面均分割成50×50个小面元,基波光子能量92.5 eV,对应波长13.5 nm,以水平方向为例。利用MCI模拟狭缝后4.6 m处的光强分布情况,按照零级峰归一化的光强在水平方向的分布情况,模拟相干系数σ2对衍射光强的影响,如图6所示。
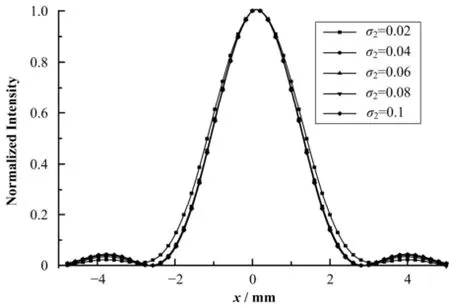
图6 MCI模拟光强分布,σ2的单位是mmFig.6 Distributions of intensity simulated by MCI and the unit of σ2 is mm.
σ2为0.02 mm时,由于相干长度很小,次级光源的空间相干性差,衍射条纹的相对光强小。随着σ2逐渐增大,相干长度增加,次级光源的空间相干性逐渐变好,一级衍射峰相对光强(I1/I0)逐渐增加。σ2对衍射条纹的影响可以通过一级和零级光强比值(I1/I0)随σ2的变化曲线反映出,如图7所示,I0为零级衍射光强;I1为一级衍射光强。当狭缝开口45 μm× 45 μm时,相干系数σ2大于0.1 mm时,比值(I1/I0)趋于稳定。
出射狭缝的衍射图样由BMP测得。实验测得的光强分布与MCI模拟结果符合较好时(图8),MCI中所采用的σ2=0.06 mm,所以狭缝处的水平方向相干长度Lc1=1.772σ2,约0.106 mm。由于BPM测量以及扫描精度所限,模拟图样与实际测量图样不能完全一致,在比较时主要考虑衍射峰相对强度一致。
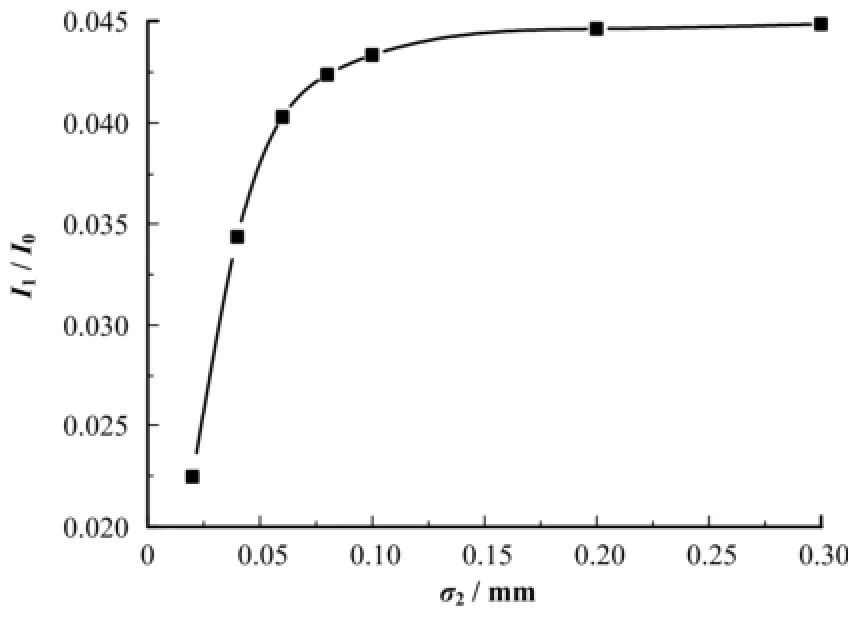
图7 σ2对(I1/I0)比值的影响Fig.7 Influence of σ2 on (I1/I0).
2.3次级光源空间相干性的理论计算和数值模拟
上海光源储存环参数如下:电子能量3.5 GeV;水平发射度3.9 nmrad;耦合系数0.01。采用的波荡器为椭圆极化波荡器,主要参数为:周期磁铁结构长度100 mm;周期数42;基波光子能量92.5 eV对应波长13.5 nm;偏转参数K=4.8117。面光源强度分布标准差为σx=158 μm;σy=9.9 μm。发散角标准差σx'=33 μrad;σy'=3.95 μrad。根据式(2)−(6)(其中式(4)的积分范围与上文一致分别取x∈[−3σx, 3σx],x'∈[−3σx', 3σx'])理论计算可得波荡器中心横截面的水平方向上相干长度Lc=0.19 mm,对应的相干系数高斯分布的标准差为σ2=0.107 mm,理论计算得到M1处相干长度为1.9 mm。
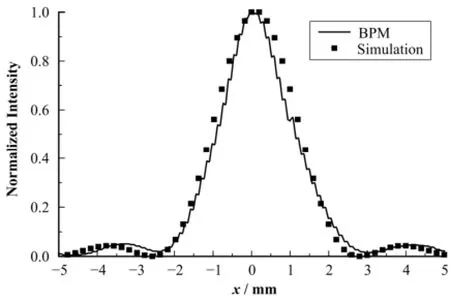
图8 BPM测得的衍射图与程序模拟图Fig.8 Diffraction figures detected by BPM and simulated by MCI.
以上理论计算结果σ2=0.107 mm和光源尺寸σx=158 μm作为MCI的初始参数。模拟部分相干光从波荡器到M1之间的传播。狭缝开度45 μm×45μm,物面和像面均分割成50×50个小面元,模拟结果如图9所示。模拟结果显示,从光源面传播至聚焦镜M1(22 m)处的光束在水平方向的尺寸为0.573 mm,相干系数σ2=0.864 mm,则相干长度Lc=1.772σ2约为1.53 mm。(MCI程序界面说明:界面上方图形为光强分布,Sigma=σ1分别为按照高斯分布拟合的水平和垂直方向的标准差;界面下方为相干系数分布,Sigma=σ2分别为按照高斯分布拟合的水平和垂直方向的标准差)。
现在考虑22 m处水平方向聚焦镜M1对光束空间相干性的的影响,等效的理想会聚透镜的位相因子为exp(−i×k(x2+y2)/2f),它对入射波位相进行了修正。据此修改程序以后可以模拟光束经过聚焦镜从M1(22 m)传播至狭缝Slit(26 m)时的情况,模拟结果如图9(b)所示。经过聚焦作用Slit(26 m)处的光束尺寸为0.022 mm (FWHM值为0.052 mm),相干系数σ2=0.071mm,相干长度为Lc2=1.772σ2约为0.126mm。
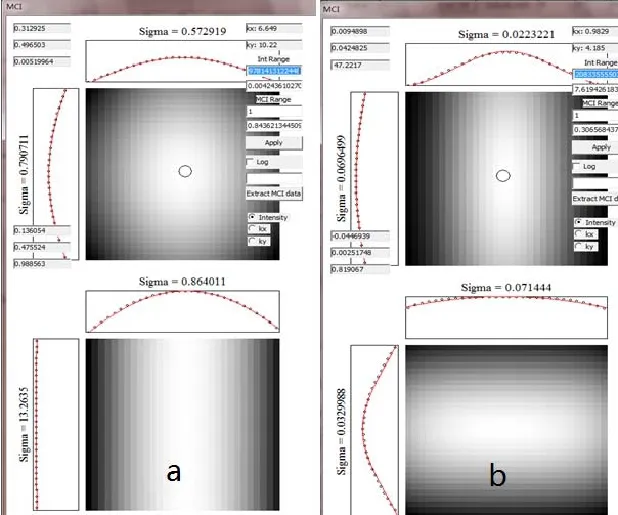
图9 程序模拟结果 (a) 自由空间传播至22 m处,(b) 通过聚焦作用从22 m处传播至26 m处Fig.9 Simulated results by MCI. (a) after 22 m propagation in free space, (b) propagate from 22 m to 26 m after focus
3 误差分析
实验部分:通过BPM测得的狭缝衍射条纹,利用MCI模拟该衍射过程,衍射条纹符合较好时,由MCI得到狭缝处的相干长度为Lc1=0.106 mm。理论计算部分:通过计算波荡器光源的相干系数的高斯分布的标准差σ2=0.107 mm,并以此作为MCI的初始参数,对部分相干光在光束线中的自由空间传播和经过聚焦镜的聚焦作用之后的传播进行模拟,得到狭缝处的相干长度为Lc2=0.126 mm。各处光束尺寸和相干长度列于表2。
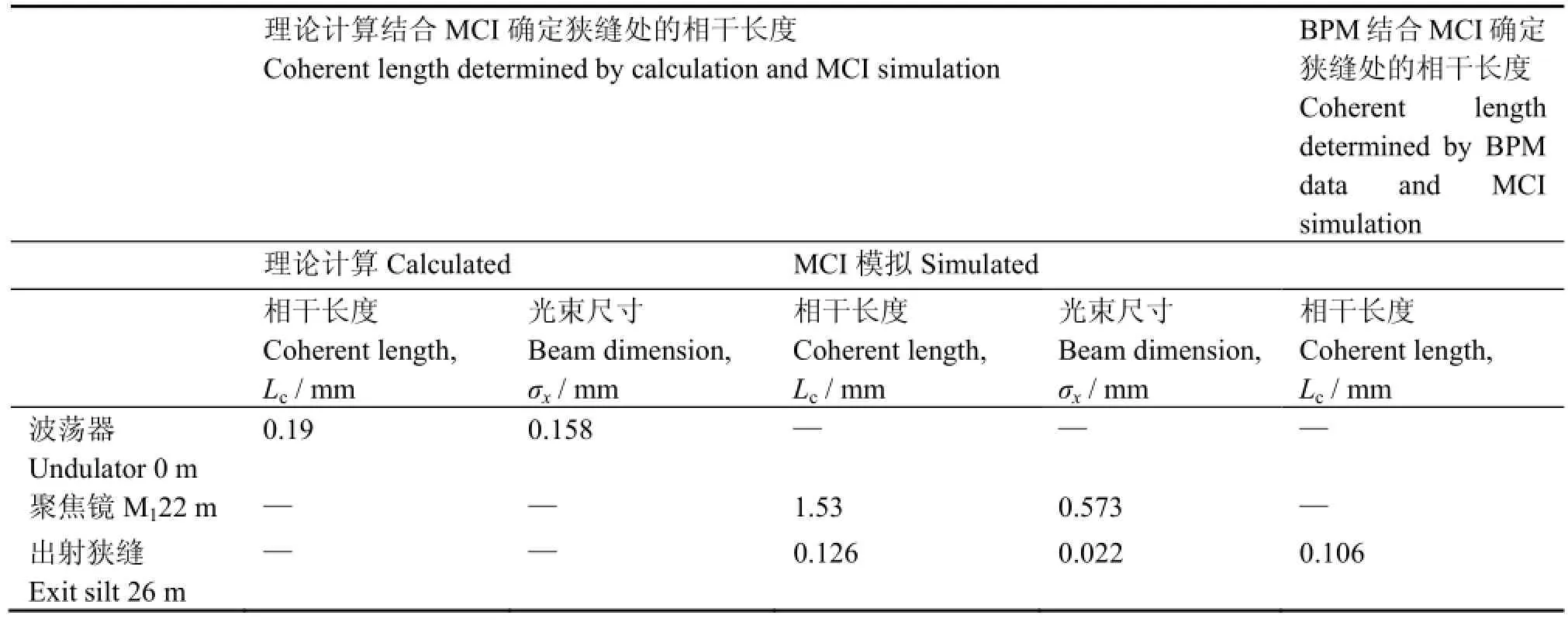
表2 计算结果和模拟结果Table2 Simulation and caculation results.
比较实验结果和理论结果,狭缝处的相干长度的理论结果(0.126 mm)比实验结果(0.106 mm)大;通常情况下,光学元件的缺陷(粗糙度、面型误差等)会降低光束的空间相干性[18]。除此之外,造成上述误差的主要原因还有实验测量误差:一方面由于BPM测量水平方向光强时,在垂直方向上是连续的光强积分,而MCI模拟时,则是有限点(50个点)的光强叠加,影响实验结果。另一方面,BPM的光强测量误差在5%以内,由图6,σ2对衍射光强分布的影响体现在一级和零级的相对光强大小,所以由于BPM测量误差造成对MCI中的σ2的影响。由图7可见,σ2真实值应该在0.05−0.08 mm,相干长度应为0.0886−0.142 mm。
另外,MCI在加入粗糙度和面型误差等因素之后,可以定量模拟光学元件的缺陷对相干性的影响,使得上述误差范围进一步精确。
4 结语
忽略波荡器光源计算所造成的误差,利用BPM结合MCI模拟结果所得到的相干长度在0.0886−0.142 mm,这与利用理论计算模型所得到的狭缝处的相干长度0.126 mm基本一致。说明利用上述方法分析光束线的空间相干性是可行的,所得结论不但有助于相干光束线的设计,还可以为相干光学实验中空间相干性的定量控制提供重要的理论参考。
1 Miao J W, Charalambous P, Kirz J, et al. Extending the methodology of X-ray crystallography to allow imaging of micrometer-sized non-crystalline specimens[J]. Nature, 1999, 400: 342−344
2 Wei M, Attwood D T, Anderson E, et al. Patterning a 50 nm period grating using soft X-ray spatial frequency multiplication[J]. Journal of Vacuum Science & Technology B, 1994, 12(6): 3648−3654
3 Chubar O, Chu Y S, Kaznatcheev K, et al. Application of partially coherent wave front propagation calculations for design of coherence-preserving synchrotron radiation beamlines[J]. Nuclear Instruments and Methods in Physics Research, 2011, A649(1): 118−122
4 Coisson R, Marchesini S. Gauss-schell sources as models for synchrotron radiation[J]. Synchrotron Radiation, 1997, 4: 263−266
5 Singer A, Vartanyants I A. Modelling of partially coherent radiation based on the coherent mode decomposition[C]. Proceedings of SPIE Conference Advances in Computational Methods for X-ray Optics II. California, USA, 2011: 814106
6 王华, 闫帅, 闫芬, 等. 上海同步辐射装置波荡器光源空间相干性的研究[J]. 物理学报, 2012, 61(14): 144102-6
WANG Hua, YAN Shuai, YAN Fen, et al. Research on spatial coherence of undulator source in Shanghai Synchrotron Radiation Facility[J]. Acta Physica Sinica, 2012, 61(14): 144102-6
7 Chubar O, Elleaume P, Kuznetsov S. Physical optics computer code optimized for synchrotron radiation[C]. Proceeding of SPIE, Optical Design and Analysis Software II. Seattle, WA, 2002, 4769: 145−151
8 Samoylova L, Buzmakov A, Geloni G, et al. Cross-platform wave optics software for XFEL applications[C]. Proceeding of SPIE, Advances in Computational Methods for X-Ray Optics II. California, USA, 2011: 81410A
9 Bahrdt J. Wavefront tracking within the stationary phase approximation[J]. Physical Review Special Topics-Accelerators and Beams, 2007, 10(6): 060701−060714
10 孟祥雨, 郭春磊, 王勇, 等. 同步辐射光束线中部分相干光的传播研究[J]. 2013, 33(7): 0734001−1
MENG Xiangyu, GUO Chunlei, WANG Yong, et al. Research on partially coherent light propagation in synchrotron beamlines[J]. Acta Optica Sinica, 2013, 33(7): 0734001−1
11 Clarke J A. The science and technology of undulators and wigglers[M]. Oxford: Oxford University Press, 2009: 55−84
12 Onuki H, Elleaume P. Undulators, wigglers and their applications[M]. New York: Taylor & Francis Inc, 2003: 104−169
13 Geloni G, Saldin E, Schneidmiller E, et al. Fourier treatment of near-field synchrotron radiation theory[J]. Optics Communnications, 2007, 276(1): 167−179
14 Lauterborn W, Kurz T. Coherent optics: fundamentals and applications[M]. 2nd ed. New York: Springer, 1999: 46−75
15 Goodman J W. Statistical optics[M]. New York: John Wiley & Sons, 1985: 65−80
16 Geloni G, Saldin E, Schneidmiller E, et al. Transverse coherence properties of X-ray beamsin third-generation synchrotron radiation sources[J]. Nuclear Instruments and Methods in Physics Research, 2008, A588: 463−493
17 Paterson D, Allman B E, McMahon P J, et al. Spatial coherence measurement of X-ray undulator radiation[J]. Optics Communications, 2001, 195(1−4): 79−84
18 王云, 肖体乔, 徐洪杰, 等. 光学元件表面粗糙度对第三代同步辐射光源空间相干性的影响[J]. 光学学报, 2000, 20(4): 553−559
WANG Yun, XIAO Tiqiao, XU Hongjie, et al. Effect of surface roughness of optical elements on spatial coherence of X-ray beams from the third generation synchrotron radiation sources[J]. Acta Optica Sinica, 2000, 20(4): 553−559
CLCTL501.7
Investigation on the coherence of undulator source and soft X-ray interference lithography beamline in SSRF
GUO Chunlei MENG Xiangyu WU Yanqing WANG Yong TAI Renzhong
(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China)
Background:Synchrotron radiation (SR) has some unique features such as higher brightness and continuously adjustable wavelength. Sometimes SR source will be a unique choice in some experiments. And with the development of the SR facility, especially the appearance of various low emittance undulators, the experiments such as coherent diffraction imaging (CDI) that needs high brightness coherence source can be conducted. The traditional ray trace software, such as Shadow, using the geometrical optics methods, could not be applied for the coherent beamlines. Purpose: We want to provide a basis for the beamline design and the X-ray coherent experiments, the effective evaluation of the spatial coherence in beamlines is needed. Undulator source, which can be calculated precisely, will become a plane source with some features. As the source of the beamline, undulator was calculated. And the spatial coherence of the exit slit can be calculated too. So we can analyze the coherence of the beamline. Methods: Firstly, we used BPM to measure the intensity of the diffraction of the slit, and simulated the intensity distribution of the slit diffraction using the MCI (a software written by ourselves) to confirm the coherent length of the secondary source at slit. Secondly, we calculated the undulator supposed as a plane source, and used the MCI to numerically calculate the propagation of partially coherent X-ray in the soft X-ray interference lithography beamline from the undulator to the exit slit. Finally, we compared the difference of the coherent length at the slit by the above two methods. Results: We calculated the coherent length at the different place in the beamline, such as mirrors and slits. The most important thing was that we could not only know the coherent length with different size of the slits, but also control the spatial coherence quantitatively. When the slit size was 40 μm×40 μm, the spatial coherence was almost fully coherent. And we used the method to do some simulation about the coherent experiments and the coherent beamline design. Conclusions: The new method was available for the coherence analysis of the beamline. The calculation of the undulator was proper. And the quantitative analysis and control of spatial coherence could provide a basis for the X-ray coherent experiments and the coherent beamline design.
X-ray optics, Spatial coherence, Undulator, Coherent length
TL501.7
10.11889/j.0253-3219.2013.hjs.36.090101
国家自然科学基金项目(11005146和11275255)资助
郭春磊,男,1987年出生,2013年于中国科学院上海应用物理研究所获硕士学位,主要从事相干光束线设计及其相干性的研究
吴衍青,E-mail: wuyanqing@sinap.ac.cn;王勇,E-mail: wangyong@sinap.ac.cn
2013-03-14,
2013-05-16

