梯度与曲率变形力相结合的图像配准方法
——大形变非刚性图像配准
贾义亭,祝 轩,蔺恩标,雷文娟
西北大学 信息科学与技术学院,西安710127
1 引言
图像配准就是对在不同时间、不同传感器等不同条件(天候、照度、摄像位置和角度等)下获得的两幅或多幅图像根据某种配准测度函数,寻找一种空间变换关系,使经过空间变换后两幅图像间的相似性最大或者差异性最小。图像配准(Image registration)被广泛地应用于遥感数据分析、计算机视觉、医学图像分析和军事目标自动识别等领域,是图像处理领域的一个重要研究方向。图像配准方法通常分为两类:一类是刚性配准,另一类是非刚性配准。刚性配准适合于刚性物体形变的配准,其只能对图像进行全局线性变换,使它在图像配准方面存在很大的局限性,目前刚性配准技术已经发展得比较成熟。自然界中多数物体的形变都属于非刚性形变,非刚性配准[1]能够更精确地实现局部变形,其配准技术有待进一步提高,基于此图像的非刚性配准算法研究受到相关人员的高度关注。
非刚性配准方法主要分为两大类:基于像素的方法和基于特征的方法。其中基于像素的方法不需要对图像进行分割,可避免因分割带来的边缘效应和误差,是目前公认的较好的方法之一。Hellier 等人[2]对配准方法的比较研究表明Demons 配准算法对非刚性形变具有较高的配准精度。文献[3]则指出Demons 算法只适用于小形变配准,对大形变问题Demons 算法将不能保持图像的拓扑结构,并产生物理上的不合理形变。此外,Demons算法还存在仅靠梯度信息来确定浮动图像的位移量,当梯度非常小时,图像形变的方向不能被确定,往往会导致错误的配准变换[3]。针对Demons 算法的弊病,Wang 等人[4]提出了改进的Active Demons 算法,将牛顿作用力与反作用力原理引入Demons算法,假设扩散是双向的,认为不但可以用参考图像的梯度信息作为驱动力使浮动图像向参考图像扩散,同时施加反向作用力使参考图像向浮动图像扩散。Active Demons算法能够部分克服Demons 算法的缺陷,特别是在提高大形变配准的正确性和一致性方面具有一定优势。
Active Demons 配准算法[5]是一种将形变配准视作扩散问题的基于灰度的非刚性配准方法,其利用参考图像的灰度梯度信息作为驱动力实现浮动图像与参考图像的配准。
随着对图像局部特征研究的深入,人们认识到仅用一阶微分量——梯度来表征图像局部特征是不够的,二阶微分量中含有更丰富的信息。Sapiro 和Caselles 指出图像中物体的形状信息取决于等照度线(isophoto)的形态学特征[6-7]。在文献[3]中将图像等照度线的曲率作为一个校正形变的驱动力因素引入Demons 扩散方程,建立了一个基于梯度和曲率变形力相结合的扩散模型(简称G&C model),实现了小形变图像的精确配准。更进一步将等照度线的曲率引入Active Demons 算法,提出改进的Active G&C 模型,并在Active G&C 模型应用于大形变图像配准的算法实现过程中加入多分辨率策略,使梯度与曲率变形力相结合的Active G&C 配准模型不仅能够克服Active Demons算法仅依靠梯度信息易导致错误配准的弊病,而且在提高大形变图像的配准精度方面明显优于Active Demons 算法。本文通过实验对上述内容进行验证,结果表明提出的方法行之有效。
2 Active Demons算法
Demons 算 法 是Thirion 等 人[5]根 据 经 典 的Maxwell’s demons 热力学实验,提出的一种基于光流场的非刚性图像配准模型,其配准思想是将配准过程看作是浮动图像的像素向参考图像逐步扩散的过程,扩散强度由参考图像的梯度信息确定,扩散方程如下:

其中m、s分别表示浮动图像和参考图像,∇s表示参考图像的梯度。
文献[4]提出改进的Active Demons 算法,该算法根据牛顿作用力与反作用力的原理,假设扩散是双向的,不仅利用参考图像的灰度梯度信息∇s使浮动图像向参考图像扩散,而且利用浮动图像的灰度梯度信息∇m使参考图像向浮动图像扩散,定义如下基于浮动图像的灰度梯度信息驱动力um:

其中,“-”表示反作用力。
结合式(1)和(2),得Active Demons算法驱动力:

其中,前项促使浮动图像向参考图像移动,后项促使参考图像向浮动图像移动。
具体在算法实现过程中引入归一化参数α[4],用来自适应地调节每次迭代中的驱动力,以加快收敛速度,得式(4):

3 梯度与曲率变形力相结合的大形变非刚性图像配准方法
记灰度图像u(x,y),其梯度是一阶量,可表示为∇u=(ux,uy),其中ux=∂u/∂x,uy=∂u/∂y,梯度信息反映图像中像素灰度值的变化强弱。图像的等照度线定义为Xλu={[x,y],u(x,y)=λ},等照度线是指图像中光顺的曲线,反映图像中物体的形状。文献[6-7]指出图像中物体的形状信息取决于等照度线的形态学特征。鉴于真实图像中的等照度线足够光顺,相应地描述等照度线形态学特征的二阶微分量——曲率的变化应该较小,然而因为浮动图像存在形变,造成其中的等照度线发生畸变,使曲率发生显著变化。基于上述分析,认为Demons 和Active Demons 算法仅靠梯度信息决定配准驱动力是不够的,为了使畸变的等照度线也变得比较光顺,将等照度线曲率作为另一个驱动力因素引入Active Demons 方程,使浮动图像在梯度和曲率双重驱动作用力下形变,定义如下两个曲率驱动力uk(m)和uk(s):

其中,f(k(s))和f(k(m))分别是以参考图像的曲率k(s)和浮动图像的曲率k(m)为自变量的曲率驱动函数,其作用是保持图像的结构信息,使等照度线变的光滑,“-”表示反作用力。
结合式(5)和(6),并引入归一化参数α,得:

将该模型称为梯度和曲率变形力相结合的配准模型(简称Active G&C model)。
本文选取如下曲率驱动函数:

以参考图像的曲率ks计算为例,如式(9):
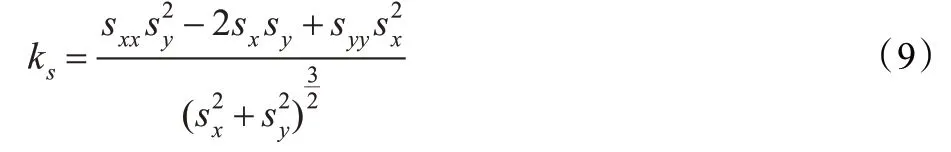
浮动图像的曲率km计算只需将式(9)中的s 换成m。
为了更进一步提高大形变图像的配准精度,在迭代求解Active G&C model 的过程中加入金字塔多分辨率策略,对浮动图像和参考图像进行多级金字塔分解,将低级金字塔图像计算得到的位移偏移量超采样后作为上一级金字塔图像的初始变换矩阵(如图1 所示),按照由粗到精逐级迭代的方式对配准结果优化。多分辨率策略不仅有利于提高配准算法的执行速度和精度,更重要的是可以避免配准过程中出现局部极值[8]。

图1 多分辨率策略示意图
Active G&C 算法实现过程如下:
步骤1设定初始偏移矩阵T0,设置金字塔级数K ,对浮动图像m 和参考图像s 进行K 级金字塔分解。
步骤2当前金字塔级数k <K 时,根据式(7)进行n 次迭代,得浮动图像m 相对参考图像s 的位移偏移矩阵更新偏移矩阵Tk=Tk-1+ukn。
步骤3用Tk使浮动图像形变,用均方误差MSE(式(10))作为形变后的浮动图像与参考图像的相似性测度,当相似性测度小于某设定阈值时,认为第k 级分辨率图像已收敛,进入第k+1 级,执行步骤4,否则继续迭代,计算ukn+1。

步骤4对前一级图像的偏移矩阵Tk-1超采样,作为当前图像配准的初始位移偏移量 执行步骤2。
步骤5K 级金字塔迭代完成后,将最终的位移偏移矩阵作用于浮动图像,得到最终的配准结果。
4 实验结果及评价
4.1 实验结果
在Matlab7.6 环境下,分别用Demons、Active Demons和本文方法分别对大形变Woman 图像进行配准。实验结果如图2 所示。实验迭代次数为200 次,进行三级金字塔分解,Active Demons和本文Active G&C 算法中α 取2.5。
一般情况下金字塔级数越高,配准效果越好,但是配准时间越长。可根据所处理对象的不同,权衡配准精度和时间效率之间的利弊加以选择。
观察图2可以看出本文方法在配准大形变图像时具有更好的视觉效果(如眼睛和嘴的部位),明显优于其他两种方法。
4.2 结果评价
为了进一步客观评价上述三种配准方法的配准质量,以大形变Elaine 图为例,采用不同的配准方法得图3 所示配准结果。通过在Elaine 图中的相同位置划线,绘制相应的灰度偏移曲线,比较不同配准方法配准大形变Elaine 图像后与参考图像之间的灰度偏移量,得图4(a)和(b),其中特别给出了本文方法和Active Demons 方法的灰度偏移比较曲线,如图4(b)。
观察对比图4 中灰度偏移曲线可知,采用多分辨策略的Active G&C 方法在处理大形变图像配准问题时优越性明显,配准结果中的各个像素点的灰度值与参考图像基本一致,可实现图像局部的精确配准,视觉效果更好。
分别用均方误差、峰值信噪比、相关系数、归一化互信息和结构相似度[9]五种客观评价方法比较Demons、Active Demons 和Active G&C 方法配准Elaine 图像的配准质量,得表1。

图2 Woman 图像配准

图3 Elaine图像配准
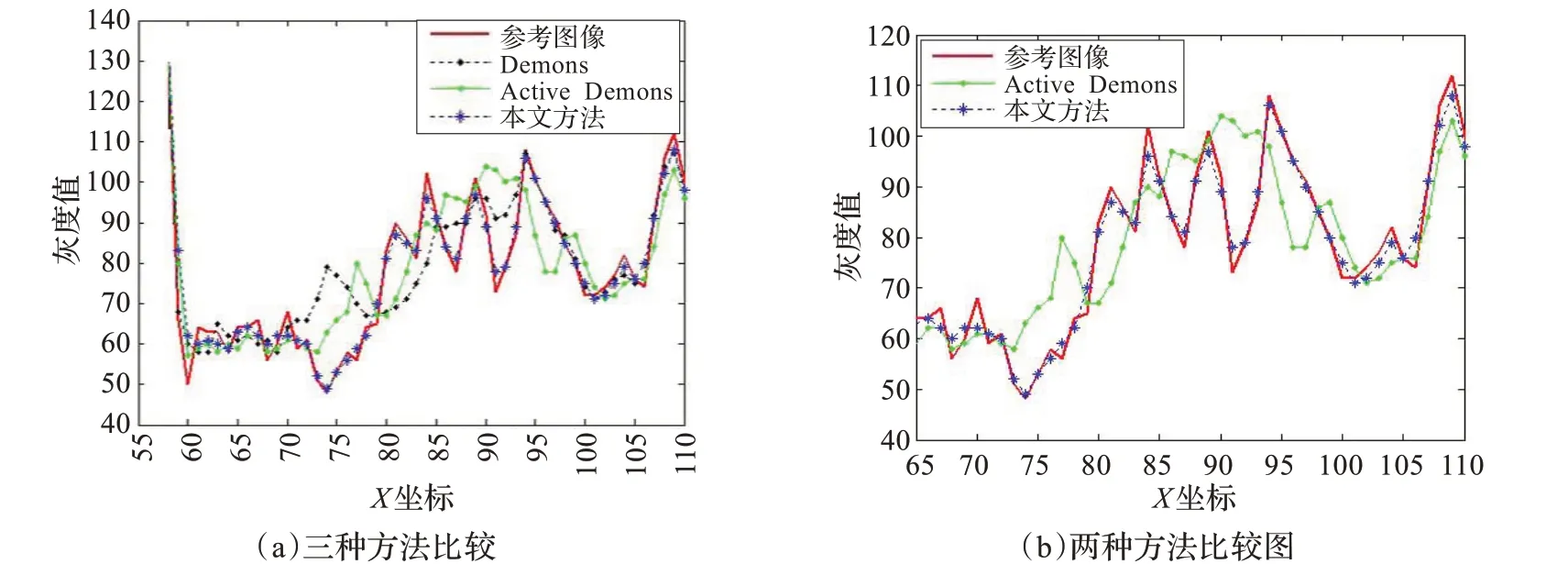
图4 灰度偏移比较

表1 质量评价比较
相关系数可以反映两幅图像之间的相似度,按式(11)计算:
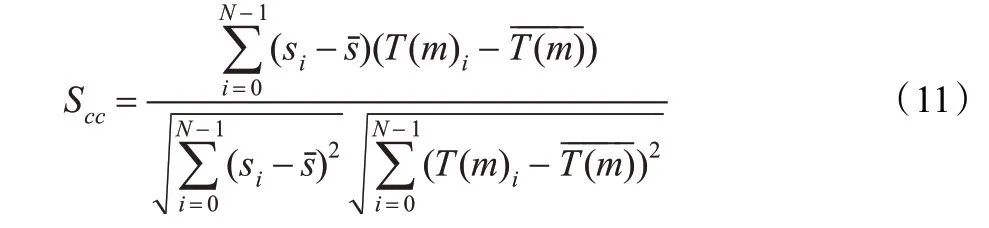
Scc越大配准效果越好。
结构相似度(SSIM)按式(12)计算:

其中,s为参考图像,T(m)为配准结果,S(s,T(m))是参考图像s与配准结果T( )m之间的结构相似度度量函数,α>0,β>0,γ>0,用来调整图像亮度、对比度和结构信息所占的比重,l(·),c(·),s(·)分别是浮动图像和参考图像之间亮度、对比度和结构的比较函数。
从表1 中可以看出,Active G&C 方法相比其他两种配准方法优势更明显。
5 结束语
本文将等照度线曲率引入Active Demons 算法,同时在算法迭代过程中采用金字塔多分辨率策略,建立了一个具有曲率和梯度双重驱动力相结合的配准扩散模型,该模型克服了仅靠梯度信息易导致错误图像配准以及对大形变图像配准精度不高的弊病。实验表明,本文方法是一种行之有效的图像配准算法。
[1] Crum W R,Hartkens T.Non-rigid image registration:theory and practice[J].British Journal of Radiology,2004,77:140-153.
[2] Hellier P,Barillot C,Corouge I,et al.Retrospective evaluation of inter-subject brain registration[J].IEEE Transactions on Medical Imaging,2003,22(9):1120-1130.
[3] 雷文娟.非刚性图像配准方法研究[D].西安:西北大学信息科学与技术学院,2008.
[4] Wang He,Dong Lei.Validation of an accelerated“demons”algorithm for deformable image registration in radiation therapy[J].Physics in Medicine Biology,2005,50(12):2887-2905.
[5] Thirion J P.Image matching as a diffusion process:an analogy with Maxwell’s demons[J].Medical Image Analysis,1998,2(3):243-260.
[6] Caselles V.Shape preserving local contrast enhancement[C]//Proceedings of the 1997 International Conference on Image Processing(ICIP’97).Washington:IEEE Computer Society,1997:314-317.
[7] Sapiro G,Caselles V.Histogram modification via differential equations[J].Journal of Differential Equations,1997,135(2):238-268.
[8] 张红颖,张加万,孙济洲.改进Demons 算法的非刚性医学图像配准[J].光学精密工程,2007,15(1):145-150.
[9] Wang Zhou,Bovik A C.Modern image quality assessment(synthesis lectures on image,video & multimedia processing)[M].[S.l.]:Morgan & Claypool Publishers,2006.

