变刚度双稳态电磁式振动发电机的AMESim仿真分析
朱 沛,梁义维,赵利平
(太原理工大学,山西太原030024)
0 引 言
振动式发电机可以把振动能转换成电能,为无线产品和MEMS器件供电。并且电磁式振动能量采集器最具有体积小、感测频率高、发电量大、工艺与半导体技术兼容、无需驱动电源、可应用于各种恶劣环境等优点。但传统的线性机构只能收集其固有频率附近的振动能,响应频带窄[1]。为了拓宽频带,国内外研究者尝试了不同的方案:重庆大学于慧慧等人采用多悬臂梁-单质量块结构[2];国防科技大学陈仲生等人[3]、意大利Brescia大学的M.Ferrari[4-5]等人均采用在悬臂梁自由端放置永磁铁,构建一种双稳态拾振机构;土耳其中东科技大学的Ibrahim Sari等人采用多悬臂梁阵列结构[6];上海交通大学的马华安等人设计了在悬臂梁上放置永磁铁,并在梁的上下方放置永磁铁这样一种结构[7]。以上这些结构都起到了拓宽响应频带的作用,其中双稳态结构的应用是当前研究的新方向。但以上结构在弱信号小振幅激励下,无法形成双稳态的情况,本文采用变刚度弹性机构,发电机在小振幅激励下,提高响应振幅,形成双稳态,从而拓宽响应频带,提高发电功率。
1 双稳态振动发电工作原理
双稳态电磁式振动发电机指采用双稳态拾振机构,从周围环境中吸收振动能,把环境振动能转换为拾振机构的机械能,拾振机构性能的优劣直接影响振动能量收集效率,再通过磁电转换系统,把机械能转换成电能。
1.1 发电原理
电磁转换系统实现机械能向电能的转换,利用永磁体布置磁场回路。其原理是根据法拉第电磁感应原理,磁通量的变化产生感应电动势。其中,E表示感应电动势,Φ表示通过线圈的磁通量,N表示线圈匝数,B表示磁感应强度,S表示线圈面积矢量。由公式知道,线圈中的磁通量的变化是产生电压的原因,而引起磁通量Φ变化有两种原因,一种是线圈完全处于磁场中,面积S不变,磁感应强度B变化,由此产生的电动势叫做感生电动势,另一种是线圈部分处于磁场中,随着线圈的运动,面积S变化,此种方式产生的电动势叫做动生电动势[8-9]。本文结构设计采用动圈式,产生的是动生电动势。
1.2 双稳态现象的产生
双稳态是指在其运动过程中有两个稳定平衡状态,在其从一个稳定平衡状态运动到另一个稳定平衡状态的过程中,机构需要克服势垒做功。处于两个稳定平衡状态时,机构不需要外力/力矩来维持即可稳定在既定位置。双稳态机构振动过程中产生从一个平衡位置到另一个平衡位置的现象,称为势阱逃逸现象,这种现象伴随着大振幅跳跃[10],把势阱逃逸现象运用到拾振机构的设计,以改进传统弹簧振子拾振机构效率低的缺点。
2 建模仿真
2.1 系统建模
为了使弹性梁具有双稳态,本文采用外加磁场的方法,合理布置永磁铁,在弹性梁自由端形成磁场,提供非线性回复力。结构示意图如图1所示。

图1 双稳态结构示意图
发电机的整体仿真模型如图2所示,由拾振机构和电磁转换系统两部分组成。拾振机构由弹簧质量振子、外部磁场构成,外部磁场提供非线性回复力,使得振子具有双稳态行为。磁场的布置采用永磁体模块和磁性单元模块。
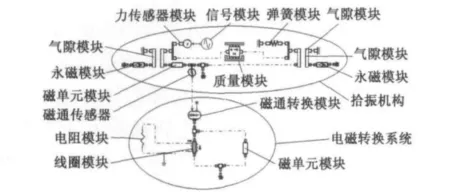
图2 整体模型
模型中,采用弹簧质量模块模拟弹性梁,永磁铁模块和磁性单元模块模拟永磁铁磁场,信号源模块模拟振动信号。通过磁通传感器把变化的磁通量输入线圈,磁通传感器测试磁场中不同位置的磁感应强度。电磁转换系统由电阻模块、线圈模块、磁通转换模块、磁单元模块组成,磁通转换模块接收磁通传感器输出的磁通变化率信号,并转化为磁通信号输出给线圈,采用电阻模块作为外接负载和线圈模块形成电路回路,根据法拉第电磁感应原理实现磁电的转换。该模型是通过引入非线性的磁场力和变刚度弹簧弹力共同作用形成双稳态结构。
2.2 仿真分析
模型中各个模块的参数设置,如表1所示。

表1 参数设置
变刚度弹性机构刚度k值与响应幅值a1的设置,如表2所示。

表2 k值设置
根据胡克定律F=ks,刚度k与位移s成反比,通过减小弹性机构刚度,增大响应振幅。对应的弹性机构力-位移关系如图3所示。

图3 力-位移图
幅值a1和刚度k成正比,随着a1的减小,对应k值减小,根据公式F=ks,在环境激励F一定时,弹簧刚度越小,响应振幅越大。提高拾振机构在微弱振动下的振幅,使拾振机构达到双稳态,提高发电机在小振幅振动时的发电功率。
输入一系列不同频率(f=5~200 Hz,a=0.3)的正弦周期信号,模拟环境振动,对比变刚度双稳态系统、单一刚度双稳态系统和不引入磁场力的线性系统在不同频率下对应的发电功率。描点拟合,结果如图4所示。
由图4可知,线性系统的响应频率集中在140 Hz附近,单一刚度双稳态电磁式发电机拓宽了响应频率,在80~130 Hz频率范围内,发电功率达到0.2 mW以上。变刚度系统对频宽的拓展更大,发电功率在0.2 mW以上的频率范围是5~180 Hz。
分别取输入信号 a=0.1、a=0.2,频率取 f=5~200 Hz,对比变刚度系统在小振幅环境激励下的功率特性,如图5、图6所示。
由图5、图6可知,变刚度系统提高了在小振幅激励下的发电功率,拓宽了响应频带。

改变输入信号幅值,a 依次取 0.02、0.05、0.08、0.1、0.2、0.3、0.5、0.7,频率 f=5 ~200 Hz,以频率、幅值以及对应的发电功率,分别绘制单一刚度和变刚度系统功率曲面图,如图7、图8所示。

由图7、图8可知,采用变刚度结构,拓展了频宽,功率峰值不再仅仅集中在单一频率附近,提高了在低频(f<100 Hz)、小振幅(a<0.3)激励下的功率。
3 结 语
本文基于AMESim仿真平台,建立了变刚度双稳态电磁式振动发电机模型,通过仿真分析,采用变刚度双稳态拾振结构拓宽了响应频带,频带宽度5~180 Hz,提高了对环境中振动能量的收集效率,提高了小振幅激励下的发电功率。将变刚度结构应用于宽频振动发电机的设计,对提高能量收集效率和发电功率是一种有效途径。
[1] 刘雪华.基于MEMS微型振动式发电机系统的研究[D].重庆大学,2006.
[2] 于慧慧,温志渝,温中泉,等.宽频带微型压电式振动发电机的设计[J].传感技术学报,2010,23(5):643-646.
[3] 陈仲生,杨拥民.悬臂梁压电振子宽带低频振动能量俘获的随即共振机理研究[J].物理学报,2011(07):437-443.
[4] Ferrari M,Bau M,Guizzetti M,et al.A single-magnet nonlinear piezoelectric converter for enhanced energy harvesting from random vibrations[J].Sensors and Actuators A,2011,172:287-292.
[5] Ferrari M,Ferrari V,Guizzettia M,et al.Improved energy harvesting from wideband vibrations by nonlinearpiezoelectric converters[J].Sensors and Actuators A,2010,162:425-431.
[6] Sari I,Balkan T,Kulah H.An electromagnetic micro power generator for wideband environmental vibrations[J].Sensors and Actuators A,2008,145-146:405-413.
[7] 马华安,刘景,全唐钢,等.一种宽频的磁式压电振动能量采集器[J].传感器与微系统,2011,30(4):66-68.
[8] 贾起民.电磁学[M].第2版.北京:高等教育出版社,2001.
[9] 邹继斌.磁路与磁场[M].哈尔滨:哈尔滨工业大学出版社,1998.
[10] 陈予恕.非线性振动[M].第2版.天津:天津科学技术出版社,1983.

