220 kV支持式管型母线结构抗震性能
谢韬,孙启林,林康立,袁广林,张锐,舒前进
(1.江苏省电力公司徐州供电公司,江苏省徐州市221005;2.中国矿业大学力学与建筑工程学院,江苏省徐州市221008;3.国网北京经济技术研究院徐州勘测设计中心,江苏省徐州市221005)
0 引言
电力系统作为我国生命线工程的重要组成部分,在地震中一旦失效或遭到破坏,将严重影响正常的生产、生活和抗震救灾工作,并且可能导致严重的次生灾害[1-3]。输变电系统中的管型母线结构,由多个∏式支架、支柱绝缘子和管型母线组成,其体型高大,支架之间相互影响,地震时的反应比较复杂。文献[4-6]对管型母线连接系统的地震响应进行了数值理论分析,认为地震中管型母线结构是输变电体系中极易破坏的部分。文献[7]在收集汶川地震震害资料的基础上,利用ABAQUS软件分析了支持式管型母线的动力特征,认为支持式管型母线的最大受力出现在支柱绝缘子的根部,但是没有对结构在各烈度条件下的安全性做出评价。
本文以220 kV支持式管型母线结构为研究对象,通过ANSYS软件建立模型,采用时程分析方法,研究管型母线结构在地震作用下的动力响应特点,分析结构在不同地震烈度下的抗震性能,并对结构的安全性做评价。
1 有限元模型
220 kV变电站中常用的支持式管型母线结构由7组支持装置和3相管型母线组成,共6跨,每跨跨距13 m。支持装置的下部为∏式支架,高约7 m,支架上安装3组绝缘子支柱,每组绝缘子高约2.4 m,绝缘子伞径265 mm,胶装部位直径170 mm,胶装深度110 mm。每组顶部分别连接一相根管型母线,管型母线内径0.24 m,外径0.26 m。
1.1 单元的选取
∏式支架和支柱绝缘子形状细长,地震时会出现弯曲变形,因此采用Beam188梁单元来模拟。Beam188梁单元是基于铁木辛哥(Timoshenko)梁结构理论的三维线性(2节点)或者二次梁单元,适用于细长-中等短粗的梁结构,同时能够考虑剪切变形的影响。管型母线与部分支柱绝缘子通过温度节连接,温度节具有一定变形能力,使两者之间可以发生一定的相对位移,因此用Combin14单元模拟温度节连接,根据文献[8]的试验数据,单元的弹性设为100 N/mm。Combin14单元是弹簧-阻尼单元,具有1、2维或3维的轴向或扭转的性能。每个节点具有3个自由度。
1.2 材料常数的确定
模型中支柱绝缘子为陶瓷材料,瓷质材料为脆性材料,计算中忽略其塑性变形,只考虑线弹性变形。∏式支架为钢材,管型母线为铝管,如果地震作用较大,金属材料会出现塑性变形,因此使用双线性各向同性模型,定义2种材料的弹塑性本构关系。各材料属性见表1。
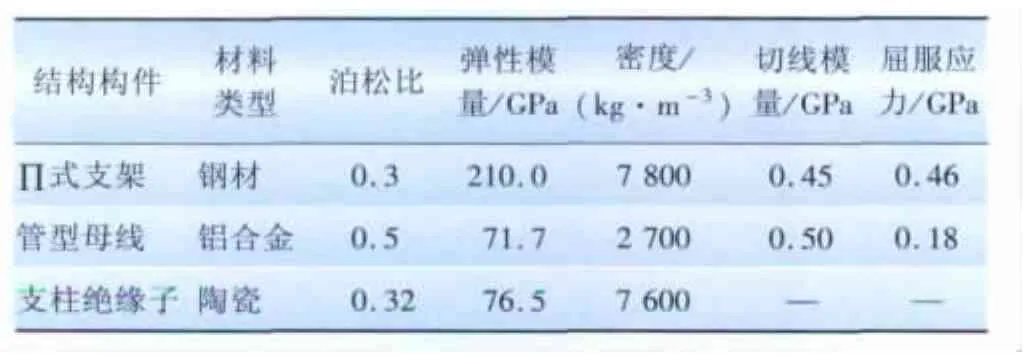
表1 支持式管型母线结构材料参数Tab.1 Material parameters of supported tubular bus
1.3 模型的约束条件及连接
∏式支架的基础简化为固定端支座。∏型钢支架和绝缘子之间通过6组螺栓相连接,因此可以将其视为刚性连接,采用等效实心梁模拟,通过调整梁的截面使其刚度与实际设备一致,调整梁的密度,使其质量与实际设备相等。每组绝缘子上下瓷瓶之间通过8组螺栓连接,同样视为刚接。在支持式管型母线结构中,管型母线与支柱绝缘子的连接方式分为:(1)固定式金具连接,如图1(a)所示,母线和金具之间紧固连接无任何滑动,连接节点设定为固结;(2)滑动式金具连接,母线可以在沿着结构的长度方向上的水平滑动,如图1(b)所示,连接节点只约束连接处竖直方向和垂直于结构长度方向的位移以及转动;(3)温度节连接,两者之间具有部分滑动能力,如图1(c)所示,连接节点设置为弹簧—阻尼单元,该单元两端在结构长度方向上的水平位移不一致,但是不产生竖向位移和垂直于结构长度方向位移。

图1 绝缘子与管型母线连接方式Fig.1 Connection mode between tubular bus and insulator
1.4 网格的划分
支持式管型母线结构体型高大,必须合理确定网格的大小,才能既保证计算的精度,又不至于使单元数目太大,计算困难。为此,采用控制单元网格边长的方法,使结构单元划分比较均匀。有限元计算模型网格划分如图2所示。每个模型的节点数约为18 500个,单元数约为9 000个。
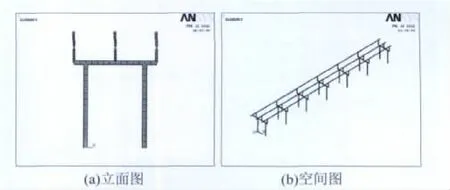
图2 支持式管型母线模型Fig.2 Model of supported tubular bus
2 模态分析方法与结果
模态分析的内容主要包括固有频率的计算和相应振型的确定。固有频率与被测结构的刚度、质量以及外形尺寸有关。结构外形不变时,其刚度越大则结构的固有频率越高,质量越大,固有频率越低。振型是体系的一种固有的特性,与固有频率相对应,即为对应固有频率体系自身振动的形态,反映了结构在共振时的可能破坏形式。
根据IEEE Std 693规范推荐的取值范围,结合工程实际,结构的阻尼比采用0.03。使用ANSYS软件的子空间法,计算得到前10阶自振频率为:1.073 7、1.136 0、1.391 1、1.630 2、1.994 2、2.095 6、2.117 9、2.139 3、2.296 5、2.478 9 Hz。其前4阶振型如图3所示。第1阶振型为端部支架发生弯曲变形,管型母线从中滑落;第2阶振型为结构整体发生弯曲变形,管型母线从一端滑落;第3阶振型为端部支架发生弯曲变形,但管型母线仍然与其连接;第4阶振型为端部支架发生扭曲变形。
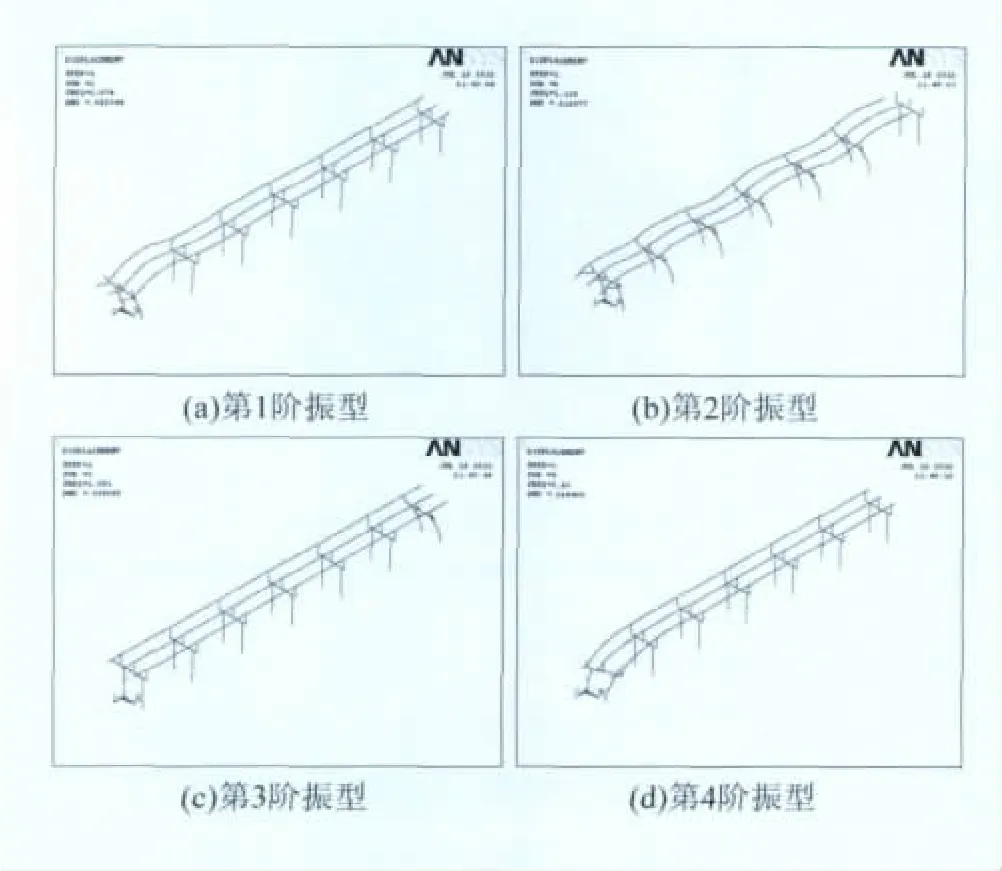
图3 支持式管型母线结构的前4阶振型Fig.3 First four vibration modes of supported tubular bus structure
3 时程分析
3.1 地震波的选取
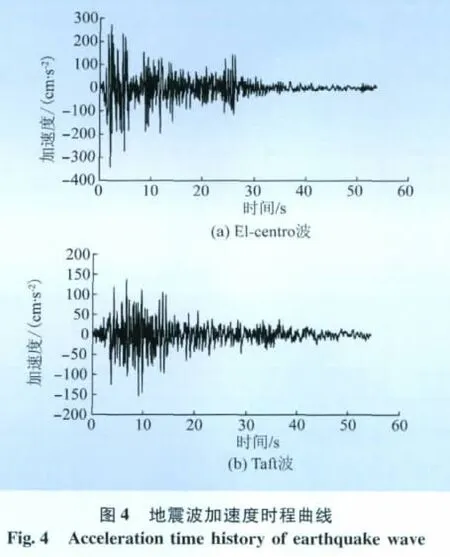
本文所用地震时程数据为 El-centro波和Taft波,加速度时程如图4所示。El-centro波是1940年5月18日美国加州Imperial Valley地震记录的加速度时程,持续时间为53.73 s,适合Ⅱ类场地土。Taft波是1952年7月21日美国California地震记录的加速度时程,持续时间为54.38 s,适合Ⅲ类场地土。为了研究不同地震烈度下支持式管型母线结构的抗震性能,根据GB 50011—2010《建筑抗震设计规范》对抗震设防烈度的要求,设计3种地震烈度条件,分别为:7度罕遇地震(基本设防烈度0.1 g,g为重力加速度),最大加速度2.2 m/s2;8度罕遇地震(基本设防烈度0.3 g),最大加速度5.1 m/s2;9度罕遇地震,最大加速度6.2 m/s2。同时,设定地震荷载作用的方向为沿着结构方向(以下简称顺向)和垂直于结构方向(以下简称法向),如图5所示。

3.2 加速度时程数据分析
计算结果表明结构的最大加速度出现在支柱绝缘子的顶部,并且绝缘子的位置不同,以及与管型母线连接方式不同都会影响加速度峰值。将计算到的各烈度下支柱绝缘子最大加速度如表2所示。
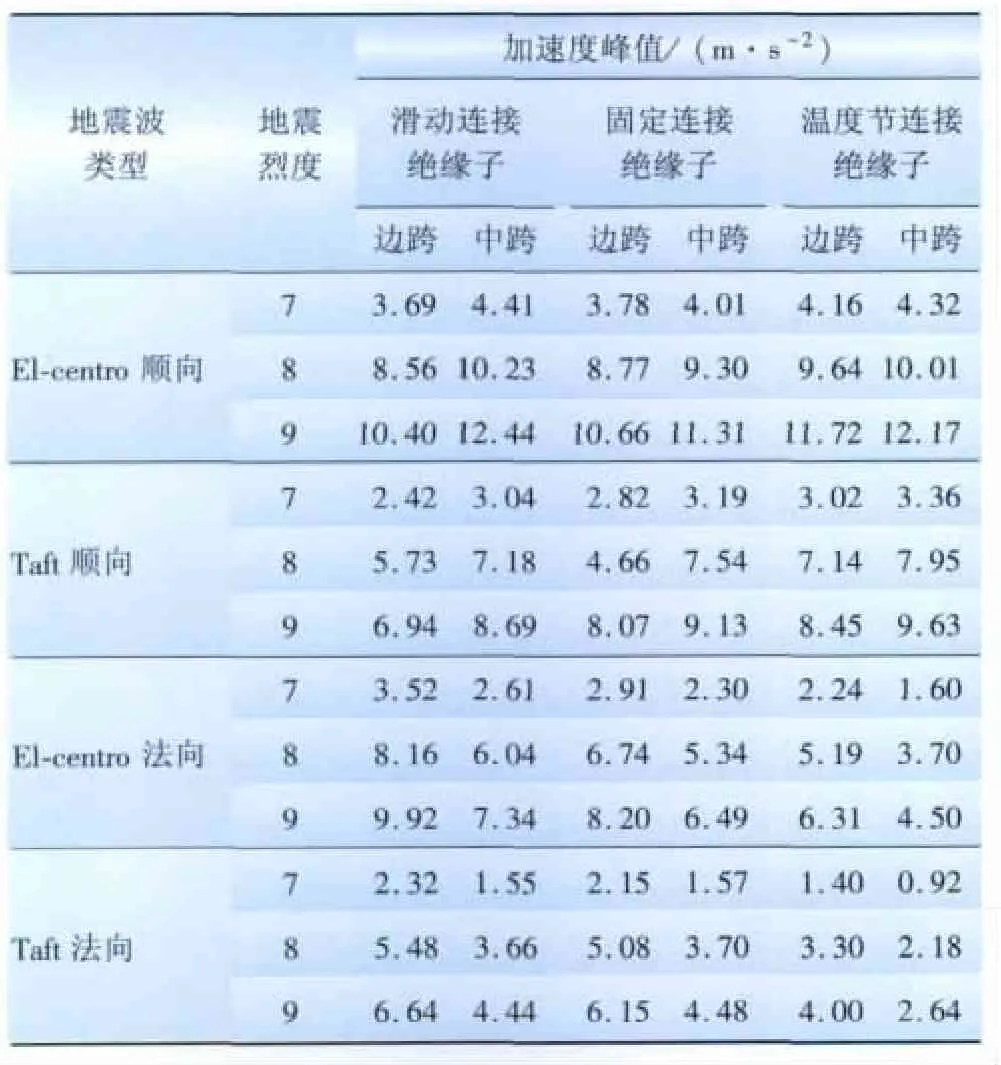
表2 各地震烈度下支柱绝缘子的加速度峰值Tab.2 Peak acceleration of insulators under different seismic intensity
由表2可知:
(1)在同等地震烈度下,顺向施加El-centro地震波时,支柱绝缘子的加速度峰值为施加Taft地震波时的1.2~1.5倍。法向施加El-centro地震波时,支柱绝缘子的加速度峰值为施加Taft地震波时的1.3~1.7倍。
(2)顺向施加El-centro地震波,结构的加速度峰值为法向施加El-centro地震波时的1.3~2.7倍。顺向施加Taft地震波,结构的加速度峰值为法向施加Taft地震波时的1.3~1.7倍。
(3)在相同地震荷载同等烈度作用下,顺向加载时中跨的支柱绝缘子加速度峰值约为边跨支柱绝缘子加速度峰值的1.2~1.3倍。在相同地震荷载同等烈度作用下,法向加载时中跨的支柱绝缘子加速度峰值约为边跨支柱绝缘子加速度峰值的70%~80%。
(4)顺向加载时,与管型母线固定连接的支柱绝缘子的加速度峰值约为温度节连接的支柱绝缘子加速度峰值的80%~90%。
为了进一步分析结构在不同加载条件下的动力响应特征,以及∏式支架对地震作用的放大效果,定义动力放大系数

式中:amax、ainput分别为结构的加速度峰值和地震波最大输入加速度。
计算7度地震下,不同位置支柱绝缘子的动力放大系数,计算结果如图6所示,图中A表示边跨位置的管型母线滑动连接支柱绝缘子,B表示中跨位置的管型母线滑动连接支柱绝缘子,C表示边跨位置的管型母线固定连接支柱绝缘子,D表示中跨位置的固定滑动连接支柱绝缘子,E表示边跨位置的管型母线温度节连接支柱绝缘子,F表示中跨位置的管型母线温度节连接支柱绝缘子,位置如图5所示。

图6 支柱绝缘子加速度放大系数Fig.6 Acceleration amplification factor of insulators
由图6可知:在El-centro地震波的作用下,各支柱绝缘子的加速度峰值非常大,在地震波顺向加载条件下,各支柱绝缘子的极限加速度是输入地震波的1.5~2倍,而在地震波法向加载时,前者是后者的1~1.5倍;在Taft地震波作用下,各支柱绝缘子的加速度峰值差距比较大,在法向作用下,除边跨上与管型母线滑动连接的绝缘子外,其余支柱绝缘子的加速度均小于输入地震波。
3.3 应力数据分析
计算结果表明,支柱绝缘子的最大弯矩出现在底部与∏式支架连接处,不同加载条件下各支柱绝缘子极限弯矩如表3、4所示。

表3 顺向地震荷载作用下的支柱绝缘子极限弯矩值Tab.3 The maximum bending moment of insulators in forward seismic load
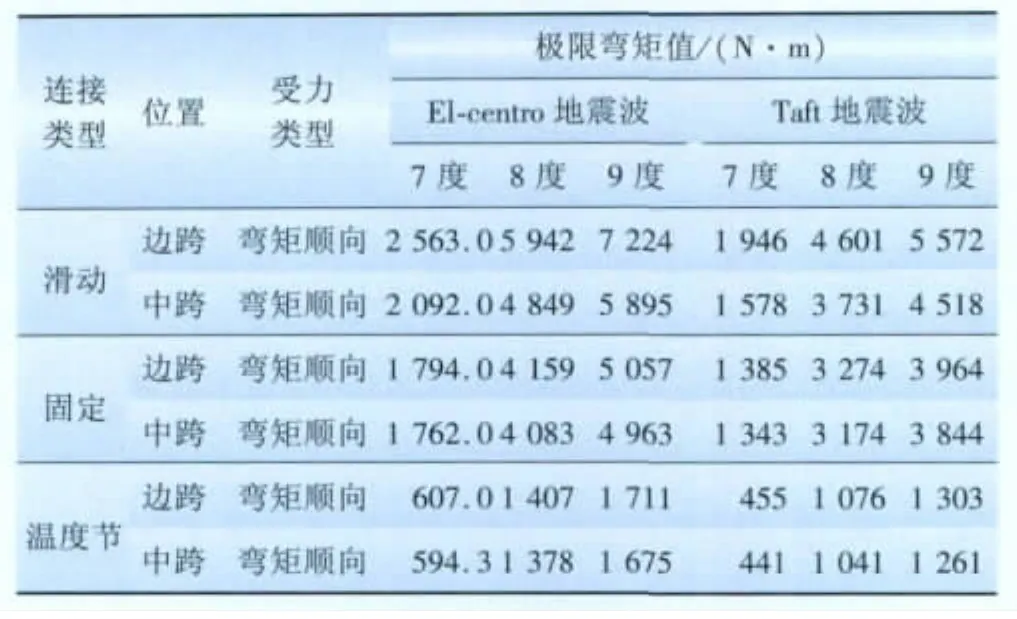
表4 法向地震荷载作用下的支柱绝缘子极限弯矩值Tab.4 The maximum bending moment of insulators in normal seismic load
对比表3、4中数据,可以发现以下规律:
(1)当地震烈度相同时,El-centro地震波作用下支柱绝缘子产生的极限弯矩大于Taft地震波。
(2)当地震荷载沿法向作用在结构上时,支柱绝缘子处于单向受弯状态,边跨的支柱绝缘子极限弯矩总是大于中跨支柱绝缘子。
(3)当地震荷载沿顺向作用在结构上时,支柱绝缘子的受力分为3种情况。①边跨上与管型母线固定连接的支柱绝缘子受到顺向弯曲和扭转的组合作用;②边跨上与管型母线通过温度节连接的支柱绝缘子在顺向和法向这2个相互垂直的方向上受到弯曲作用;③其余支柱绝缘子处于单向受弯状态。
(4)当烈度9度的地震荷载沿顺向作用在结构上时,与管型母线固定连接的支柱绝缘子的极限弯矩超过9 kN·m,而与管型母线滑动连接的支柱绝缘子的极限弯矩约为2 kN·m,与管型母线温度节连接的支柱绝缘子的极限弯矩约为0.1 kN·m。
因为支柱绝缘子所用的陶瓷为脆性材料,其抗拉强度远远低于抗压强度,可以使用第一强度准则判断其是否破坏。该强度理论认为当作用在构件上的外力过大时,其危险点处的材料就会沿最大拉应力所在截面发生脆断破坏,也就是认为不论在什么样的应力状态下,只要构件内一点处的3个主应力中最大的拉应力σ1达到材料的极限值,构件就会破坏。分别计算各绝缘子支柱的主应力值。
(1)单向受弯构件的主应力计算公式为

式中:M为弯矩;W为抗弯截面系数,对于等截面圆筒型构件,其表达式为
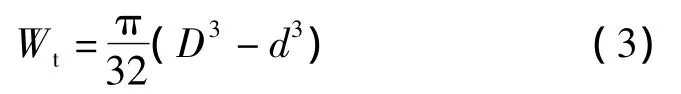
式中:D为外圆直径;d为内圆直径[9]。
(2)双向受弯构件的主应力计算公式为
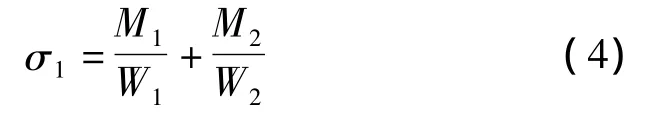
式中:M1和M2分别为顺向、法向2个方向上的弯矩;W1和W2分别为顺向、法向2个方向上的抗弯截面系数[9]。
(3)弯扭组合状态下主应力值计算。构件受到弯扭组合作用时,其主应力计算公式为
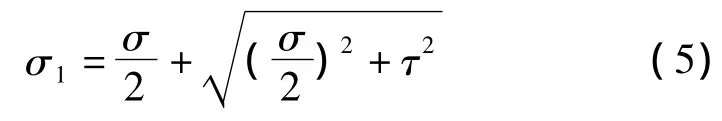
式中:σ为弯矩应力;τ为扭转产生的剪力,其表达式为

式中:T为扭矩;Wt表示截面抗扭系数,对于等截面圆筒型构件,其表达式[9]为

各支柱绝缘子最大拉应力计算结果如表5所示。
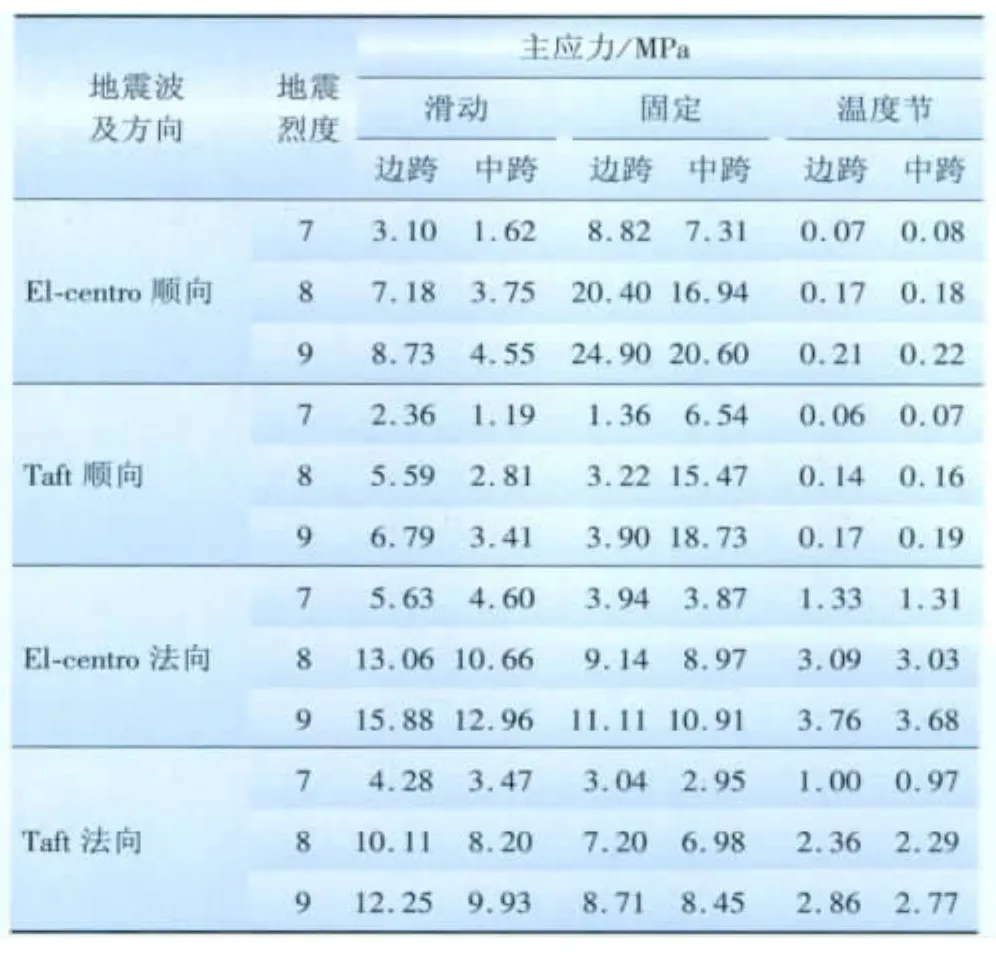
表5 支柱绝缘子主应力Tab.5 Main stress of insulators
GB 50260—96《电力设施抗震设计规范》规定:在进行变电站电气设备抗震设计时,支柱绝缘子的许用应力取值为12 MPa[10-11]。将表5中数据与支柱绝缘子的许用应力取值进行比较,可以得出以下结论:
(1)在7度地震烈度作用下,无论使用哪种地震波数据,以及加载方向如何,支柱绝缘子的极限应力均未超过许用应力,如果不考虑其他荷载(如风载)的组合作用,结构处于安全状态。
(2)在8度及以上地震烈度作用下,当施加荷载为El-centro地震波时,无论施加方向如何,都会有支柱绝缘子的受力超出许用应力,结构处于危险状态。
(3)在8度地震烈度作用下,当施加荷载为Taft地震波顺向时,中跨与管型母线固结的支柱绝缘子受力超出许用应力,结构处于危险状态[10]。
4 结论
(1)220 kV支持式管型母线结构的前10阶自振频率为1~3 Hz,处于地震波的卓越周期内,地震时结构容易出现共振。
(2)在不同地震荷载作用下,支柱绝缘子的最大弯矩都出现在底部,断裂破坏也最可能出现在这一部位,这与震害调查结果相一致。
(3)根据有限元时程计算和主应力计算结果,当地震荷载的烈度为7度及以下时,支柱绝缘子的最大拉应力小于陶瓷材料的设计极限应力,在地震中,如果不同时作用其他荷载(如风载),可以认为结构处于安全状态。
(4)在烈度为8度及以上的地震荷载作用下,会有部分位置的支柱绝缘子因受力超出材料的极限应力而发生断裂,结构处于危险状态。因此在抗震设防烈度为8度地区内建设变电站,需要对支持式管型母线结构进行加强,或者选用其他形式的母线结构。
[1]文波,牛荻涛,赵鹏.变电站抗震性能研究综述[J].工程抗震与加固改造,2007,29(6):73-77.
[2]张子引,袁兆祥,胡明.输变电工程抗震设计研究报告[R].北京:国网北京经济技术研究院,2009.
[3]贺海磊,郭剑波,谢强.电气设备的地震灾害易损性分析[J].电网技术,2011,35(4):25-28.
[4]Song J H,Kiureghian A D.Seismic response and reliability of electrical substation equipment and system[R].PEER,2005.
[5]Stearns C,Filiatrault A.Electrical substation equipment Interaction:experimental rigid conductor studies[R].PEER,2004
[6]Dastous J B,Kiureghian A D.Application guide for the design of flexible and rigid bus connections between substation equipment subjected to earthquakes[R].PEER,2010.
[7]谢强,朱瑞元.汶川地震中支持式管型母线破坏机理分析[J].电力建设,2010,31(3):8-12.
[8]Song J H,Kiureghian A D.Generalized bouc-wen model for highly asymmetric hysteresis[J].Journal of Engineering Mechanics,2006,132(6):610-618.
[9]刘洪文.材料力学[M].5版.北京:高等教育出版社,2011:356-365.
[10]GB 50260—96电力设施抗震设计规范[S].北京:中国电力出版社,1996.
[11]张伯艳,方诗圣,范知好.高压电气设备的抗震计算[J].中国电力,2001,34(1):44-47.

