基于谐波小波的自适应谱线增强及其应用研究

赵景波，刘慧敏，张磊

(青岛理工大学 自动化工程学院,山东青岛 266520)

基于谐波小波的自适应谱线增强及其应用研究

赵景波，刘慧敏，张磊

(青岛理工大学 自动化工程学院,山东青岛 266520)

针对随着传播距离的增大极低频电场衰减很快，很容易被环境噪声所掩盖，提出了基于谐波小波的自适应谱线增强器来提高微弱轴频电场远程检测能力的算法。根据实际情况和仿真信号的特点，谐波小波对信号进行9层分解。利用该算法对舰船电磁场缩比模型产生的轴频电场的实测数据进行处理，结果表明该算法能够实时有效地将微弱的轴频电场特征信号从环境背景噪声中分离出来，大大提高了舰船轴频电场的检测能力。同时采用基于基于谐波小波算法的自适应谱线增强的自适应迭代次数比采用最小均方算法的自适应迭代次数少，说明采用基于谐波小波算法的自适应谱线增强能快速收敛。

轴频电场;小波;谐波小波;自适应;谱线增强

0 引 言

由于海水的导电性,舰船轴频电场随着传播距离的增大衰减很快,容易被环境噪声所覆盖,从而不容易被检测到。因此,为了增强舰船轴频电场的远程测量能力，人们在电路上想尽办法来降低其自噪声以提高信噪比,从而达到检测微弱电场信号的目的。如果通过改善测量电路还不能达到目的,则可以通过数字信号处理的方法来提高微弱信号的检测能力。

毛伟，林春生，周萌等人提出基于高阶FS谱对角切片的舰船轴频电场微弱信号检测方法,该方法能简单有效地将微弱轴频电场信号从低信噪比的数据中分离出来,但是处理的信号信噪比很难降到很低的水平[1-2]。刘彦琼,岳瑞永,天作喜,韩晶等人提出基于谐波簇自适应线谱增强器的舰船轴频电场检测方法,该方法针对舰船轴频电场谐波成分的特点,将谐波簇自适应线谱增强技术应用到舰船轴频电场的信号处理中,实验结果表明,线谱强度高于附近连续谱的强度[3]。包中华,龚沈光，李松等人提出基于自适应累量算法的舰船轴频电场信号检测方法，该方法利用高阶累量对高斯噪声的抑制能力，将自适应累量算法的滤波器对接收信号进行滤波,然后对滤波输出的信号进行滑动功率谱检测,但该方法有较大的输出延迟和较长的自适应收敛时间[4-5]。马育锋,龚沈光,姜润翔,张凡,李松等人提出基于小波变换的目标信号检测方法,该方法利用小波变换计算舰船轴频电场信号的功率谱,提取其特征量，然后对轴频电场信号进行滑动地目标检测[6-7]。

本文提出了一种数字信号处理的方法,利用舰船轴频电场是窄带周期信号的特性,利用离散的谐波小波变换结合最小均方(least mean square,LMS)法，通过自适应谱线增强器,无需噪声参考信号就能实时有效地将其从宽带背景噪声中分离出来,从而能大大提高舰船轴频电场的远程探测能力。

1 自适应去噪

自适应滤波,就是利用前一时刻已获得的滤波器参数等结果,自动地调节当前时刻的滤波器参数以适应信号和噪声未知的或随时间变化的统计特性,从而实现最优滤波。自适应去噪原理见图1。通常假定参考通道噪声m(n)是由主通道噪声p(n)经过一个传递函数为H(z)的系统的输出,自适应除噪的本质就是通过自适应算法估计出H(z)的逆,用m(n)逼近d(n)=s(n)+p(n)，而有用信号s(n)与噪声不相关,实际上自适应算法是用m(n)来逼近p(n),得到p(n)的估计值ˆp(n)，再与主通道d(n)=s(n)+p(n)相减以达到最大限度地消除主通道噪声p(n),获得有用信号s(n)的目的。自适应滤波器的权系数是由逼近误差e(n)通过某种自适应算法反馈调整的。min[e(n)]作为自适应滤波器调整权向量ωN的准则[8-13]。

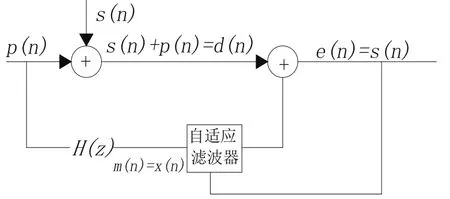
图1 自适应去噪原理Fig.1 Schematic diagram of adaptive denoise

2 自适应谱线增强

自适应谱线增强器最早是Windrow等人在1975年提出的。自适应谱线增强器已广泛应用于频谱估算、谱线估计以及窄带检测等领域[14-17]。在窄带信号加上宽带噪声信号的情况下,用自适应谱线增强方法无需独立的参考信号就能将有用窄带信号分离出来,其原理如图2所示。

自适应谱线增强器的核心部分是一个自适应噪声抵消器。设输入x(n)是一个窄带信号xN(n)和一个宽带噪声xB(n)的叠加，将输入x(n)延时∆后作为抵消器的参考输入。只要适当地选取延时使处理器上下两个通道的噪声去相关，而单频信号由于其周期性仍具有很好的相关性。自适应滤波器通过形成一个中心频率为单频正弦频率的窄带滤波器，使得延时通道输入中的噪声分量被抑制而正弦信号分量被增强，从而在求差过程中使直接输入通道与y(n)中的信号分量相抵消，输出的残差噪声功率最小。

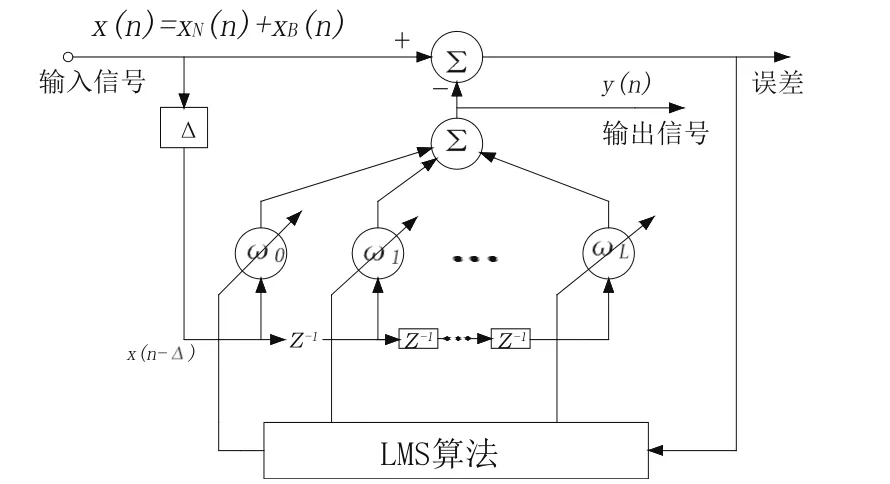
图2 基于LMS算法的自适应谱线增强原理Fig.2 Schematic diagram of adaptive line enhancement on LMS algorithm

3 谐波小波

当前正交小波的构造大多来源于多分辨分析的双尺度方程，一般没有明确的函数表达式，且相应频谱要随着小波系数的增加才越来越显示盒形特征。一种变换的盒形谱特性，它对于信号的处理是极为必要的。能否只用不多的小波系数构造出具有良好盒形谱特性的正交小波？正是从这一点出发，David E Newland进行了大量的工作，并于1993年从小波的频谱出发，成功地构造了具有严格盒形特征及简单的解析表达式的谐波小波(harmonic wavelet)[18]，而这正是来源于双尺度方程的伸缩小波(dilation wavelet)所缺乏的。

Newland从小波ψ(t)的Fourier变换ψ(ω)出发来构造小波。考虑实函数ψe(t)和ψo(t)（它们分别是变量t的偶函数和奇函数），分别定义它们的Fourier变换（频域）为

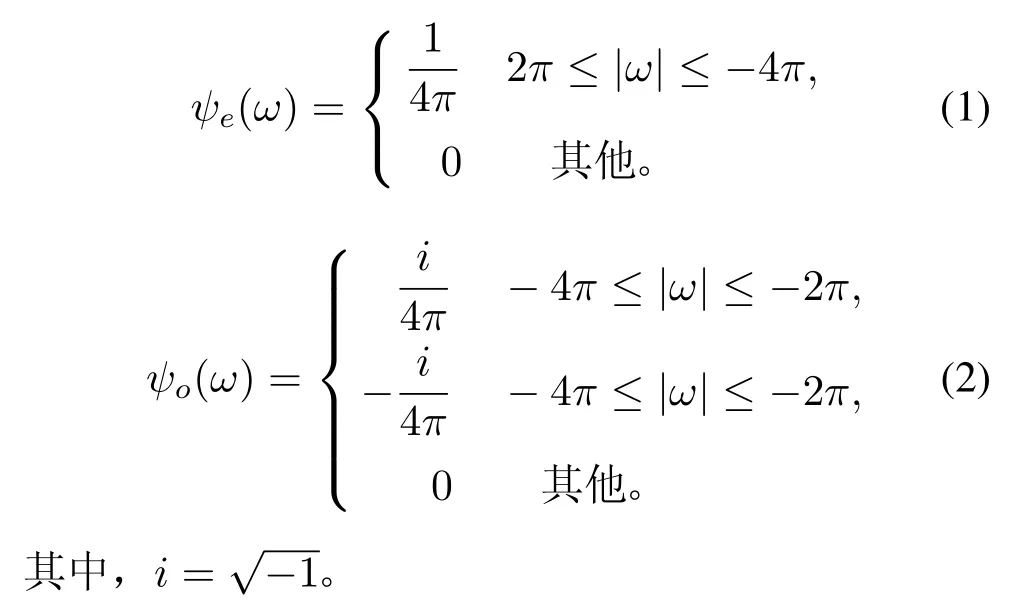
将它们组成复函数形式，有

分别对式(1)和式(2)作Fourier逆变换，可以得到它们的时域表达式为

为谐波小波，其实部与虚部如图3所示。由式(1)、式(3)，可以得到谐波小波的Fourier变换为

图3 谐波小波的实部与虚部Fig.3 The real part and imaginary part of harmonic wavelet

理想的谐波小波频谱如图4所示。

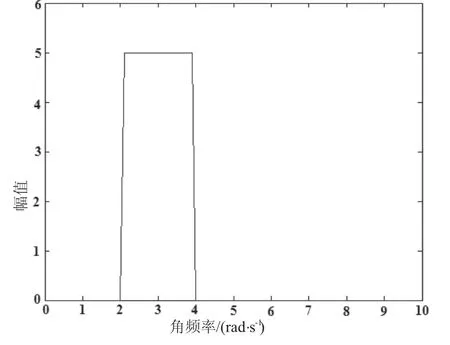
图4 理想的谐波小波频谱Fig.4 Perfect frequency spectrum of harmonic wavelet

从图4中可以看出，谐波小波的频谱具有良好的紧支特性以及严格的盒形特性，充分体现了构造者的初始构想。同时通过图3谐波小波的实部和虚部时域波形，我们会发现，谐波小波极佳的频域特性使其在时域上付出了一定代价。

为了得到谐波小波ψ(t)的二进伸缩平移系，可以用变量(2jt−k)（其中j,k∈Z）代换式(6)中的变量t，得到

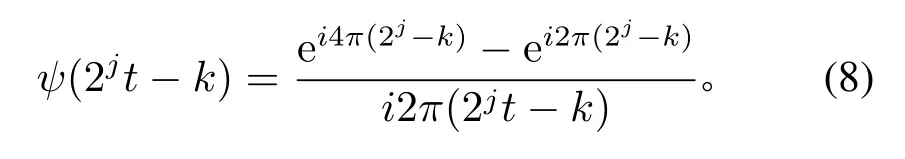
可以看到，小波的形状没有改变，但它在尺度方向上的尺度压缩了2j，并且其位置在新尺度上被平移了k个单位。j的值决定了小波的层或尺度：在j=0层，谐波小波的Fourier变换频带位于[2π,4π]；而在第j层，其频谱位于[2j+1π,2j+2π]之间。随着j的增大，其频谱带宽以二进的方式逐渐加大，如图5所示。

从频谱图5可以看出，谐波小波对信号的分析频宽从高频到低频是以1/2关系逐渐减小的，对信号的低频部分划分比较细，而高频部分划分比较粗，这说明谐波小波分解是一种小波分解。

谐波小波构成了L2(R)空间的规范正交基，则任何信号f(t)∈L2(R)都可表示为谐波小波的线性和，即

这也就是信号的谐波展开。αj,k为函数的小波展开系数

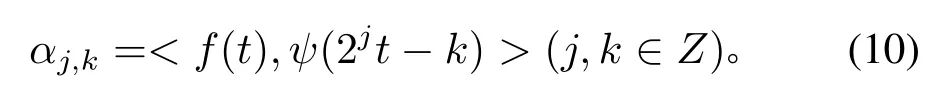
直接用求内积的方法计算小波展开系数运算量太大，很不实用。Newland教授给出了一种基于FFT的快速算法，可以快速而准确地求得谐波小波分解，从而也使得谐波小波运用于工程实践成为可能[19-22]。

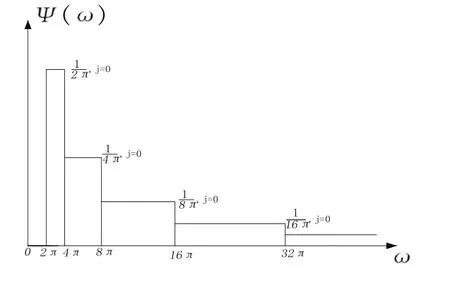
图5 不同层上谐波小波的频谱Fig.5 Frequency spectrum of harmonic wavelet on another levels

4 基于谐波小波的自适应谱线增强

由于传统的LMS在自适应信号处理中的不足，本文提出基于谐波小波的自适应谱线增强基自适应去噪方法。该方法利用多分辨率分析理论，把信号和噪声分解在不同的频率范围内，使信号和噪声的频谱得到简化，从而减少了自适应滤波器的级数[23-25]，使输入自相关矩阵阶数降低，与传统的LMS算法相比，基于谐波小波的自适应谱线增强算法的收敛速度和稳定性得到了显著的提高。

谐波小波是平方可积函数空间上的一簇基函数。任何平方可积的信号x(n)均可由谐波小波函数ψ(t)的伸缩和平移来表示，即

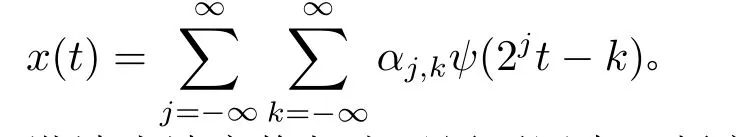
谐波小波变换相当于用不同中心频率(中心频率与带宽比值恒定)的滤波器，对输入信号进行分解。离散谐波小波变换(discrete harmonic wavelet transform,DHWT)是一种正交线性变换，变换系统可以通过快速的Newland算法获得。

自适应谐波小波滤波器原理图如图6所示。DHWT/LMS算法的步骤为：

1)离散谐波小波变换预处理抽头延迟输入；

2)用其功率的平方根对变换后信号进行标准化；

3)再把得到的等功率信号输入到一个自适应线性组合器中去，而这个自适应线性组合器的权系数是用LMS算法进行调整的。

对于这个算法，直交化步骤是不依赖数据的，而仅仅在功率标准化步骤依赖数据，也就是说，用于标准化信号的功率水平是由实际数据估计的。由于其各部分的简单性，这些算法保持了纯粹LMS算法的鲁棒性和较低的计算代价，同时也改进了收敛速率。

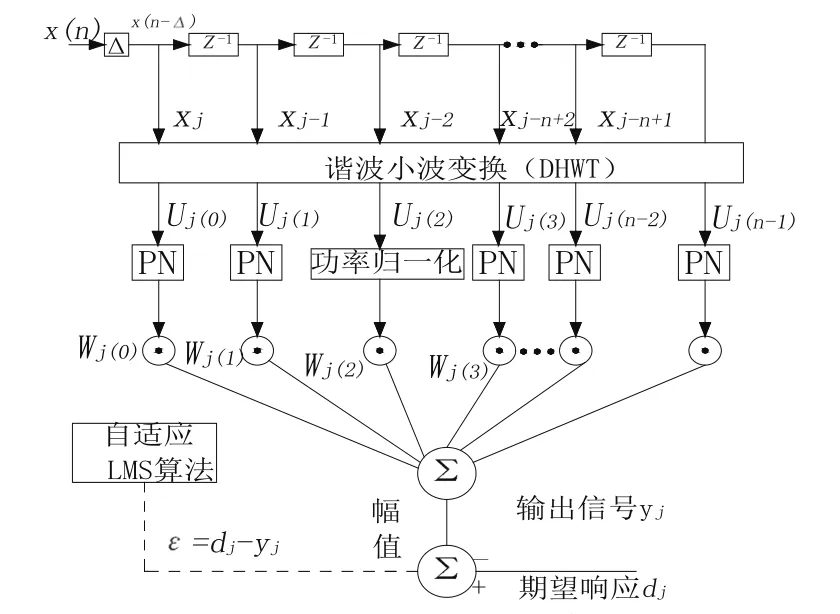
图6 自适应谐波小波变换LMS算法原理图Fig.6 Schematic diagram of LMS algorithm on adaptive harmonic wavelet

在L2(R)空间中，信号x(n)的小波级数重构为

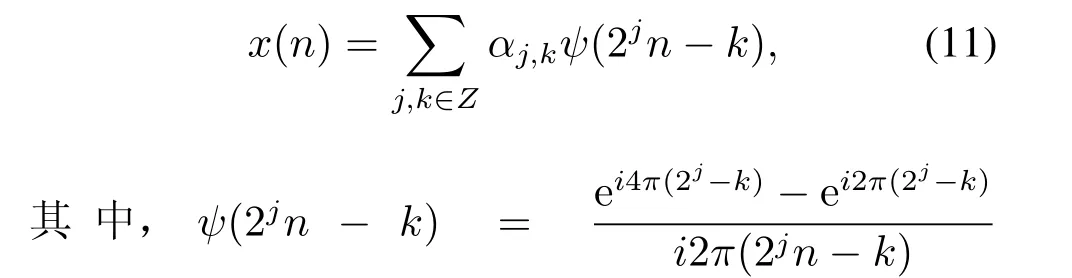
是L2(R)空间的一组正交小波基，j是尺度参数，k是时间中心参数，谐波小波系数

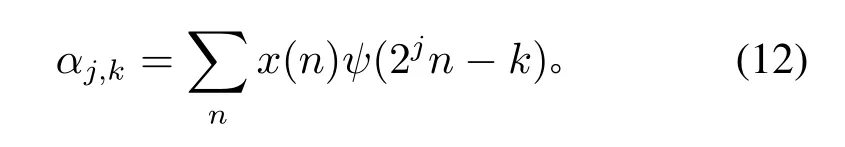
然而在实际应用中，式(11)可由下面的有限和去逼近无限和，即

输入信号投影到对应于不同尺度的正交子空间，谐波小波变换的目的就是生成在小波子空间中的投影的离散重构，也就是

令vj(n)是投影的逼近，即

式中，dj,k是谐波小波系数dαj,k的离散逼近。

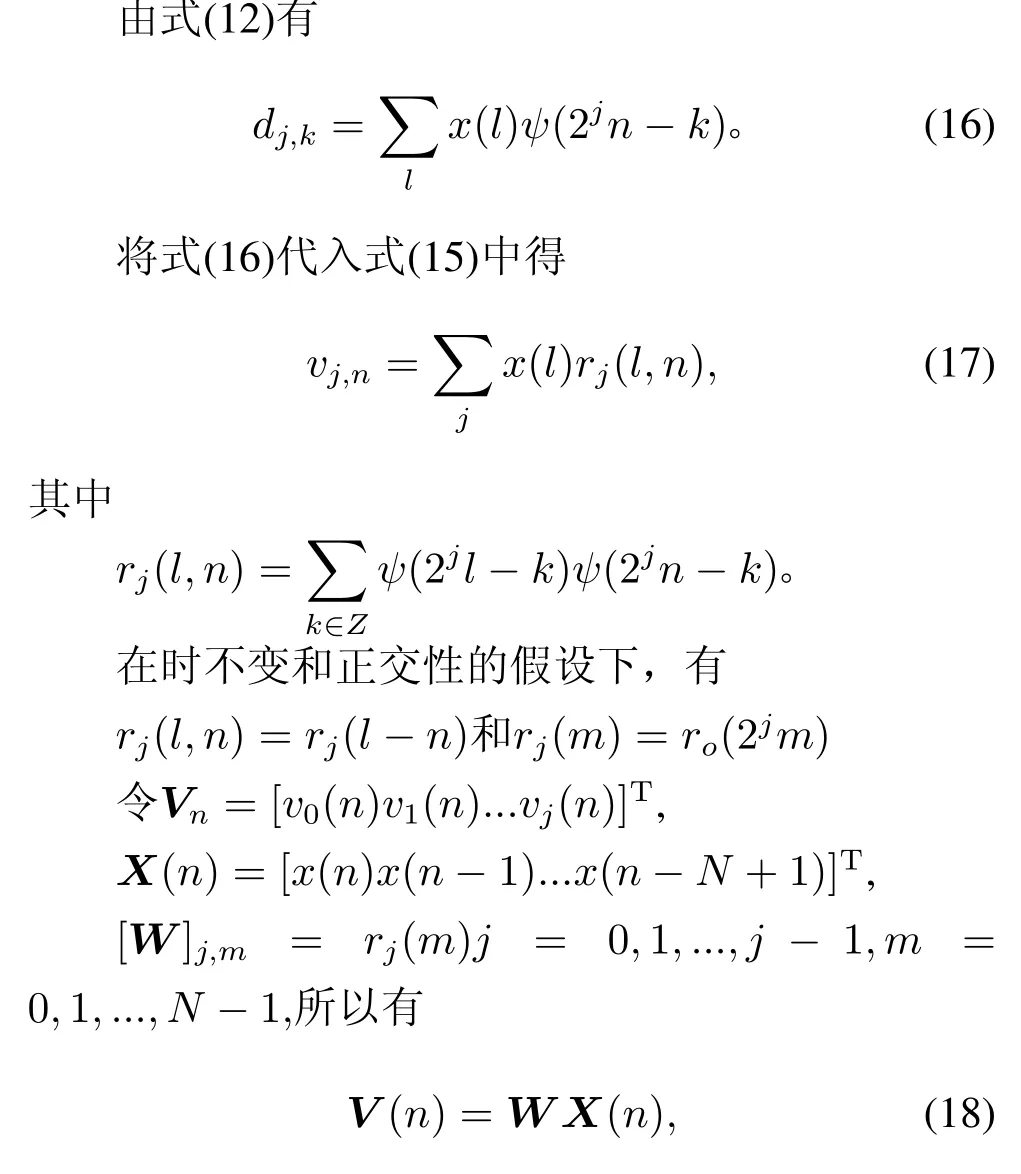
式中，W是N×J的DHWT谐波小波矩阵。

输出信号和误差信号分别为

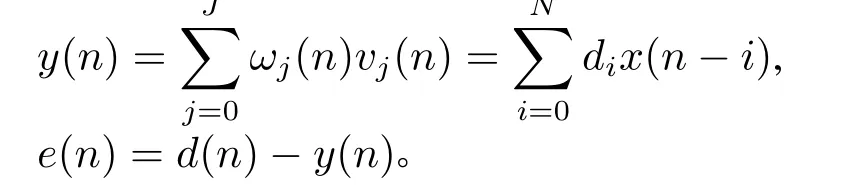
在DHWT/LMS算法滤波器，输入信号经谐波小波变化形成新的向量vj,通过滤波器的权向量ωj而形成滤波器的输出信号y(n)=，权系数更新算法为ωv,k+1= ωv,k+2µv,kεv,kUk,µv是常数或随时间可变的正整数，对均值和方差都收敛的一个较强的条件为

所以有下面的结论：在小波变换域的滤波器系数的Wiener解由ωvopt=(TT)ωopt给出，ωopt为在时域的Wiener解；同样均方(mean square error,MSE)误差的最小值在变换域与在时间域的值是一样的，εvmin= εmin。

对于采用常值收敛因子算法，DHWT变换前后的收敛条件是相同的，tr(RV)=tr(RX)，因此，对于满足收敛条件的常数因子能在时间域保证收敛；平均误差过调节也保持不变；时间常数τp=1/2µλp取决于最小特征值，其中只要{λp,1≤p≤N}为Rx或Rv的特征值，由于Rv=TRxTT并且T为正交阵，因此Rx与RV的特征值相同，从而LMS算法在变换前后有相同的收敛速度。若令收敛因子µv= γ,γ为一常数，直交化LMS算法变为ωv,j+1= ωvv,k+2γεvjvj收敛条件和平均误差调节为收敛速度将显著改善，且无论输入信号的统计特性如何，收敛仅由γ控制。控制收敛的还是特征矩阵和特征值。

5 仿真实验

5.1 实验方法

将1:100舰船缩比模型(螺旋桨的转速为180r/min)用铝制金属架固定在长、宽、深分别为8m、5m和1.5m的无磁性水池中，池中装有由工业盐调制的人造海水(电导率为3.66(Ω·m)−1)。用三维电场传感器分别测量轴频电场的横向、纵向和垂直方向上的分量，然后将测得的电位差由同轴电缆传送到虚拟仪器测量系统，然后将采集到的数据存入计算机。

5.2 仿真结果

根据实验情况及仿真轴频信号的特点，利用谐波小波对信号进行9层分解。

使舰船缩比模型船壳的下半部分和螺旋桨浸泡在水中，设定采样频率为1 000Hz，将三维电场传感器移动至距离船模200cm处，测量轴频电场结果如图7所示，频谱图如图8所示。

图7轴频电场信号Fig.7 Shaft-rate modulated electric fi eld signal

图8 轴频电场信号的频谱Fig.8 Frequency spectrum of Shaft-rate modulated electric if eld signal

从图7和图8中可以看出，轴频电场信号已经很难从环境噪声中分离出来。采用自适应谱线增强器，运用LMS算法对图7的数据进行处理后，得到的时域信号如图9所示。

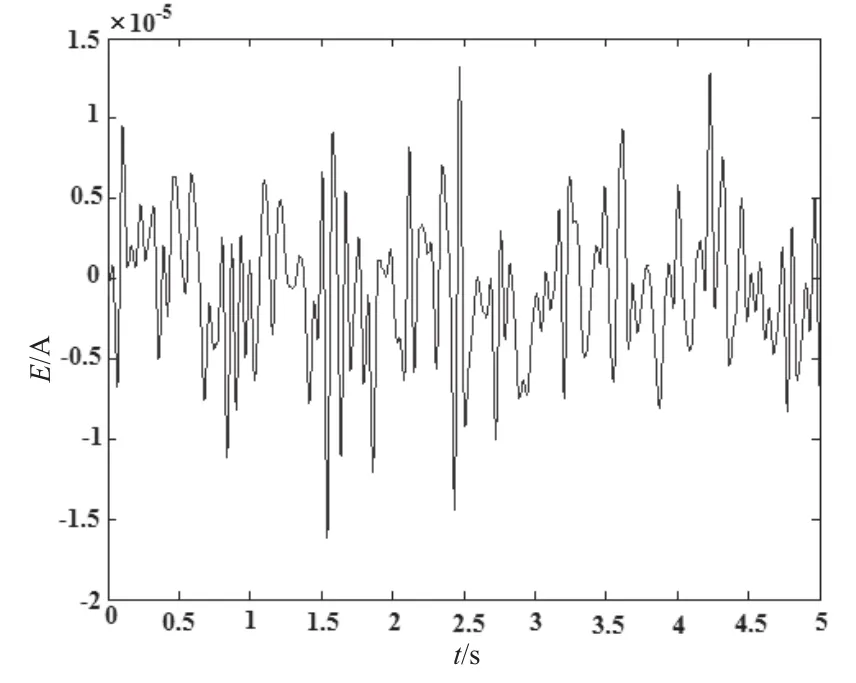
图9 经自适应谱线增强器处理后的信号Fig.9 Adaptive line enhancement signal

采用LMS算法自适应谱线增强处理后的信号频谱图如图10所示，采用基于谐波小波算法的自适应谱线增强处理后的信号频谱图如图11所示。

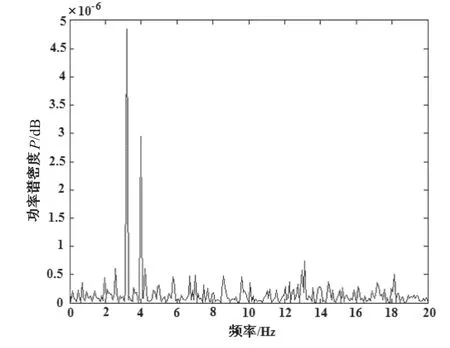
图10 LMS算法自适应处理后的信号频谱图Fig.10 Frequency spectrum of signal on LMS algorithm

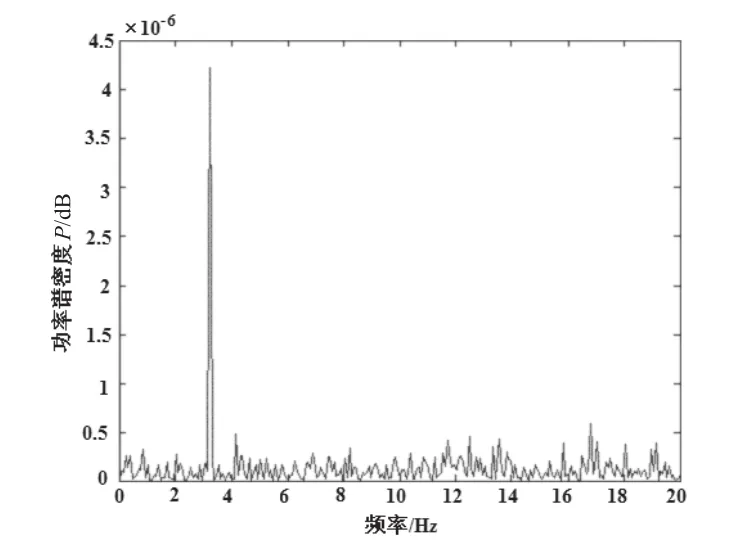
图11 基于谐波小波算法的自适应谱线增强处理后的信号频谱图Fig.11 Frequency spectrum of adaptive line enhancement signal on harmonic wavelet

比较图10和图11两图可以看出，采用基于谐波小波算法的自适应谱线增强处理后的信号频谱的特征较LMS算法自适应谱线增强处理后的信号频谱图信号比较明显，能够真正反映轴频电场的信号特征，也说明基于谐波小波算法的自适应谱线增强具有良好的频率选择特性。经过自适应谱线增强的数字处理后，能够很大程度地压制背景噪声，从中提取有用的轴频电场特征信号，该信号的特征为3Hz，证明该信号的特征与螺旋桨的转速成比例。

采用LMS算法的自适应迭代次数如图12所示，采用基于谐波小波算法的自适应谱线增强的自适应迭代次数如图13所示。

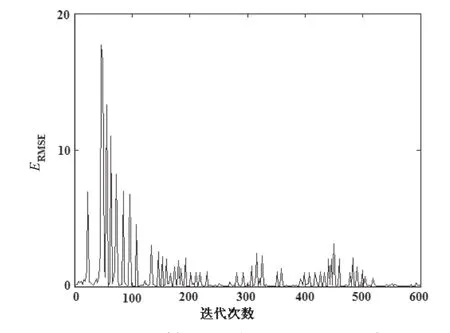
图12 LMS算法的自适应迭代次数Fig.12 Adaptive iterative degree of LMS algorithm

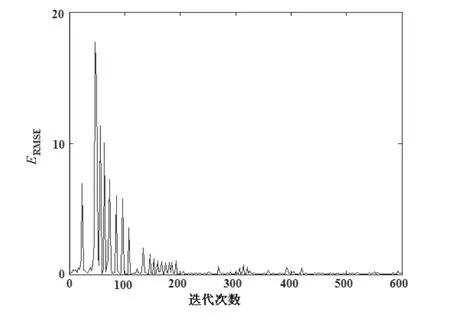
图13 谐波小波算法自适应迭代次数Fig.13 Adaptive iterative degree of harmonic wavelet algorithm

从图12和图13可见，采用基于谐波小波算法的自适应谱线增强的自适应迭代次数比采用LMS算法的自适应迭代次数少，说明采用基于谐波小波算法的自适应谱线增强能很好地收敛。

6 结语

利用自适应谱线增强的数字信号处理方法，结合具有良好的频率选择特性和紧支特性的谐波小波提出了基于谐波小波的自适应谱线增强器算法。该算法能够实时有效地将微弱的轴频电场特征信号从环境背景噪声中分离出来，大大提高了舰船轴频电场的检测能力，为在海洋中远程监测舰船轴频电场信号提供了一个简单而又实用的方法，同时该算法具有快速的收敛速度，使得谐波小波在变换域自适应算法中成为优选方案。

[1]毛伟,林春生,周萌.基于高阶FS谱对角切片的舰船轴频电场微弱信号检测方法[J].武汉理工大学学报:交通科学与工程版,2009,33(2) :325-328.

MAO Wei,LIN Chunshen,ZHOU Meng.Method to test the weak shaft-rate electric fi eld of the ship based on the diagonalsliceofFSpolyspectra[J].JournalofWuhanUniversity of Technology:Transportation Science＆Engineering,2009,33(2):325-328.

[2]HUANG Haibo,HUANG Xiaolin,ZHANG Gaoyu.Infrared small weak targets detection via high order cumulant harmonics estimation[C]//The 6th World Congress on Intelligent Control and Automation,June 21-23,2006,Dalian,China.2006:9660-9663.

[3]刘彦琼,岳瑞永,天作喜,等.基于谐波簇自适应线谱增强器的舰船轴频电场检测[J].装备环境工程,2011,8(2):29-32.

LIU Yanqiong,YUE Ruiyong,TIAN Zuoxi,et al.Ship shaft-frequency electric fi eld testing based on harmonic waves adaptive line enhancer[J].Equipment Environmental Engineering,2011,8(2):29-32.

[4]龚沈光,卢新城.舰船电场特性初步分析[J].海军工程大学学报,2008,20(2):1-4.GONG Shenguang,LU Xincheng.Pilot study of electric fi eld characteristics of warsh[J].Journal of Naval University of Engineering,2008,20(2):1-4.

[5]马育锋,龚沈光,姜润翔,等.基于小波变换的目标信号检测方法[J].数据采集与处理,2009,24(6):789-791.

MA Yufeng,GONG Shenguang,JIANG Runxiang,et al.Detection method for target signal based on wavelet transform[J].Journal of Data Acquisition and Processing,2009,24(6):789-791.

[6]何振亚.自适应信号处理[M].北京:科学出版社,2002:19-22.

[7]Simon Haykin..自适应滤波器原理[M].4版.北京:电子工业出版社,2002:23-26.

[8]王卫红,姚志超,郑连强.三轴飞行仿真转台自适应复合控制方法[J].电机与控制学报,2011,15(9):74-79f3d06.

WANG Weihong， YAO Zhichao， ZHENG Lianqiang.Adaptive compound control method for the three-axis fl ight simulator[J].Electric Machines and Control,2011,15(9):74-79.

[9]徐飞,史黎明,李耀华.一种自适应补偿死区的异步电机参数测量方法[J].电机与控制学报,2012,16(10):1-6f3d06.

XUFei,SHILiming,LIYaohua.Measurementofinduction motor parameters by adaptive compensation for dead-time effect[J].Electric Machines and Control,2012,16(10):1-6.

[10]郭黎利,赵冰.多频带自适应脉冲设计[J].哈尔滨工程大学学报,2011,32(6):825-829.

GUO Lili,ZHAO Bing.Multiple adaptive pulse waveform design[J].Journal of Harbin Engineering University,2011,32(6):825-829.

[11]张兴福,黄少滨.自适应近邻的局部线性嵌入算法[J].哈尔滨工程大学学报.2012,33(4):f3d06489-495.

ZHANG Xingfu,HUANG Shaobin.Adaptive neighborhoods based locaIly linear embedding algorithm.[J].Journal of Harbin Engineering University,2012,33(4):f3d06489-495.

[12]张贤达.现代信号处理[M].北京:清华大学出版社,1998:42-46.

[13]胡广书.数字信号处理—理论、算法与实现[M].北京:清华大学出版社,1998:50-52.

[14]WIDROW Stearns S D.Adaptive noise canceling:principles and application[J].Proceedings of the IEEE,1975,6(2):1692-1716.

[15]姚天任,孙洪.现代数字信号处理[M].武汉：华中理工大学出版社,1999:78-84.

[16]NEWLAND D E.Harmonic wavelet analysis[J].Proc R Soc Lond A,1993,443(10):203-205.

[17]何正嘉，訾艳阳.机械设备费非平稳信号的故障诊断原理及应用[M].北京:高等教育出版社,2001:43-45.

[18]李方.谐波小波在设备故障诊断中的应用[D].武汉:武汉科技大学机械自动化学院,2005:13-15.

[19]高珍.齿轮损伤的谐波小波分析方法研究[D].太原:太原理工大学机械工程学院,2005:43-46.

[20]ERDOL N,BASBUG F.Wavelet transforem based adaptive fi lters:analysis and new results[J].IEEE Transactions on Signal Processing,1996,44:2163-2171.

[21]DOROSLOVACKI M I,FAN H.Wavelet-based linear system modeling and adaptive fi ltering[J].IEEE Transactions on Signal processing,1996,44:1156-1167.

[22]HOSUR S,TEWFIK H.Wavelet domain adaptive FIR fi lter-ing[J].IEEE Transactions on Signal Processing,1997,45:617-630.

[23]徐飞,史黎明,李耀华.一种自适应补偿死区的异步电机参数测量方法[J].电机与控制学报,2012,16(10):1-6.f3d06

XUFei,SHILiming,LIYaohua.Measurementofinduction motor parameters by adaptive compensation for dead-time effect[J].Electric Machines and Control,2012,16(10):1-6.

[24]史晓陶.海洋环境交变电场变化规律研究[J].装备环境工程,2011,8(6):100-103.

SHI Xiaotao.Research on variable pattern of alternative electric fi eld of marine environment[J].Equipment Environmental Engineering,2011,8(6):100-103.

[25]包中华,龚沈光,李松.基于自适应累量算法的舰船轴频电场信号检测方法[J].海军工程大学学报,2009,21(4):13-16.

BAOZhonghua,GONGShenguang,LISong.Ashipshaftrate electric signal detection method based on adaptive cumulant algorithm[J].Journal of Naval University of Engineering,2009,21(4):13-16.

(编辑：张诗阁)

Adaptive line enhancement based on harmonic wavelet and application research

ZHAO Jing-bo,LIU Hui-min,ZHANG Lei
(School of Automation Engineering,Qingdao University of Science and Technology,Qingdao 266520，China)

With the rapid attenuation of extremely low frequency fi eld due to the increasing transmission distance,the fi eld is readily covered by environmental noises.In view of this,an algorithm was then advanced to improve the capability of remotely detecting the extremely low frequency(ELF) fi eld by virtue of the harmonic-wavelet adaptive line enhancer.This algorithm was used to process the actual measured data of the shaft-rate modulated electric fi eld produced by use of vessel’s physical scale models,whose results demonstrate that the algorithm effectively separated the weak characteristic signals of shaft-rate modulated electric fi eld from the environmental noises at real time,greatly improving the capability of detecting a vessel’s shaft-rate modulated electric fi eld.In view of the facts and the characteristics of simulated signals,harmonic wavelets were used to decompose the signals into 9 layers.In the meanwhile,there were less adaptive iterations due to the adaptive line enhancement obtained by the harmonic wavelet algorithm than by the least mean square algorithm.This indicates that the adaptive line enhancement based on the harmonic wavelet algorithm is able to converge at higher rate.f3d06

shaft-rate electric fi eld;wavelet;harmonic wavelet;adaptive;line enhancement

TM 46

A

1007–449X(2013)10–0077–08

2013–03–01

山东省高等学校科技计划项目(J12LN37);泰山学者海外特聘专家项目(C2010-T005);山东省自然科学基金项目(ZR2013FM014)

赵景波(1971—),男,博士,副教授,硕士生导师,研究方向为信号处理和控制理论;

刘慧敏(1989—),女,硕士研究生,研究方向为控制理论;

张 磊(1990—),男,硕士研究生,研究方向为控制理论。

赵景波