大型异步电机定子端部绕组电磁力的研究

鲍晓华，程晓巍，方勇，吕强，单丽

(1.合肥工业大学 电气与自动化工程学院，安徽合肥 230009;2.合肥恒大江海泵业股份有限公司，安徽合肥 231131)

大型异步电机定子端部绕组电磁力的研究

鲍晓华1，程晓巍1，方勇1，吕强1，单丽2

(1.合肥工业大学 电气与自动化工程学院，安徽合肥 230009;2.合肥恒大江海泵业股份有限公司，安徽合肥 231131)

针对大型异步电机定子端部绕组受电磁力作用容易发生故障的实际工程问题，提出了一种通过改变端部绕组锥度角进而改善定子端部绕组力学性能的方法。利用MAXWELL方程结合分离变量法推导出了端部绕组磁场的表达式，通过时步有限元方法建立端部绕组模型，进而分析绕组端部磁场的分布情况。最后结合洛伦兹法则，利用局部坐标变换得到端部绕组斜线段电磁力的计算公式，运用数值分析方法对其仿真分析，在此基础上结合具体算例，对比分析了端部绕组在不同锥度角下电磁力的分布情况。分析结果表明，该方法能够改善端部绕组的力学性能，延长电机使用寿命，为干式潜水电机定子端部绕组的优化设计提供理论依据。

潜水电机;有限元方法;锥度角;端部绕组磁密;电磁力密度

0 引 言

大型异步电机广泛应用于关系到国民经济的重要场合，种类很多，高压潜水电机是其中重要的一种，广泛应用于江河湖泊中取水、农业排灌、城市或工厂的污水处理、矿山给排水、海上采油平台抽取海水等重要场合，在国内需求不断增加的刺激下，潜水电机向大型化、高功率化的方向发展，因此定子绕组端部承受的电磁力也越来越大。电机在长期运行过程中，定子绕组端部承受强大的、周期性的电磁力作用，在其作用下所引发的电磁振动是导致绕组疲劳断裂和引线绝缘磨损的主要原因之一[1-2]，特别是发生短路故障时，作用在定子绕组端部的电磁力超过额定运行状态下的100倍，造成的危害及其严重。因此对定子端部绕组电磁力进行理论研究[3-4]和优化计算，以便对干式潜水电机端部绕组提供更加合理的设计方案，提高电机运行的安全稳定性，具有非常要的理论意义。

近年来，国内外的专家学者对电机定子绕组端部电磁力进行了较为广泛的研究。文献[5-6]在忽略端区结构影响的基础上，运用有限差分法分别计算了电机在运行稳定状态和瞬时状态下大型发电机定子端部绕组所受到的电磁力。文献[7]在文献[5-6]的基础上针对大型异步电动机，采用有限元分析方法着重分析了电磁力的正弦分量对端部绕组的影响，忽略了其恒定分量的作用。文献[8]仅考虑了由转子电流激发的磁场对鼠笼型电机端部绕组所受电磁力的影响。R.Albanese等人在考虑到定转子电流、铁磁饱和等因素的影响下，采用非线性积分公式法阐述了绕组端部电磁力的计算思路，以及定子绕组在电磁力的作用下发生的位移变化[9]，但是该方法产生较大的计算误差。文献[10]对定子端部绕组整体结构的动力问题进行了研究，推导了定子端部绕组整体振动控制方程，以及所受电磁力的表达式，并且通过数值计算得到了端部绕组的固有振动频率、电磁力及动力响应的计算结果。文献[11]针对具体实例，考虑到定转子铁心端部的影响，运用有限元方法分析了磁场在定子绕组端部区域的分布情况，进而更为精确地计算出端部各区域中电磁力密度的动态响应。以上各文献在计算电机定子绕组端部电磁力方面取得了一定的成果，具有一定的实用价值。但是针对电磁力对端部绕组的破坏，并没有提出相应的改进办法用以减弱电磁力对绕组端部的影响。

本文在前人研究的基础上针对干式潜水电机（1000 kW/10 kV）建立绕组端部模型，通过有限元方法对定子绕组端部电磁场进行分析，在得到磁感应场强度分布的基础上，运用数值分析方法结合具体算例对绕组端部所受电磁力进行计算分析，提出了一种通过改变端部绕组锥度角进而改善绕组端部所受电磁力的方法，最后对不同的角度所对应的电磁力进行仿真计算。

1 定子绕组端部磁场的分析

1.1 绕组端部磁场的产生

定子绕组端部区结构复杂，如图1所示，其磁场是由分布复杂的绕组端部电流所产生，又受到形状复杂、材料不同的端部结构件的影响，致使端部磁场的计算极为困难。通常仅考虑一些主要结构件（定子铁心压板、端盖、机座壁和转轴等）的影响，并认为这些结构件的形状是规则的圆筒或平面；同时忽略其中的涡流阻尼效应，把它们看作µ为无穷大，σ为零的理想磁镜面。

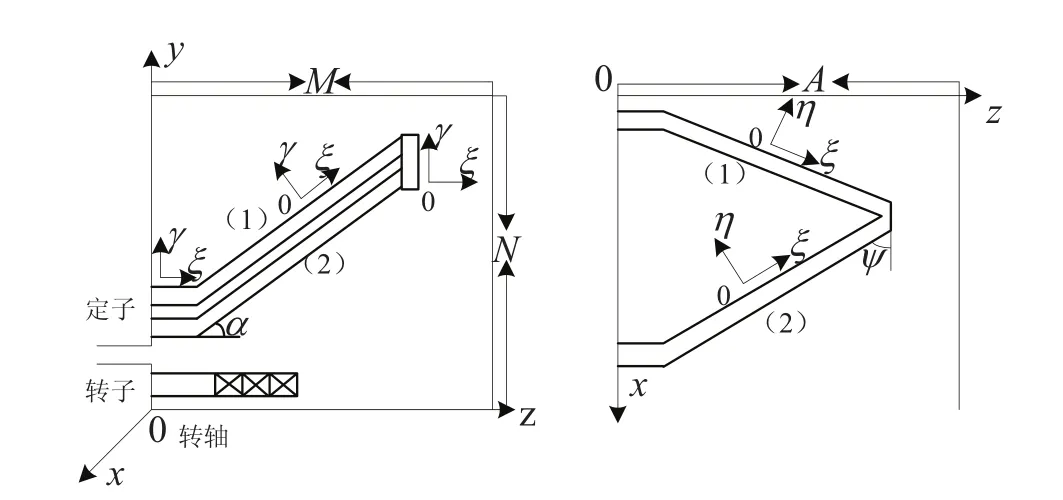
图1 端部绕组结构Fig.1 Structure of end winding

绕组端部区域是由分属于各相的许多线圈组成构成，由于端部磁场主要由端部绕组斜线段电流产生，因此为求端部电磁场，将每层中属于同一相绕组的斜线段电流密度沿x、y、z轴展成傅里叶级数。然后将三相叠加，得同一层绕组电流的表达式[12]。

斜线伸出段外层（1）段：

在直角坐标系下，通过给出的电流密度展开式，依据麦克斯韦方程组，即

式中：A(Ax,Ay,Az)为矢量磁位；J(Jx,Jy,Jz)为电流密度矢量；B(Bx,By,Bz)为磁感应强度矢量；∇2为拉普拉斯微分算子；∇为哈密顿算子。

采用分离变量法对式（5）进行求解，将电流产生的磁场进行叠加，最终得到内外层绕组磁感应强度的表达式为

图2 启动过程中磁感应强度在绕组端部的分布Fig.2 End-winding’s magnetic fl ux density distribution of starting state

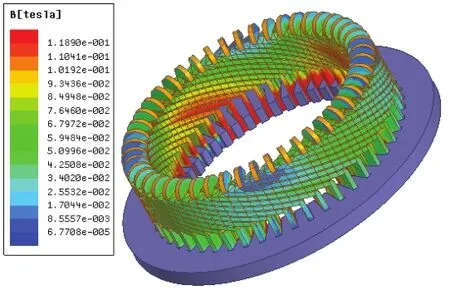
图3 稳定运行过程中磁感应强度在绕组端部的分布Fig.3 End-winding’s magnetic fl ux density distribution of steady state

1.2 端部磁场仿真分析

由于绕组端部结构复杂，二维有限元分析难以达到实际的工程要求，因此通过软件建立三维有限元模型可以精确地进行计算和仿真。通过FEM分析软件计算磁感应强度在电机定子绕组端部的分布情况，仿真结果如图2和图3所示。

图2和图3分别表示干式潜水电机在起动和稳定运行过程中，A相电流达到最大值时磁感应强度在绕组端部的分布情况。从图中可以看出起动状态下磁感应强度比稳定运行时磁感应强度大,同时磁感应强度在A相所属绕组端部斜线段的分布比较集中，因此较之绕组端部其他部位，斜线段所受的电磁力比较大。当B相、C相电流达到最大值时，可得到相同的结论，即电磁力主要集中分布于绕组端部斜线段部位。

2 定子绕组端部电磁力的分析

2.1 绕组端部电磁力的数值计算

电机绕组端部的振动是在电磁力激发下进行的，同时绕组的疲劳、断裂破坏等问题也均与电磁力有关系。因此，绕组端部电磁力的数值计算是干式潜水电机运行安全性和可靠性的重要前提。

如图1所示，为求单根绕组所受电磁力，在绕组线棒的局部坐标系(ξ,η,γ)下，结合洛伦兹力公式可得

式中：J(Jξ,Jn,Jγ)为绕组传导的电流密度矢量；B(Bξ,Bη,Bγ)为经过坐标变换后的各段磁感应强度；i,j,k分别为沿坐标ξ,η,γ,方向的单位矢量，而由传导电流引起的电磁力密度矢量为F(Fξ,Fη,Fγ)。

电磁力主要集中分布于绕组端部斜线段，由传导电流引起的电磁力密度分量在内外层绕组斜线段的表达式为

内层：

式中：Im为绕组电流的幅值；ϕ0=0◦,120◦,240◦分别对应于电机三相电流的相角；Q1∼Q4为坐标和B(Bξ,Bη,Bγ)的函数[13]；上标n和w分别表示绕组的内层和外层。

2.2 端部绕组电磁力的仿真分析

针对干式潜水电机（1 000 kW/10 kV）的实际运行情况，结合式(8)∼式(13)，通过数值分析方法，在实际算例的基础上，给出绕组端部所受电磁力密度的仿真结果。

图4∼图7分别给出了绕组端部斜线段内、外层绕组所受磁力密度随时间和坐标变化的三维图。由图可见内外层电磁力密度随时间作周期性变化，并且随坐标ξ变化的过程中，三维曲线具有不同的峰值，对应不同的最大正、负值。对斜线段内层绕组而言，沿ξ的分布主要集中于0.13∼0.19m范围内，靠近绕组鼻端。在ξ=0.16m处取得正向最大值为13.6 N/m，负向最大值为29.7 N/m。对斜线段外层绕组而言，沿ξ的分布主要集中于0.15∼0.21m范围内，同样靠近绕组鼻端，在ξ=0.18m处取得正向最大值为37.8 N/m，负向最大值为17.5 N/m。由此可见，电磁力主要集中分布于绕组端部斜线段上的0.13∼0.21m范围内。

图4 斜线段内层电磁力密度随时间t和坐标ξ的变化图Fig.4 The electromagnetic forces density of inner slant partchange with time t and coordinate ξ

图5 斜线段内层电磁力密度随时间t和坐标ξ的变化图Fig.5 The electromagnetic forces density of inner slant partchange with time t and coordinate ξ

图6 斜线段外层电磁力密度随时间t和坐标ξ的变化图Fig.6 The electromagnetic forces density of outer slantpart change with t time and coordinate ξ

图7 斜线段外层电磁力密度随时间t和坐标ξ的变化图Fig.7 The electromagnetic forces density of outer slant part change with time t and coordinate ξ

3 端部绕组力学性能的改进

由以上结论可知，电磁力在斜线段上主要集中分布于0.13∼0.21 m的范围内，并且在0.16 m和0.18m处取得极值。为减少电磁力对端部绕组的影响，提出了一种方法，通过改变直线段与斜线段夹角α（如图1所示）进而改善端部绕组的力学性能。因此在数值算例(α=21.7◦)的基础上，分别给出了一个周期内不同角度下对应的电磁力密度在斜线段0.16 m和0.18 m处的变化规律。在数值算例(α=21.7◦)的基础上，工程要求允许范围内，每隔3◦取一个角度，得到不同角度下电磁力密度随时间的变化规律。

图8和图9表示内层绕组电磁力密度在不同的角度下随时间变化的曲线，由图可知电磁力曲线近似地呈正弦规律分布。α=27.7◦对应的曲线幅值较之其它角度下的曲线幅值大，正向最大值为15.9 N/m，负向最大值为33.7 N/m。α=19.7◦时对应的曲线幅值较之其他角度下的幅值小，正向最大值为11.7 N/m，负向最大值为27.2 N/m。因此两个角度下曲线对应的幅值分别相差为4.2N/m和6.5N/m。图10和图11为外层绕组电磁力密度变化规律，且电磁力的分布曲线近似呈余弦规律分布。当α=27.7◦时，曲线对应的正向幅值较之其他角度下的幅值大，其大小为38.4 N/m。当α=24.7◦时，曲线对应的负向幅值较之其他角度下的幅值大，大小为14.3 N/m。但当α=19.7◦时，曲线对应的正向幅值和负向幅值都是最小，分别为28.3 N/m和8.8 N/m，因此正向幅值和负向幅值分别相差为10.1 N/m和5.5 N/m。

图8 不同角度下内层绕组电磁力密度在ξ=0.16m处随时间的变化图Fig.8 The forces density at ξ=0.16m of inner slant part change with time t corresponding different angles

图9 不同角度下内层绕组电磁力密度在ξ=0.16m随时间t的变化图Fig.9 The forces densityat ξ=0.16m of inner slant part change with time t corresponding different angles

图10 不同角度下外层绕组电磁力密度在ξ=0.18m随时间t的变化图Fig.10 The forces density at ξ=0.18m of outer slant part change with time t corresponding different angles

图11 不同角度下外层绕组电磁力密度在ξ=0.18m随时间t的变化图Fig.11 The forces densityat ξ=0.18m of outer slant part change with time t corresponding different angles

综上所述，α=19.7◦时对应的电磁力密度幅值相对于其他角度下的电磁力密度幅值小，整体的变化趋势相对来说比较平缓，由此可以减弱因电磁力作用而引起的端部电磁振动强度，进而降低端部绕组事故的发生率，延长电机使用寿命。

4 结论

本文针对干式潜水电机端部绕组易发生故障的实际工程问题，提出了一种通过改变绕组端部倾斜角α的方法改善端部绕组的力学性能。通过局部坐标变换法，详细分析了电磁力密度在端部绕组斜线段上的分布规律，在此基础上改变端部绕组锥度角α的大小，得出了不同角度下电磁力密度在斜线段上随时间的分布图。综上所述，可得到以下结论：

1）电磁力密度在绕组端部斜线段上随坐标和时间呈周期性变化，主要集中分布于端部绕组斜线段的后半段0.13∼0.21 m范围内。

2）在工程允许的范围内，改变斜线段倾斜角对端部绕组力学性能进行优化分析，通过对比计算得到当α=19.7◦时，电磁力密度的幅值在数值算例的基础上降低了9.5 N/m，达到了预期的效果。

该方法综合运用了电磁场有限元、数值分析等计算手段，有效地分析了工程中的实际问题，具有较高的计算精确度，对干式潜水电机端部绕组的优化设计具有较大的参考意义和实用价值。

[1]LIN Ranran,LAIHO Antti Nestori,HAAVISTO Ari,et al.End-winding vibrations caused by steady-state magnetic forces in an induction machine[J].IEEE Transactions on Magnetics,2010,46(7):2665-2674.

[2]MORI D,ISHIKAWA Takeo.Force and vibration analysis of induction motors[J].IEEE Transactions on Magnetic,2005,41(5):1948-1951.

[3]SHALLY D,FARRELL M,SULLIVAN K.Generator end winding vibration monitoring[C]//Proceedings of the Universities Power Engineering Conference,September 1-4,2008,Padora,Italy.2008:4651488.

[4]KIM Ki-Chan,LEE Hyung-Woo,CHUN Yon-Do,et al.Analysis of electromagnetic force distribution on end winding for motor reliance[J].IEEE Transactions on Magnetics,2005,41(10):4072-4074.

[5]SCOTT D J,SALON S J,KUSIK G L.Electromagnetic forces on the armature end windings of large turbine generatorsⅠsteady state conditions[J].IEEE Transactions on Magnetics,1981,PAS-100(11):4597-4603.

[6]SALON S J,SCOTT D J,KUSIK G L.Electromagnetic forces on the armature end windings of large turbine generatorsⅡTransientconditions[J].IEEETransactionson Power Apply,1983,34(7):14-19.

[7]LIN Ranran,ARKKIO Antero.3-D fi nite element analysis of magnetic forces on stator end-windings of an induction machine[J].IEEE Transactions on Magnetics,2008,44(11):4045-4048.

[8]WILLIAMSON S,ELLIS M R E.In fl uence of rotor currents on end-winding forces in cage motor[J].IEE Proceedings B:Electric Power Applications,1988,135(6):371-379.

[9]ALBANESE R,CALVANO F,MUT G D,et al.Coupled three dimensional numerical calculation of forces and stresses on the end windings of large turbo generators via integral formulation[J].IEEE Transactions on Magnetics,2012,48(2):875-878.

[10]胡宇达，邱家俊，卿光辉，等.大型汽轮发电机定子端部绕组整体结构的电磁振动[J].中国电机工程学报，2003，23(7):93-98.

HU Yuda,QIU Jiajun,QING Guanghui,et al.Electromagnetic vibration of integrity end winding of large turbogenerator stator[J].Proceedings of the CSEE,2003,23(7):93-98.

[11]STANCHEVA Rumena D,IATCHEVA Ilona I.3-D Electromagnetic force distribution in the end region of turbogenerator[J].IEEETransactionsonMagnetics,2009,45(3):1000-1003.

[12]李京平,唐任远.汽轮发电机定子端部绕组电动力研究[J].沈阳工业大学学报,1991,13(2):13-25.

LI Jingping,TANG Renyuan.The study of the electromagnetic forces on the end windings of stator in turbogenerators[J].Journal of Shenyang Polytechnic University,1991,13(2):13-25.

[13]汤蕴璆，梁艳萍.电机电磁场的分析与计算[M].北京：机械工业出版社，2010.

(编辑：于双)

Research on electromagnetic force in the stator end winding of large induction motor

BAO Xiao-hua1，CHENG Xiao-wei1，FANG Yong1，LU¨Qiang1，SHAN Li2
(1.School of Electrical Engineering and Automation,Hefei University of Technology,Hefei 230009，China;2.Hefei Hengda Jianghai Pump Co.,Ltd.,Hefei 231131,China)

According to the engineering problems produced by electromagnetic force of end winding in large induction motor,a method that changes taper angle of the end winding to improve the mechanical properties was proposed.Firstly,the magnetic fi eld expression in the region of end winding was derived by adopting the separation of variables method based on Maxwell equations,and then the magnetic fi eld distribution of the end winding was analyzed by Finite Element Method.Finally,combined with Lorentz rule and the local coordinated transformation,the electromagnetic force calculation formula of the end winding was derived,and the simulation of electromagnetic force was done by numerical recipes method.In combination with speci fi c examples of large dry submersible motor,different electromagnetic force distributions were derived by changing the taper angle of the stator end-winding.The simulation results show that the method improves the end winding’s mechanical properties effectively,prolongs the service life of motor and provides fundamental theory for the optimization design of stator end winding.

submersible motors; fi nite element method;taper angle; fl ux density of end-winding;electromagnetic force density

TM 46

A

1007–449X(2013)10–0027–06

2013–01–14

国家自然科学基金(51377039,51177033);中央高校基本科研业务专项基金(2012HGZY0003)

鲍晓华(1972—),男,博士,教授,研究方向为电机设计理论和技术、电机电磁场理论分析及计算;程晓巍(1988—),男,硕士研究生,研究方向为电机电磁场分析与计算、电机绝缘系统;

方 勇(1989—),男,硕士研究生,研究方向为电机电磁场计算;

吕 强(1988—),男,硕士研究生,研究方向为电机设计理论及电磁场分析;

单 丽(1964—),女,高级工程师,研究方向为电机制造与控制。

鲍晓华