基于小波神经网络的空气污染指数预报
李四海,魏邦龙,李爱英
(1.甘肃中医学院 公共课部,兰州 730000;2.兰州城市学院 信息工程学院,兰州 730070;3.兰州市经济管理干部学校,兰州 730083)
0 引言
大气污染物浓度的变化主要受同期气象条件的影响,研究气象条件与大气污染之间的关系对于大气质量预报及控制具有重要作用。近年来,小波分析及BP神经网络被广泛应用于气象因子与污染物浓度之间的非线性建模。小波分析用于对空气污染指数和大气污染物浓度时间序列进行多尺度分解,以发现序列的趋势性及局部波动性和随机性[1]。BP神经网络则用于建立气象因子与大气污染物SO2、NOx、可吸入颗粒物PM10等之间的非线性映射[2-3],但是单纯以气象因子作为网络输入,基于BP预报空气污染指数时,在时间序列非平稳段的预测精度不高且网络的收敛速度慢。
该文结合小波分析的多分辨率性质和人工神经网络的自学习、非线性逼近能力,提出了一种新的空气污染指数预报模型,小波神经网络模型(Wavelet Neural Network)。该模型应用小波的特征提取能力,提取时间序列在不同系列小波焦距下的高低频信息。以各尺度上的小波系数序列和重要的气象因子为输入,对兰州地区的空气污染指数进行实例预报,结果表明模型具有较高的预测精度,用于空气污染指数预报具有可行性和有效性。
1 影响空气污染指数的气象因子
研究表明[4],静风、逆温是构成兰州大气污染的基础原因,由于静风、逆温频率高,造成大气的稳定度高,这又进一步加剧了该市冬季的大气污染。
空气污染指数通常是根据SO2、NO2、PM10的浓度计算得出,根据计算结果的不同将空气质量分为优、良、轻度污染、中度污染、重度污染五个级别。研究表明,这三种污染物浓度与平均风速、平均温度呈负相关,与相对湿度呈正相关[5]。
根据以上分析,以最高温度、最低温度、平均风速及相对湿度作为小波神经网络的第一组输入。
2 小波神经网络预报模型
2.1 离散小波变换
小波分析是一种非平稳信号分析方法,通过一个基本小波的伸缩和平移构成一系列小波函数用于对信号进行多尺度逼近和分析。小波变换具有良好的时频局部化能力,能够将信号分解为任意系列频带的直和,享有信号处理的“数学显微镜”美誉。
设信号f(t)在Vj空间中的离散采样序列为f(k),k=0,1,2,…,n-1,则Mallat小波分解算法为:

其中cj,k和dj,k分别为信号的低频和高频部分,h(n)和g(n)分别为低通滤波器H和高通滤波器G的系数,且gn=(-1)nh1-n
Mallat重构算法为:

2.2 小波神经网络预报模型
2.2.1 小波特征提取
小波具有许多良好的性质,如消失矩、正交性等,小波变换常用于去噪、压缩及特征提取。该文选用db3小波,使用Matlab7.1中的小波工具箱对2011.4.21-2012.4.20的空气污染指数序列进行三层小波分解,对各层高低频系数使用wrcoef函数进行单支重构,得到原始序列的小波分解序列{a3,d3,d2,d1},其中a3为低频子序列,是原始序列的近似,反映了原始序列的长期变化趋势;d3,d2,d1是高频子序列,是原始序列的细节,反映了原始序列在不同“焦距”下的随机性和波动性。小波分解的结果如图1所示:
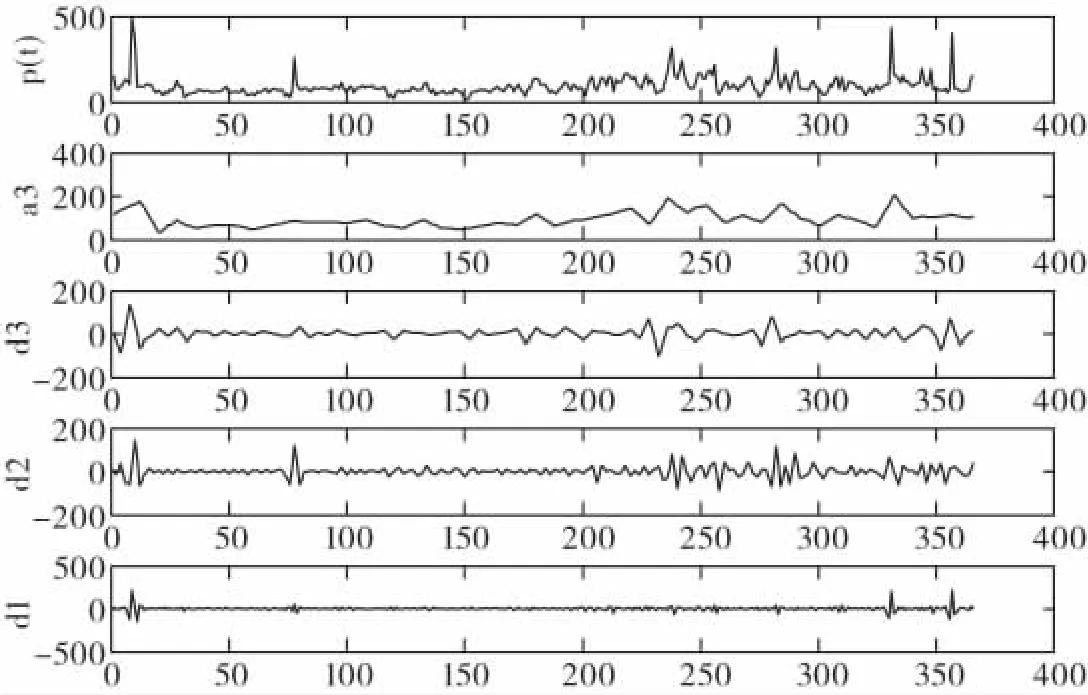
图1 原始时间序列的小波分解
2.2.2 网络结构
小波神经网络综合了小波变换的分辨率性质和神经网络的自学习能力,在处理非线性问题时表现优异,已广泛用于各个领域[6-7]。
小波神经网络主要有两种结构:松散型和紧凑型。松散型不改变网络的结构,首先利用小波对信号进行多层分解,然后将分解得到的小波系数序列交由神经网络处理,特别适用于非平稳信号的预测与分析。紧凑型结构则以小波基函数作为隐层单元的激励函数,常用的小波基函数为Morlet函数,本研究采用松散型结构,网络分为输入层、隐层和输出层。
取2011.4.21 日 -2012.4.20 日气象数据中的最高温度、最低温度、平均风速、相对湿度、前一日空气污染指数及小波单支重构序列{a3,d3,d2,d1}作为网络的最终输入,共9个输入,输出为空气污染指数。网络结构如图2所示:
3 网络训练和仿真
以2011.4.21-2012.4.20 的数据作为训练样本,将数据按维度归一化至[-1,1]。隐层单元范围由经验公式确定[15],假设n1,n2分别为输入层和输出层单元数,n为隐层单元数,则最佳隐层单元的范围为:[log2n1,+[1,10]],在此范围内经过多次实验,比较训练误差和测试误差,最终取n=13。因此,网络结构为9-13-1。隐层和输出层转移函数分别为tan-sig、purelin,采用 traingdx 算法训练网络,训练精度0.001,lr=0.015。

图2 小波神经网络结构图
将2012.4.21日-2012.6.17日的58个样本作为测试样本,使用WNN模型进行测试,当训练步数达到2303步时网络收敛,其误差平方曲线如图3所示。
仅以四个气象因子和前一日的空气污染指数作为BP网络输入对相同的样本进行测试,两种模型的测试结果如表1所示。
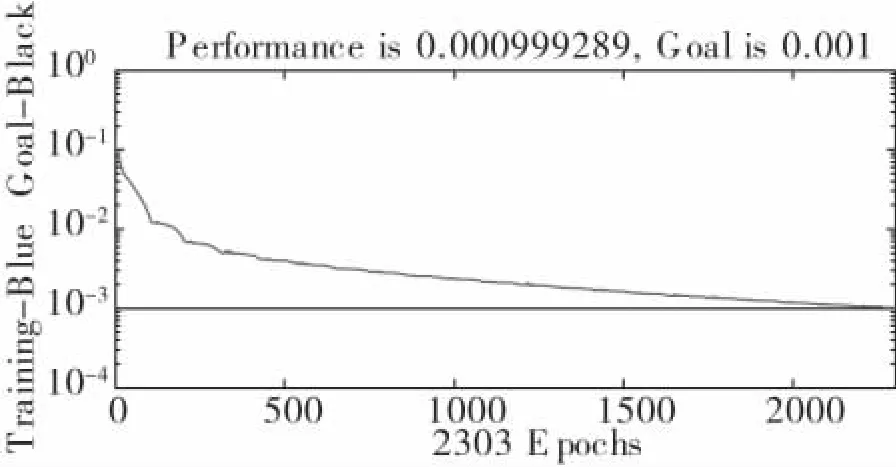
图3 误差平方曲线

表1 小波神经网络和BP网络仿真结果对比
从仿真实验的结果可知,两种模型都能反映出空气污染指数序列的总体变化趋势。从收敛速度来看,BP网络在训练精度为0.01时,到达预设的10000步才收敛,收敛速度慢。比较两者的预测精度,BP神经网络在时间序列的平稳阶段预测精度较好,但在时间序列波动较大的阶段,预测精度较差,部分原因在于训练样本较少导致欠学习,模型泛化能力不高,更重要的原因在于有限样本中包含的信息量少,输入中没有时间序列本身的趋势性及波动性信息。小波神经网络由于对原始序列进行了小波分解,其低频序列能够表现空气污染指数序列的趋势性,各尺度上的高频子序列则反映了空气污染指数序列的随机性和波动性。这种多尺度分析能够以任意精度“聚焦”原始序列在任意细节上的差异性,有利于提前预判序列的变化趋势及局部的波动性,从而提高网络的预测精度,特别当时间序列局部波动性较大时,效果更为明显,充分显示了小波神经网络模型较强的鲁棒性。表1对比了两种模型的收敛速度及预测精度,其中MAE为平均绝对误差。
从表1可以看出,与BP神经网络相比,小波神经网络具有更好的预测精度,更快的收敛速度以及较好的自适应性。
4 结语
BP神经网络预测空气污染指数时收敛速度慢、泛化能力较差,提出了小波神经网络预测模型,研究了网络模型的结构及参数对网络性能的影响。对空气污染指数的仿真结果表明该模型对序列的平稳和非平稳阶段均具有较高的预测精度和鲁棒性,是一种行之有效的空气污染指数预报方法。基于各种智能算法自适应调节权重参数和学习率,进一步提高小波神经网络的预测精度、收敛速度及泛化能力将是下一步的研究方向。
[1] 王海鹏,等.基于小波变换的兰州市近十年空气污染指数变化[J].环境科学学报,2011,31(5):1071-1076.
[2] 张静,李旭祥,许先意,等.大气环境数据分析预测方法对比研究[J].中国环境监测,2010,26(6):66-70.
[3] 王芳,程水源,李明君,等.遗传算法优化神经网络用于大气污染预报[J].北京工业大学学报,2009,35(9):1230-1234.
[4] 高建华.兰州市大气污染规律及治理对策[J].西安石油学院学报:自然科学版,2003,18(4):85-88.
[5] 周秀杰,苏小红,袁美英.基于BP网络的空气污染指数预报研究[J].哈尔滨工业大学学报,2004,36(5):582-585.
[6] 张坤,郁湧,李彤.小波神经网络在黄金价格预测中的应用[J].计算机工程与应用,2010,46(27):224-241.
[7] 杨艳,李靖,马显莹,等.基于小波神经网络的城市用水量长期预测研究[J].云南农业大学学报,2010,25(2):272-276.
[8] 沈花玉,王兆霞,高成耀,等.BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008,24(5):13-15.

