基于希尔伯特-黄变换的双馈异步风力发电机定子故障诊断研究

陈继宁，马宏忠，时维俊，陈涛涛

（河海大学能源与电气学院，南京 210098）

风能作为一种可再生能源，正在受到越来越多的关注。风力发电机中双馈异步发电机(DFIM)占有很大的市场份额[1]。因此，为了确保电机的安全运行，进行及时的维护和提高运行的可靠性，以及最大化利用风能，电机的在线监测和早期故障诊断具有重要的意义。

与所有的电机一样，双馈风机易于发生电气机械故障，故障可能发生于定子、转子、轴承、气隙（偏心）等处。然而，资料表明，电机失效大多数是由轴承故障和定子绝缘击穿所引起的[2,3]。异步电机定子绕组绝缘劣化是引起电机失效的主要原因(约占40%)[4]。定子故障起始于匝间绝缘的劣化，进而发生匝间短路。因此，需要在匝间短路初期及时地检测出来，以免故障扩大造成崩溃或重大损伤。

当双馈风力发电机发生定子绕组匝间短路时，如果故障比较轻微，三相定子电流的变化非常微小，此时仅从时域波形无法识别出是否存在定子匝间短路故障[5]。传统的傅里叶变换是整个时间轴上的积分，因此不能给出时间域的信息，只适用于稳态信号的特征提取，对于变化中，或者刚发生故障的信号并不能有准确的判断[6]。小波变换(WT) 是 20 世纪 80 年代由法国地球物理学家J Morlet在分析地震波时提出的一种非平稳信号分析理论，近年来在信号分析方法上有重大突破，并已在故障诊断领域得到成功应用[7,8,9]。在分析频率逐渐变化的数据时，小波变换很有效，其结果具有解析形式。但小波变换主要基于傅里叶分析，不可避免具有傅里叶分析的局限性。对于正常频率与故障频率基本相同或变化微弱的信号，如早期匝间故障造成的信号的微小变化，小波变换则无法有效提取其故障特征[10]。

本文采用希尔伯特-黄变换(Hilbert-Huang Transform)[11]对双馈风力发电机定子绕组故障进行分析，即对在动模实验室采集到的电流信号进行变换，根据第4或者第5层固有模态函数(IMF)分量的瞬时幅值或瞬时频率可以确定出匝间短路故障及其出现和结束的时刻，便于定子匝间短路故障的实时监测、确定和及时维修。

1 希尔伯特-黄变换方法

希尔伯特-黄变换(HHT)是美国宇航局(NASA) 的Norden E Huang等人于1998提出的一种新的时间序列信号分析方法，这是在历史上首次对Fourier变换的基本信号和频率定义作的创造性改进，主要应用于非平稳信号，尤其是突变信号的分析。

HHT方法由 EMD和 Hilbert变换两部分组成，EMD分解用来提取经验模态函数(IMF)；然后对 IMF进行Hilbert变换可获得瞬时频率和瞬时振幅，二者皆为时间的函数。根据瞬时频率或瞬时幅值可进行故障特征提取。下面将HHT应用于电机故障诊断。

1.1 EMD方法对 i（t）进行分解

电机电流信号均包含有多种振荡模态，直接对其进行Hilbert变换得到的瞬时幅值是毫无意义的。EMD基于信号的局部特征时间尺度，可以将任意复杂的信号分解为少量 IMF的组合， IMF表征了内蕴于数据的振荡模态[12]给出合理的瞬时幅值，IMF分量必须满足下面两个条件：一是在整个数据长度上，信号极值点的数量与过零点的数量相同或者至多相差 1个；二是在任意点，由局部极大值点构成的包络线和局部极小值点构成的包络线的平均值为零。这样一个信号可以表示为若干个IMF和一个残差的和，如下式所示

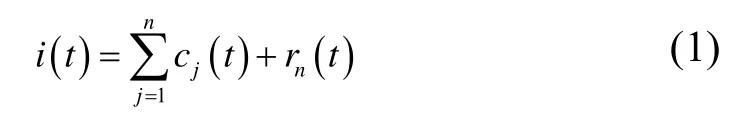
其中mj(t)是第j个模态函数，rn(t)是残差。

为了提取信号i（t）的模态函数，步骤如下：

（1）将原始信号i（t）上所有的极大值点用三次样条函数拟合成数据的上包络线，所有的极小值点拟合成下包络线，上下包络线的均值，记为m1(t)；

（2）将原始信号i（t）减去该均值即可得到一个去掉低频的新数据序列h1(t)；

（3）h1(t)一般仍不是一个 IMF分量序列，为此需要对它重复进行上述处理过程，直到h1(t)符合 IMF的定义要求，这样就得到了第1个IMF分量c1(t)，它代表信号i（t）中最高频率的分量；

（4）将c1(t)从i（t）中分离出来，即得到一个去掉高频分量的差值信号r1（t），即有

将r1（t） 作为原始数据，重复步骤（1）、（2）和（3），得到第二个IMF分量c2（t），本文重复6次 ,得到6个IMF分量。

1.2 IMF的希尔伯特变换

电流信号i（t）的Hilbert变换H(t)为

其反变换为

则与之形成复共轭时，由其构成的解析信号为

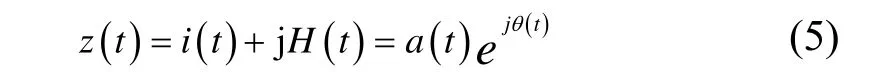
式中:a（t）为瞬时振幅，θ(t)为相位。

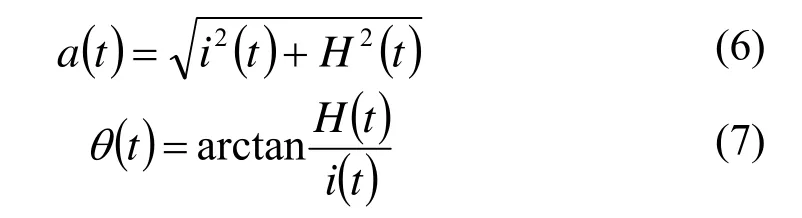
2 实验测试与研究

采用了如图1的系统结构图来测试不同负载下的双馈风机定子电流。直流电动机与双馈异步发电机（用YZR160M-4绕线异步电机代）之间用机械连接，直流电动机的转速模拟风速，带动绕线式异步电机转动。定子侧通过升压变压器与电网相连；转子侧有励磁系统，转子绕组通过变频器实现对风力发电系统的变速恒频控制。

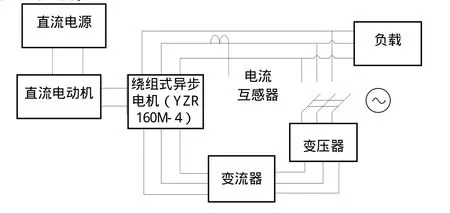
图1 双馈风机定子绕组匝间短路故障实验原理图

YZR160M-4电机主要参数如下：定子额定电压：380V，定子额定电流：12.5A，转子额定电压：184V，转子额定电流：20A，电机额定功率：5.5kW，4极。直流电动机型号为Z2-51，额定功率：5.5kW，额定电压：220V，额定电流：30.9A，额定转速：1500r/min。电流互感器型号为ML-6.0。数据采集装置选用尼高采集仪，型号为Nicolet7700。

发电机的定子绕组在设计阶段就已经安装好抽头，通过抽头的连接实现定子绕组内部一匝短接，来模拟匝间短路初期故障。考虑到匝间短路对电机寿命的影响，故抽头短接时间越短越好，最大不超过1秒。

系统分别在空载、半载以及额定负载情况下，进行了定子绕组一匝短路故障试验。采集到的三相定子电流实测波形图如图2所示，可以看出故障发生时，三相定子电流的变化非常微小，仅从时域波形很难识别出是否存在定子匝间短路。下面以额定负载情况为例进行说明：对发电机定子三相电流进行FFT分析（图3），可以看出故障情况下与正常状态差别不大。在对发生瞬态匝间短路的定子电流信号进行小波分析时，同时对小波基 db1 、db2 、db3 、db5 、sym1 、sym2 、sym3 、sym5 、coif1 、coif3 、coif5 都进行了尝试，没有发现故障特征。图4以db2小波为例，可以发现短路发生时，并没有引起小波分解信号的突变。

图2 双馈风机在空载（上）、半载（中）和额定负载（下）下定子匝间短路时定子电流波形图

图 5(a)～5(b)为实验测得的双馈电机在空载情况下的电流信号的 6层经验模态函数 IMF图及其 Hilbert变换后的瞬时幅值图，图 6(a)～6(b)为半载情况下的IMF图以及其Hilbert变换后的瞬时幅值图，图7(a)～7(b)为额定负载情况下的IMF图以及其Hilbert变换后的瞬时幅值图。

由图5、图6和图7可以看出，HHT 得到的第4或者第5层IMF分量的瞬时幅值在故障产生和切除的时刻均有很大的突变，可以表征故障，获取故障产生和切除的时刻。这是因为，HHT根据信号包络分解出高频分量，由于三相短路故障中故障造成的幅值变化会引起信号包络的改变，使信号包络包含故障信息。如图5，6和7所示，第4或者第5层IMF的瞬时幅值所具有的故障特征正是这一故障信息的表现。因此，在造成信号包络变化但频率基本不变或变化微弱的故障情况下，传统的傅里叶变换以及小波变换均无法判断，此时HHT显示了它的优势和判断的及时性和准确性。

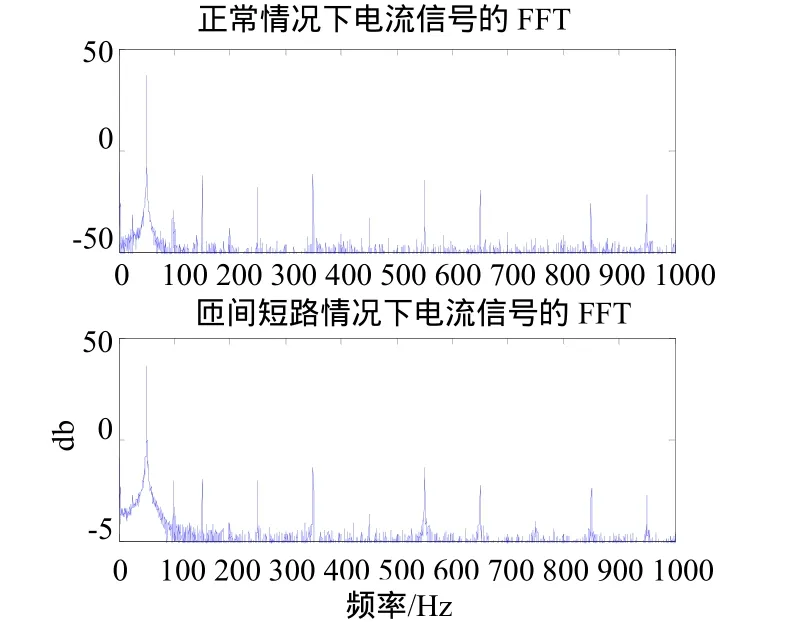
图3 双馈风机在额定负载时正常和匝间短路情况下的定子电流信号的频谱图

图4 双馈风机额定负载情况下定子匝间短路时定子电流信号的小波分解

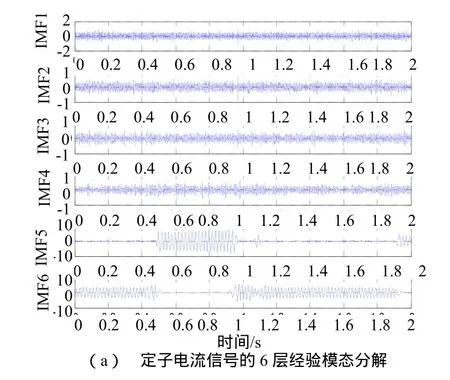
图5 双馈风机空载情况下定子匝间短路时定子电流信号的希尔伯特-黄变换

由双馈风机在空载、半载以及额定负载下定子电流希尔伯特-黄变换的瞬时幅值图可以看出，在故障初期即匝间短路发生的瞬间，瞬时幅值发生突变，因此可以判断出故障的发生。但是希尔伯特-黄变换只能判断出故障的发生，并不能在已经发生故障时估计故障的严重程度，也不能对故障位置进行准确定位，需要结合其他方法进行故障监测与诊断。

图6 双馈风机半载情况下定子匝间短路时定子电流信号的希尔伯特-黄变换

3 结论

本文通过实测数据对双馈异步风力发电机定子绕组故障进行研究，通过比较传统的FFT分析、小波分析以及HHT分析，指出第4或者第5层IMF瞬时幅值分析的优越性。分别对双馈发电机在空载、半载以及额定负载运行时的定子绕组匝间短路进行实验分析，得到如下结论：（1）在匝间短路故障比较微弱的时候，三相电流的变化非常微小，此时仅从时域波形无法识别出匝间短路的发生；（2）在匝间故障发生时，信号的频率几乎不发生变化，此时仅有信号幅值的变化，小波变换无法有效提取其故障特征；（3）对电流信号进行希尔伯特-黄变换，得出6层IMF的瞬时幅值图，可以看出，当匝间短路发生时，无论是空载、半载和额定负载，信号的第4或者第5层IMF的瞬时幅值均发生突变，可以判断匝间短路故障的发生，为匝间短路的及时发现与维修提供了一个有效的手段。

图7 双馈风机额定负载情况下定子匝间短路时定子电流信号的希尔伯特-黄变换

[1]Popa L M, Jensen B B, Ritchie E, et al. Condition monitoring of wind generators[C]//Industry Applications Conference, 2003. 38th IAS AnnualMeeting. Conference Record of the. IEEE, 2003, 3:1839-1846.

[2]Vas P. Parameter Estimation, Condition Monitoring,and Diagnosis of Electrical Machines (Monographs in Electrical and Electronic Engineering)[M].London, UK: Oxford Univ. Press, 1993.

[3]Nandi S, Toliyat H A. Condition monitoring and fault diagnosis of electrical machines-a review[C]//Industry Applications Conference, 1999.Thirty-Fourth IAS Annual Meeting. Conference Record of the 1999 IEEE. IEEE, 1999, 1: 197-204.

[4]Thomson W T, Fenger M. Current signature analysis to detect induction motor faults[J]. Industry Applications Magazine, IEEE, 2001, 7(4): 26-34.

[5]魏书荣, 符杨, 马宏忠. 双馈风力发电机定子绕组匝间短路诊断与实验研究[J]. 电力系统保护与控制, 2010, 38(11): 25-28.

[6]Gritli Y, Stefani A, Filippetti F, et al. Stator fault analysis based on wavelet technique for wind turbines equipped with DFIG[C]//Clean Electrical Power, 2009 International Conference on. IEEE,2009: 485-491.

[7]Zhang Z, Ren Z, Huang W. A novel detection method of motor broken rotor bars based on wavelet ridge[J]. Energy Conversion, IEEE Transactions on,2003, 18(3): 417-423.

[8]Douglas H, Pillay P, Ziarani A K. A new algorithm for transient motor current signature analysis using wavelets[J]. Industry Applications, IEEE Transactions on, 2004, 40(5): 1361-1368.

[9]宋志明, 霍永红等. 基于小波变换的HVDC 输电系统故障诊断研究[J]. 电力系统保护与控制,2012, 40(3): 100-104.

[10]杨露, 沈怀荣, 希尔伯特-黄变换与小波变换在故障特征提取中的对比研究[J]. 兵工学报, 2009,30(5): 628-632.

[11]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,1998, 454(1971): 903-995.

[12]刘毅华, 赵光宙, 希尔伯特-黄变换在电力系统故障检测中的应用研究[J]. 继电器, 2006, 34(14):4-6.