基于蒙特卡罗的CTCS-3级列控系统单元重要度分析

车玉龙,苏宏升

(兰州交通大学自动化与电气工程学院,兰州 730070)

高速列车运行的安全性直接关系到广大乘客的生命安全，一旦发生事故，后果非常严重。为保证行车安全，高速铁路必须采用列控系统[1]，列控系统的可靠性分析是保障列车安全运行的基础，因此研究列控系统的可靠性就显得非常重要。国内一些学者对CTCS-3级列控系统的可靠性[2-3]与安全性[4]进行了分析与评估研究。但是目前对组成CTCS-3级列控系统组成单元的重要度研究较少，而单元的重要度是系统可靠性分析的重要内容。

故障树分析(Fault Tree Analysis，FTA)是用于大型复杂系统可靠性和安全性分析的一个有力工具，FTA反映了单元失效、人为失误或子系统等事件引起顶事件发生的逻辑关系。近年来使用FTA方法研究铁路系统[5]及高速铁路列控系统的安全风险[6]取得了较好的效果。若故障树太复杂，尤其底事件不服从指数分布时，则会遇到计算量相当大的问题。蒙特卡罗方法简单、高效，其基本思想是通过计算样本均值来估计总体均值，用蒙特卡罗仿真求解故障树，对底事件所服从的分布类型没有限制，在很多领域得到了广泛应用[7-9]。

由实际经验知，系统中的单元并非同等重要的，如有的单元一旦失效就会引起系统失效，有的则不然。本文在深入分析CTCS-3级列控系统结构和功能的基础上，从系统失效的角度建立CTCS-3级列控系统失效的故障树模型，采用蒙特卡罗方法仿真故障树，计算CTCS-3级列控系统组成单元的概率重要度和结构重要度，从而识别列控系统的薄弱环节，为提高列控系统的可靠性和日常维护提供科学依据。

1 故障树分析方法

FTA是1961年由美国贝尔实验室的H.A.Wastson和D.F.Haasl首先提出的，采用逻辑框图(即故障树)形象地对可能造成系统的故障因素(包括硬件、软件、环境和人为因素等)进行分析，特点是思路清晰，逻辑性强，直观明了，既能定性分析，又能定量分析。通常进行FTA的程序是：选择顶事件，建立故障树，以及定性或定量地评定故障树。

在一个故障树中往往包含有很多的基本事件，这些事件并非是同等重要的，一般认为，一个基本事件或最小割集对顶事件发生的贡献称为重要度。一个单元重要度的衡定与该单元在系统整个生命周期不同阶段有不同的意义，在系统设计阶段，单元重要度的衡量可以用来识别薄弱点，用来提高整个系统的可靠性；在系统工作阶段，单元重要度的衡量可以用来合理分配维修和检查资源以保证更重要的单元。工程上常用的有概率重要度和结构重要度。

1.1 结构重要度

结构重要度是基本事件在故障树所在的位置对故障树整体的影响程度。即在假定各基本事件的发生概率都相等，或者说不考虑基本事件自身的发生概率的前提下，分析各基本事件的发生对顶事件发生所产生的影响。

设j是系统中任一单元，系统的结构函数为φ，若φ(0j,x)=0,φ(1j,x)=1，则表示j是一个关键部件，表明j正常时系统就正常，j失效时系统也失效。称(1j,x)为j的一个关键路向量。对于j单元某一给定状态，其余(n-1)个单元的可能状态组合共有2n-1种不同的结果，定义

nφ(j)=∑{φ(1j,x)-φ(0j,x)}

nφ(j)是第j个单元对系统失效贡献大小的量度。定义单元的结构重要度为

Iφ(j)=12n-1nφ(j)

它表明j的关键路向量数目在所有2n-1中可能情形中占的比例。因此，对任意的结构φ，单元可按其结构重要度排序。

1.2 概率重要度

结构重要度仅仅反映的是基本事件在故障树中所占位置的重要程度，而设备在系统中的重要性不仅依赖于其结构，还依赖于设备本身发生故障的概率。设备的概率重要度是指某设备故障发生概率的单位变化量所引起的系统故障发生概率的变化值，也即设备故障发生概率对该系统故障发生概率的变化率，称

Ih(j)=∂h(p)∂pj,j=1,…,n

为设备j的概率重要度。

2 蒙特卡罗方法

蒙特卡罗方法的基本思想是通过计算样本均值来估计总体均值，其理论基础是概率统计，基本手段是随机抽样，通过有关随机变量的统计抽样检验或随机模拟，从而估计和描述函数的统计量、求解问题近似解的一种数值计算方法，处理实际问题的基本步骤是：建立随机模型，定义随机变量，过程模拟，统计计算。

2.1 随机数

从蒙特卡罗方法的基本思想可以看出，对给定的分布进行抽样，得到一个随机数样本的过程在蒙特卡罗方法中占有非常重要的地位。随机数的产生可以分为均匀分布随机数的产生和非均匀随机数的产生2个方面，每一方面又有多种产生方法。

通过反函数法产生任意分布随机数是最常用的方法之一。将累积分布函数F(x)进行反变换，得到所需的反函数G(F(x))，通过G(F(x))就得到F(x)的随机数。显然累积分布函数F(x)取值范围为0～1，因为F(x)的定义为F(x)=P(X≤x)，为了生成一个概率分布的随机抽样，将生成一个在0～1之间的随机数(r)。然后将这个值带入到G(r)=x中得到符合分布F(x)的随机数。

2.2 基于蒙特卡罗的故障树模拟过程

用蒙特卡罗方法对故障树进行仿真具体有2种方法：基于最小割集的故障树仿真和基于结构函数的故障树仿真。基于最小割集的故障树仿真是对故障树的所有最小割集进行故障时间抽样，把这些最小割集故障时间的最小值作为系统失效故障时间的一个抽样值，记录此故障时间。重复此过程，最后通过对记录样本的统计分析，得到各个可靠性结果。后者是根据故障树的结构函数，通过抽样故障树的基本元件，对其失效时间进行排序，再依次检查各个底事件失效是否会引起顶事件发生，从而找出顶事件发生时间[8]。本文使用基于最小割集的故障树仿真，因为这种仿真方法能够准确定位系统中某单元的失效是否导致系统失效，且仿真过程中不用通扫整个故障树，也不用求取系统故障树的结构函数，相比之下仿真流程较简单，可以节省仿真时间。

2.3 计算重要度

(1)单元的结构重要度

Iφ(j)=P(j)N

其中，P(j)表示基本单元失效引起系统失效的次数；N表示基本单元失效总次数。

结构重要度表示了设备失效而引起系统失效次数在系统总失效中的百分比，因此Iφ(j)越大，说明越是系统可靠性薄弱环节。

(2)单元的概率重要度

Ih(j)=H(j)N

其中，H(j)表示基本单元失效引起系统失效的次数；N表示基本单元失效总次数。

概率重要度表示单元在系统中的重要程度，若Ih(j)=1，则说明只要设备j发生一次故障，则系统必定因其发生失效，为了提高系统可靠度，首先应该着眼于概率重要度较大的设备。

3 算例

3.1 CTCS-3级列控系统介绍

CTCS-3级列控系统是基于GSM-R无线通信实现车、地信息双向传输，无线闭塞中心(RBC)生成行车许可，轨道电路实现动车组占用检查，应答器实现列车定位，满足动车组运营速度350 km/h和最小追踪间隔3 min的要求，同时具备CTCS-2级列控系统功能的列车运行控制系统[10]。

CTCS-3级列控系统的结构如图1所示，包括地面子系统和车载子系统，车载子系统包括安全计算机(VC)、轨道电路信息接收单元(TCR)、应答器传输模块(BTM)及应答器天线、无线传输模块(RTM)、人机界面(DMI)、动车组接口单元(TIU)、测速测距单元(SDU)、司法记录器(JRU)等单元，地面子系统由无线闭塞中心(RBC)、列控中心(TCC)、轨道电路、应答器系统(含轨旁电子单元LEU)和临时限速服务器(TSR)构成。

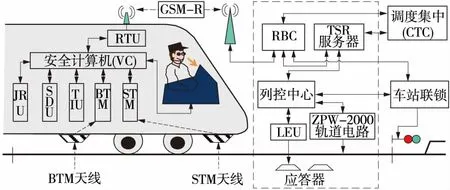
图1 CTCS-3级列控系统结构示意

3.2 故障树建立

CTCS-3级列控系统属于可维修系统，在分析之前先做以下假设：(1)各单元的寿命分布均服从指数分布；(2)每次故障的事件是独立事件，与其他事件无关；(3)不考虑共因失效；(4)系统中涉及到的比较器、表决器和司法记录器(JRU)等是完全可靠的，即故障率λ为0。

本文从CTCS-3级列控系统安全功能失效的角度出发，建立CTCS-3级列控系统的功能结构故障树，按照建立故障树的基本步骤，首先选择CTCS-3级列控系统失效为顶事件，根据各事件的功能逻辑关系由上到下建立故障树，如图2所示。

图2 CTCS-3级列控系统失效的FTA图

3.3 仿真结果

车载子系统的故障率数据来源于文献[2]，列控中心、轨道电路和应答器的故障率参数来源于文献[11]，RBC的故障率来源于ETCS(欧洲列车运行控制系统)中RBC的参数[12]。

蒙特卡罗仿真参数设置：有效失效时间下限为0，有效时间上限为1 000，随机数种子为100，分别模拟2 000次，4 000次，8 000次和10 000次。CTCS-3级系统设备(底事件)的结构重要度和概率重要度仿真计算结果如表1所示。

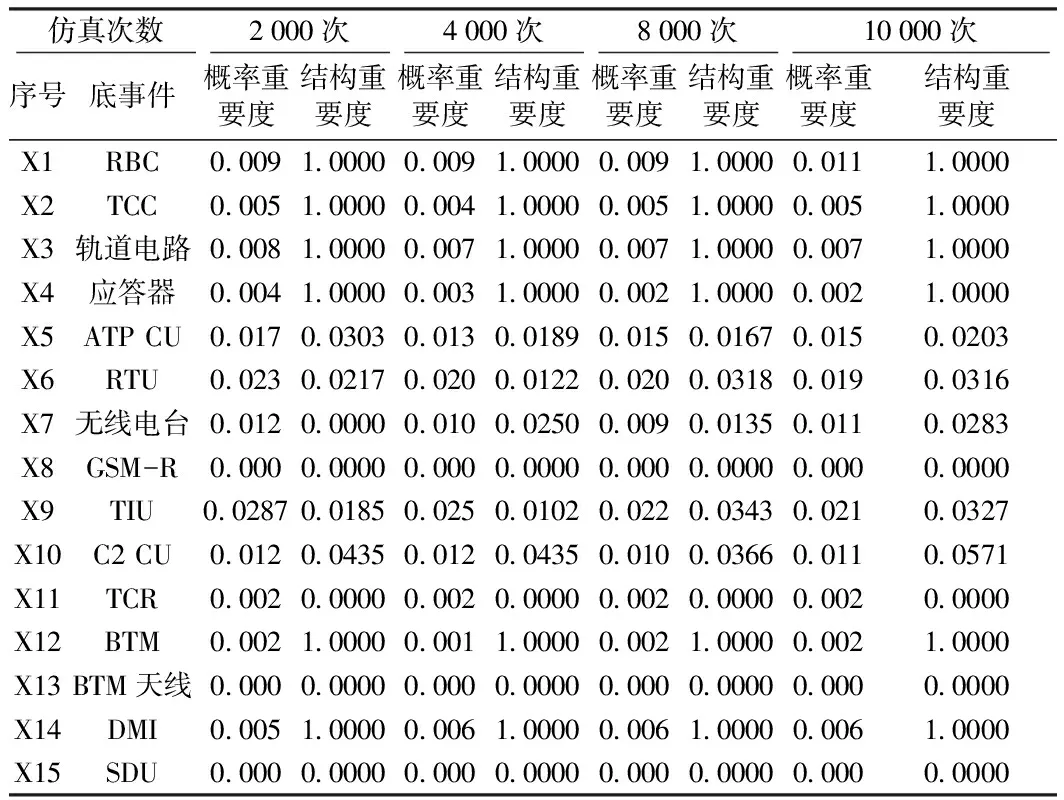
表1 CTCS-3级列控系统设备的重要度

从表1中可以看出，随着仿真次数的增大，仿真结果趋于稳定。从仿真10000次的结果可以看出，概率重要度排序是：TIU>RTU>ATP CU>RBC=C2 CU=无线电台>轨道电路>DMI> TCC>BTM=TCR=应答器>SDU=BTM天线=GSM-R；结构重要度排序是：RBC=TCC=轨道电路=DMI=BTM=应答器> C2 CU> TIU > RTU >无线电台> ATP CU>TCR=SDU=BTM天线=GSM-R。

为了提高列控系统的可靠性，应该着眼于概率重要度较大的设备，例如列车接口模块(TIU)的概率重要度大于GSM-R。从结构重要度的排序结果可以看出，列控系统地面设备较车载设备而言，列控中心(TCC)、轨道电路、应答器、人机界面(DMI)和应答器信息接受模块(BTM)等是列控系统可靠性的薄弱环节。

4 结语

在深入分析CTCS-3级列控系统结构和功能的基础上，从系统失效的角度建立CTCS-3级列控系统失效的故障树，采用蒙特卡罗方法对故障树进行仿真计算，得到列控系统组成单元的概率重要度和结构重要度，为提高列控系统设备的日常维护和管理者的科学决策提供依据。

[1] 张曙光.CTCS-3列控系统总体技术方案[M].北京：中国铁道出版社，2008．

[2] 邸丽清，袁湘鄂，王永年.CTCS-3级列控系统RAM指标评价方法研究[J].中国铁道科学，2010，31(6):92-97．

[3] 吴书学.CTCS3-300T列控车载系统运行可靠性分析[J]. 铁路通信信号工程技术，2012，9(1):8-11．

[4] 石先明，张敏慧.高速铁路列控系统安全性分析与改进[J].铁道标准设计，2012(11):101-106．

[5] 刘敬辉，戴贤春，郭湛，等.铁路系统基于风险的定量安全评估方法[J].中国铁道科学，2009，30(5):123-128．

[6] 张苑，刘朝英，李启翮，等.无线闭塞中心系统安全风险分析及对策[J].中国铁道科学,2010，31(4):112-117.

[7] 库明阳，郭建英.基于故障树的系统可靠性仿真分析[J].计算机仿真，2007，24(8):78-80．

[8] 马小玲.基于蒙特卡罗的故障树模型的仿真研究[J].电子设计工程，2011，19(3):128-130．

[9] 康健，周振华.基于费用最小的列控设备维修优化与仿真[J].铁道标准设计，2012(12):92-95．

[10] 铁道部.科技运[2008] 127号 CTCS-3级列控系统需求规范(SRS) (V1.0) [S].北京：中国铁道出版社，2008.

[11] 李清.CTCS-2级列控系统安全可靠性分析及运用研究[D].成都:西南交通大学，2010．

[12] UNISIG SUBSET 088， ETCS Application Levels 1 & 2 — Safety Analysis， Version 2.3.0， http://www.era.europa.eu/Document-Register/Pages/UNISIGSUBSET-088.aspx.