地铁区间施工周边环境安全风险评估方法研究

王 帆， 覃亚伟

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

地铁建设由于下穿城市腹地，容易造成周边环境如邻近建筑物、管线和路面破坏，因此需要在地铁施工过程中对周边环境进行风险评估，避免地铁施工危及周边环境的安全，造成不必要的人员伤亡和财产损失。

国际工程保险协会的报告指出大部分地下工程事故都发生在隧道施工阶段[1]，对地铁施工产生的周边环境风险进行风险评估时需要充分考虑地铁施工的特点，一方面，建立的地铁施工风险评估模型需要识别出所有相关的风险影响因素，确定风险影响因素之间及风险事件的关系，从而定性和定量地描述风险发生的场景、概率和后果[2,3]；另一方面，地铁施工中会产生大量历史数据，同时也需要依据专家的相关经验知识进行地铁施工安全风险分析，因此如何结合客观历史数据和主观专家判断是建立有效风险评估模型的关键。本文尝试建立地铁施工周边环境安全风险的定量评估模型，结合武汉地铁二号线的工程背景和实际需要，对地铁施工周边环境安全性进行分析，对施工风险管理具有一定的参考价值和指导作用。

1 周边环境风险影响因素

城市中地铁隧道施工对周边环境可能造成的破坏形式主要包括：(1)周边建筑物开裂、倾斜或垮塌；(2)路面开裂或塌陷；(3)周边地下管线的开裂[4]。因此，地铁隧道施工中需要对周边建筑物、周围路面及周边管线进行监测，依据相关的监测数据和周边建筑物、管线的属性进行安全评估，为采取适当的预防措施或补救措施提供决策支持。

黄宏伟[4]、骆建军[5,6]等人曾归纳了地铁施工过程中周边建筑物、管线和路面安全评估的内容和方法，并总结了分析所需要调查的建筑物、管线及路面的风险影响因素。例如，建筑物破坏模式十分复杂，不同的结构形式、破坏原因造成的破坏形式差异较大，应综合考虑建筑物上部结构和下部结构的相关参数及监测结果进行分析，如裂缝(长度、宽度、位置、数量)、建筑物结构形式反映了建筑物上部结构的刚度，即抵抗不均匀沉降的能力，倾斜度反映了不均匀沉降的大小，而基础埋深、基础类型等参数则决定了建筑物下部结构受地铁施工影响的程度。此外，建筑物与地铁的相对位置关系也是影响建筑物安全状况的影响因素之一，通常建筑物距离地铁越远，受影响程度越小，反之则影响越大。可见，对建筑物进行风险评估需要综合监测结果和建筑物相关资料数据进行判断，本文采用建筑物基础类型、基础埋深、结构形式、建筑物高度、建筑物与地铁水平距离、建筑物距开挖面水平距离、已用年限、裂缝和倾斜度等作为影响建筑物安全状况的因素。同样，本文对地铁盾构施工过程中对路面和管线的风险影响进行了类似分析。由于风险影响因素较多，风险影响因素与风险事件之间的影响关系较为复杂，目前在分析方法上仍然以定性分析为主，缺少相应的定量分析模型。

本文基于故障树、事件树分析，模糊理论，相关向量分类机和贝叶斯网络构建了地铁施工周边环境风险评估模型，定量描述了风险影响因素与风险的因果关系以及风险传播的影响大小，为地铁施工风险管理提供决策依据。

2 混合概率风险评估模型

常用的风险评估方法包括事件树/故障树分析、模糊逻辑、机器学习和贝叶斯网络等方法。

故障树分析是一种演绎法，从顶事件开始进行演绎分析，依据分析的深度找出所有基本事件或因素，不同基本事件或因素的相互关系通过逻辑关系如“与门”、“或门”进行表示，并能够基于基本事件发生概率和逻辑关系计算顶事件的发生概率；而事件树分析是一种归纳法，从初始事件开始找出所有可能的后续事件，这些后续事件通常为阻止初始事件发展为事故的安全措施的状态，通过事件序列描述了事故场景。如果能够获得初始事件和后续事件发生的概率，则可以基于每个事故序列计算事故发生的大小。然而，基于事件树/故障树的风险分析方法需要大量统计数据来估计每个事件的发生概率，而地铁隧道施工往往缺少这些数据，相比之下，地铁隧道施工较为依赖于经验知识，因此常常需要专家判断作为客观数据的一种补充。

模糊逻辑方法在模糊集理论的基础上通过加入if-then模糊规则使得模型具备推理能力，从而可以表达专家知识并构建合适的专家系统，因此也常用于风险分析，如Zeng等人[7]基于模糊推理通过风险可能性，风险严重性和因素指数三个指标来衡量风险的大小并应用到高层建筑建设项目风险评估中。然而，模糊逻辑需要为每种输入变量状态的组合定义一个if-then规则，因此规则数会随着输入变量的数量或者变量状态的增加而呈指数增加，使得模型的构建非常复杂。

相比之下，机器学习方法可以通过对已有样本案例的学习模拟风险影响因素与对应风险之间的复杂关系，简化了建模的过程，常用的机器学习方法如神经网络和支持向量机等，如Wang和Elhag[8]采用人工神经网络分析既有桥梁的结构安全风险指数并以此确定维修的优先顺序。然而应用机器学习方法需要一定量的学习样本，而且通常无法给出风险分析结果的不确定性。

最近，使用贝叶斯网络进行风险分析受到极大关注，如Sousa和Einstein[9]基于贝叶斯网络分别建立了隧道施工开挖面前方地质状况的预测模型和在此基础上选择开挖方式的决策模型。贝叶斯网络主要有以下几个优点：(1)能够将客观数据和专家知识整合到一个模型中；(2)用图形的方式形象的表示出变量之间的因果关系；(3)有坚实的数学理论基础，用概率的方式定量的表达变量间因果关系影响的传播，从而对问题进行推理或诊断；(4)在获得新的信息(证据)后，可以计算变量的后验概率，从而对模型进行更新。然而目前大多数贝叶斯网络主要分析处理的是离散变量，而地铁盾构施工中如监测数据和隧道设计参数都是连续变量，并且需要结合专家判断进行分析，所以在进行贝叶斯网络建模时的一个主要问题就是如何充分利用既有的信息，在模型中结合历史客观数据等连续变量和专家主观判断等离散变量进行综合分析。

综上所述，考虑到地铁盾构区间施工的特点及安全风险分析的复杂性，本文通过结合上述风险分析方法的优点，构建了一个混合风险分析评估模型，基于历史客观数据和专家主观判断两类数据进行风险分析。

2.1 贝叶斯网络

贝叶斯网络，又称贝叶斯信度网络(BBN)，是由若干表示系统变量的节点和表示变量间因果关系的边组成的有向无环图(DAG)，如果边由节点X指向节点Y，则称X为Y的父节点，Y为X的子节点，其中没有父节点的节点为根节点，没有子节点的节点为叶节点，每个根节点联系有一个先验概率表(PPT)表示节点的先验概率，而每个非根节点联系有一个条件概率表(CPT)列出了此节点相对于其父节点所有可能的条件概率。贝叶斯网络的计算过程就是求所有节点的联合概率分布，由贝叶斯网络的条件独立性假设可知求网络中变量集U={X1,…,Xn}联合概率分布的链式规则：

(1)

其中，Parents(Xi)表示节点Xi的父节点集合，基于联合概率分布可以求得网络中任一变量的边际概率或条件概率。如图1所示的一个由4个节点组成的贝叶斯网络包含所有节点的联合概率分布为：

P(A,B,C,D)=P(D|B,C)P(B|A)P(C|A)P(A)

(2)

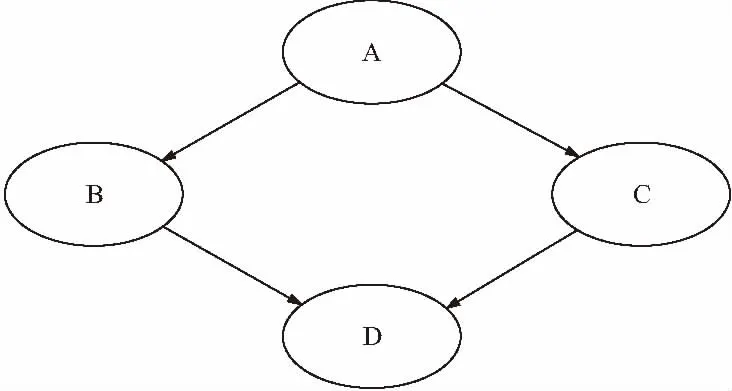
图1 贝叶斯网络示意

可以看出，贝叶斯网络是基于概率论和图论的一种不确定性知识表达和推理模型，它由两部分组成：网络结构构成了贝叶斯网络的定性部分，它表示变量之间的因果关系，是某一专业领域的一种知识表达；先验概率表和条件概率表给出了贝叶斯网络的定量部分，它表示变量间因果关系影响的强弱程度。贝叶斯网络建模实际上就是先对网络的定性部分建模，再对定量部分建模：

(1)建立贝叶斯网络结构

贝叶斯网络建模从建立有向无环图(DAG)开始，它代表了网络的定性部分，即网络结构。通常可依据相关专业知识背景进行确定。由于FTA/ETA在隧道及深基坑施工的风险分析中有着较好的识别事故因果关系和事故场景的能力，此外实际施工中往往要结合专家判断分析可能导致风险的因素及其因果关系，因此本文采用基于故障树/事件树转化为贝叶斯网络然后通过专家修改的方式构建网络结构。

(2)建立先验/条件概率表

贝叶斯网络节点的先验概率表(PPT)和条件概率表(CPT)给出了网络的定量部分，即网络节点间因果关系影响的强弱程度。通常可基于专家判断建立节点间影响程度的概率分布。

假设描述节点X对节点Y影响程度(如事件X发生导致事件Y发生的条件概率P(Y=1|X=1)的隶属度函数如图2所示，共有极低(VL)、低(L)、中等(M)、高(H)、极高(VH)五种描述，转化为模糊数形式如表1所示，以“中等”对应的模糊数为例，0.35和0.65分别为影响程度属于中等的下限值和上限值，而0.5为影响程度属于中等的最可能值。

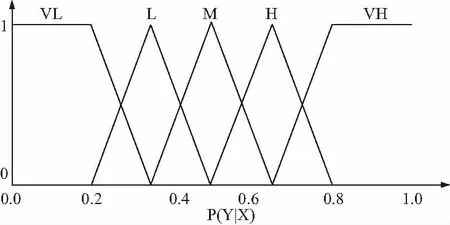
图2 节点影响程度的隶属度函数

语言描述模糊数极低fVL=(0, 0, 0.2, 0.35)低fL=(0.2, 0.35, 0.5)中等fM=(0.35, 0.5, 0.65)高fH=(0.5, 0.65, 0.8)极高fVH=(0.65, 0.8, 1, 1)

由于模糊数不利于贝叶斯网络计算，需要将模糊数转化为“脆值”。将模糊数转化为脆值有几种方法，如重心法、加权平均法[10]，但许多方法在转化过程中会损失部分信息，本文采用f加权估值函数[11]来减小这种信息损失：

(3)

其中，Val(F)为基于模糊隶属度函数F转化后的脆值，Fα={x|F(x) ≥α}是F的α截集，Average(Fα)是α截集元素的平均数，f(·)是f加权估值函数。对于常见的三角模糊数，隶属度函数形式如下：

F(x,(a,b,c)) =Triangular(x,(a,b,c))

(4)

设α截集元素的平均数Average(Fα)为：

(5)

其中，uα和vα分别为α截集上下界，uα=(b-a)×α+a，vα=c-(c-b)×α。

设f加权估值函数f(α)=1，则式(3)变为：

(6)

2.2 相关向量分类机

由于影响环境风险的风险影响因素很多，而对应的风险事件是受这些影响因素共同作用影响的，因此本文采用机器学习方法分析风险影响因素与风险事件的影响关系。但常规的机器学习方法如ANN，SVM无法给出分析结果的不确定性，使得基于这些方法估计的事件没有相应的概率分布，因而无法与贝叶斯网络进行整合。相关向量分类机(RVC)[12]作为一种新的分类方法，不仅可以给出分类的结果，还可以给出分类结果的不确定性(即概率)。

对于一个二分类问题，分类结果tn∈{0,1}，RVC使用常用的Sigmoid逻辑连接函数σ(y)=1/(1+e-y)作为y(x)的分类函数，则数据集的似然度式为：

(7)

由于这种形式权值w没有解析解，因此采用Laplace算法求其近似解。对于给定的一组超参数α，可以计算其相应权值的最可能值wMP，由于p(w|t,α)∝P(t|w)p(w|α)，因此求wMP等价于最大化下式：

(8)

Laplace算法简化为对logp(w|t,α)的二次逼近，则对式(8)进行两次微分：

(9)

B=diag(β1,…,βN)是对角矩阵，βn=σ{y(xn)}[1-σ{y(xn)}]。

∑=(ΦTBΦ+A)-1

(10)

wMP=∑ΦTBt

(11)

对于多分类问题，可以将其转化为多个二分类问题。为简便起见，本文采用二叉树方法先将所有类别分成两个子类，再将子类进一步划分成两个次级子类，如此循环，直到所有的节点都只包含一个单独的类别为止，该方法对于K分类问题只需要构建K-1个分类器，计算复杂度较小。

2.3 模型推理

在建立好混合模型的结构和变量间的影响关系后就可以基于观测到的风险影响因素进行风险评估。整个风险评估过程可以总结为四步(如图3所示)：

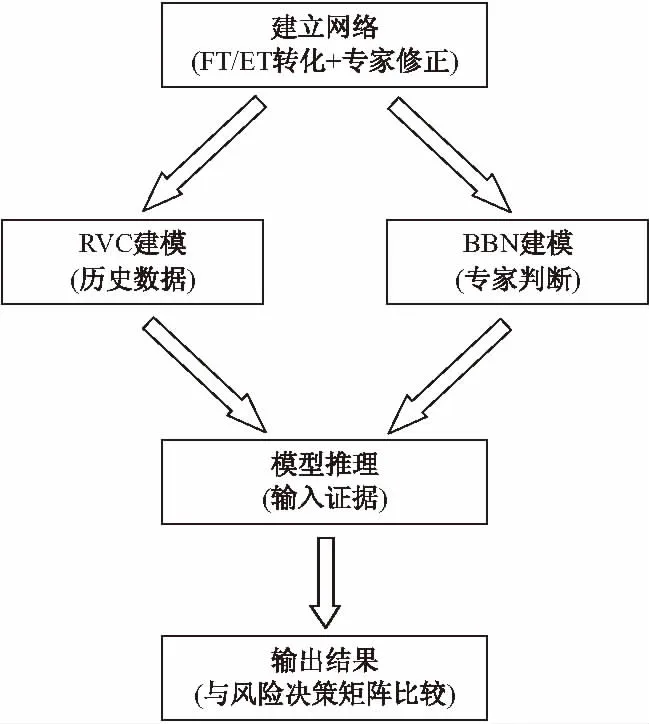
图3 基于混合模型的风险评估过程

(1)建立模型的网络结构。首先通过故障树/事件树分析得出风险类型、风险影响因素及相应的事故场景，再依据前文提到的方法将其转化为贝叶斯网络，在此基础上通过专家修正进一步完善网络结构。这一步是构建混合概率风险评估模型的定性部分；

(2)建立网络节点间的关系。第二步包含两方面，对于风险影响因素与触发事件间的关系，搜集相关的风险影响因素的数据样本，通过相关向量分类机进行建模，得到两者间的影响关系；对于网络中的其他部分，通过专家判断给出节点间的条件概率表通过贝叶斯网络建模；

(3)判断风险大小。在获取新的风险影响因素的观测值后，首先基于相关向量分类机进行分析，给出相应触发事件的概率分布，然后将其输入对应的贝叶斯网络根节点作为节点的先验概率表，基于贝叶斯网络进行推理，得到事故后果对应的概率分布。

(4)得出风险等级。最后将风险大小，即事故后果及对应的概率分布与风险接受准则(如ALARP准则)进行比较，确定风险等级，以便于管理者采取相应的措施。

3 案例分析

武汉市江汉路-积玉桥区间(简称江积区间)是武汉地铁2号线的越江段，该隧道为双洞隧道，采用泥水盾构施工方法，本文以江积区间江南岸上段(积玉桥—武昌风井)左线为例说明模型的分析结果。

经过分析得出的模型网络结构如图4所示。风险影响因素与建筑物破坏等级、路面病害等级和管线破坏等级的关系采用RVC建模，而贝叶斯网络建模所需的条件概率表可借鉴Eskesen 等人[13]在隧道建设风险管理指南中给出的事故频率分级标准(见表2)作为专家判断的参考依据，并依式(6)计算出所有节点的条件概率表。例如，专家判定当建筑物破坏等级为严重，且预防措施不到位时，发生建筑物垮塌的描述为“可能”，则专家意见所对应的三角模糊数为(0.03, 0.1, 0.3)，对应的条件概率为：

P(事故=垮塌|建筑物破坏等级=严重，

(12)

图4 地铁施工周边环境风险模型

频率等级概率区间中间值等级描述5>0.31非常可能40.03～0.30.1可能30.003～0.030.01偶尔20.0003～0.0030.001不可能1<0.00030.0001非常不可能

以建筑物为例，本文共收集了105条历史数据，每条数据样本包含建筑物安全风险影响因素的实际观测值以及对应的建筑物破坏等级，并用前80个数据样本作为训练集，其余25个作为测试集对RVC进行验证。预测结果精度为92%表明建立的相关向量分类机效果可靠。然后将所有的数据样本作为训练集建立建筑物破坏等级的3分类器，当获得新的建筑物安全风险影响因素的观测值时就能用来预测建筑物破坏等级。地面病害等级和管线破坏等级采用同样的方式获得，分类结果见表3。

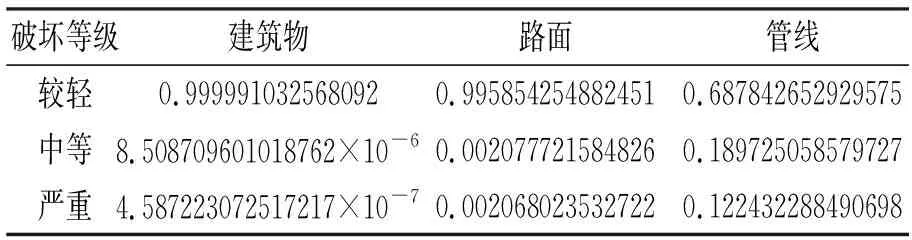
表3 破坏等级分类结果

可以看出，尽管三个节点都分为“较轻”这一类，但管线破坏等级分类的不确定性明显高于其他两者。接下来将概率分布输入到相应的贝叶斯网络节点进行贝叶斯网络推理，分析结果见图5。

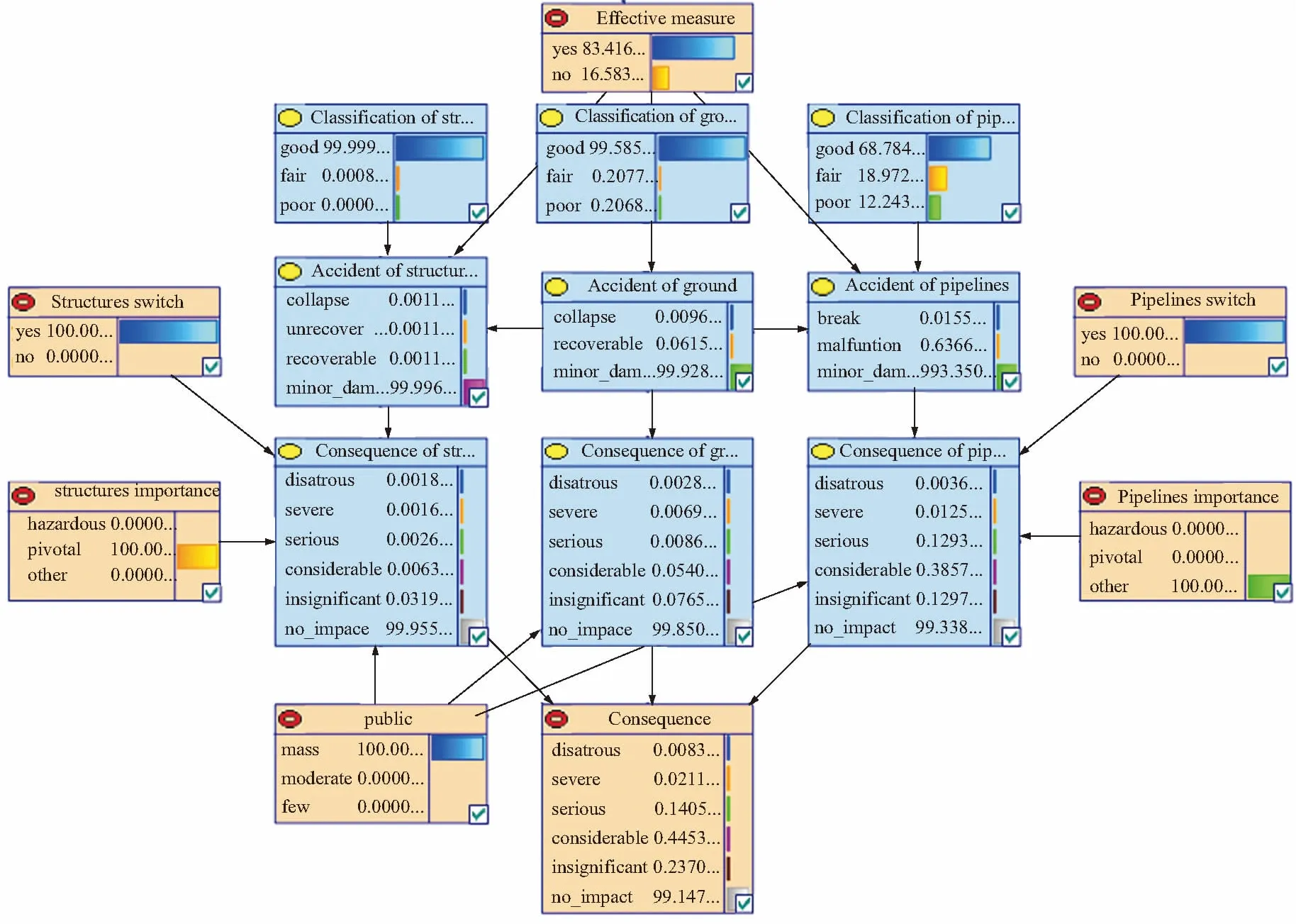
图5 贝叶斯网络风险分析结果

4 结 语

城市地铁施工通常规划在市区繁华地带，由于往往需下穿城市建筑群，施工条件及周边环境复杂，不确定性因素多，容易对周边环境造成较大影响，是一项高风险建设工程，因此需要在地铁工程的施工过程中对周边环境进行风险评估，从而采取相应的风险控制措施。本文提出了一个基于相关向量分类机和贝叶斯网络的概率风险评估方法，针对地铁施工特点结合历史数据和专家经验，通过专家知识表达和数据分析描述风险影响因素的风险传播路径和影响程度，对地铁施工过程中引起的周边建筑物、管线等环境安全风险进行风险分析，从而作为安全措施的指导依据。

[1] Cárdenas I C,Al-Jibouri S S H,Halman J I M,et al. Capturing and integrating knowledge for managing risks in tunnel works [J]. Risk Analysis, 2013, 33(1): 92-108.

[2] Øien K. Risk indicators as a tool for risk control [J]. Reliability Engineering and System Safety, 2001, 74(2): 129-145.

[3] Kaplan S, Garrick B J. On the quantitative definition of risk [J]. Risk Analysis, 1981, 1(1): 11-27.

[4] 黄宏伟，陈 龙，胡群芳，等. 隧道及地下工程的全寿命风险管理[M]. 北京: 科学出版社， 2010

[5] 骆建军，张顶立，王梦恕，等. 地铁施工对邻近建筑物安全风险管理[J]. 岩土力学，2007，28(7): 1477-1482.

[6] 骆建军，张顶立，王梦恕，等. 北京地铁暗挖车站施工对管线的影响分析[J]. 铁道学报，2007，29(5): 127-132.

[7] Zeng J,An M,Smith N J.Application of a fuzzy based decision making methodology to construction project risk assessment [J]. International Journal of Project Management, 2007, 25(6): 589-600.

[8] Elhag T M S, Wang Y. Risk assessment for bridge maintenance projects: Neural networks versus regression techniques [J]. Journal of Computing in Civil Engineering, ASCE, 2007, 21(6): 402-409.

[9] Sousa R L, Einstein H H. Risk analysis during tunnel construction using Bayesian Networks: Porto Metro case study [J]. Tunnelling and Underground Space Technology, 2012, 27(1): 86-100.

[10]Ross T J. Fuzzy Logic with Engineering Applications [M]. West Sussex, England:McGraw-Hill, Inc. 1995.

[11]Detynieckim M, Yager R. Ranking fuzzy numbers using alpha-weighted valuations [J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2000, 8(5): 573-592.

[12]Tipping M E.Sparse Bayesian learning and the relevance vector machine [J]. Journal of Machine Learning Research, 2001, 1(3): 211-244.

[13]Eskesen S D,Tengborg P,Kampmann J, et al. Guidelines for tunnelling risk management: International tunnelling association, working group No. 2 [J]. Tunnelling and Underground Space Technology, 2004, 19(3): 217-237.