基于模糊物元-综合集成赋权的工程评标模型

刘文娜， 舒 欢

(河海大学 商学院， 江苏 南京 210098)

在我国建筑工程交易中，施工项目实行招投标制度是建设管理体制改革的重点，也是市场经济发展的必然产物，而评标工作又是招投标过程中承上启下的一个重要环节，因此，评标方法原则与标准的制定是这一环节中具有决定性作用的关键因素，也是项目招标评标成功的基础。鉴于此，建立科学合理的评标方法不仅关乎项目的评选结果和投资效益，还影响着建设市场公平竞争环境的营造，对评标决策方法进行深入研究有着重要的现实意义。

从目前的招投标决策研究方法来看，大多是借助数学模型进行评标决策：AHP法、熵权系数法、模糊综合评价法、灰色综合评价法、TOPSIS法、人工神经网络等[1～6]，这些方法产生于特定的背景，有着各自的适应性，丰富了评标决策方法的理论与实践研究[7]，但存在的问题也非常明显，缺乏系统评价的最优标准，且评价方法过于简单，缺乏科学性。在这些研究中，值得关注的是，将单一的数学模型以及这些模型改进后的方法引入评标过程中的研究十分普遍，而综合两种及两种以上数学模型的评标决策研究为数不多[8]。针对现有评标方法的缺陷与不足，本文从评标影响因素的组成，评标方法的选取以及指标因素权重的确定进行分析与探讨，结合模糊物元模型与综合集成赋权方法的优点，将组合方法引入评标决策过程中，试图为评标决策的过程提供一种更为科学有效的方法。

1 建立合理的工程评标指标体系

建筑工程项目的评标决策是一个严谨且复杂的过程[9]，在评标决策时，无论选用何种评标模型，均需要建立一定的评标决策因素集与其相应的子因素集，这是招标文件与评标工作的关键与基础，是评标决策过程的第一步。针对工程项目的特殊性，评标标准的建立必须经过细致的分析与理解，综合考虑各方面影响因素，从而建立系统的评价指标体系。综合评价指标体系的构建具体要满足“优度”的标准[10]，主要包括评价指标因素的必要度、相互独立性、稳定度与协调度等方面。在实际的评标过程中，影响评标的因素很多，具体的指标分类方法也有很多种[11]，在此，结合工程评标实际以及指标体系建立的标准，本文在阅读大量文献的基础上，综合前人的研究成果，将工程评标的主要指标分为经济标、技术标、商务标三个一级指标, 每个一级指标下又分成若干个二级指标，从而建立一个合理的、多层次、多维度的评标指标体系[12]，如图1所示。

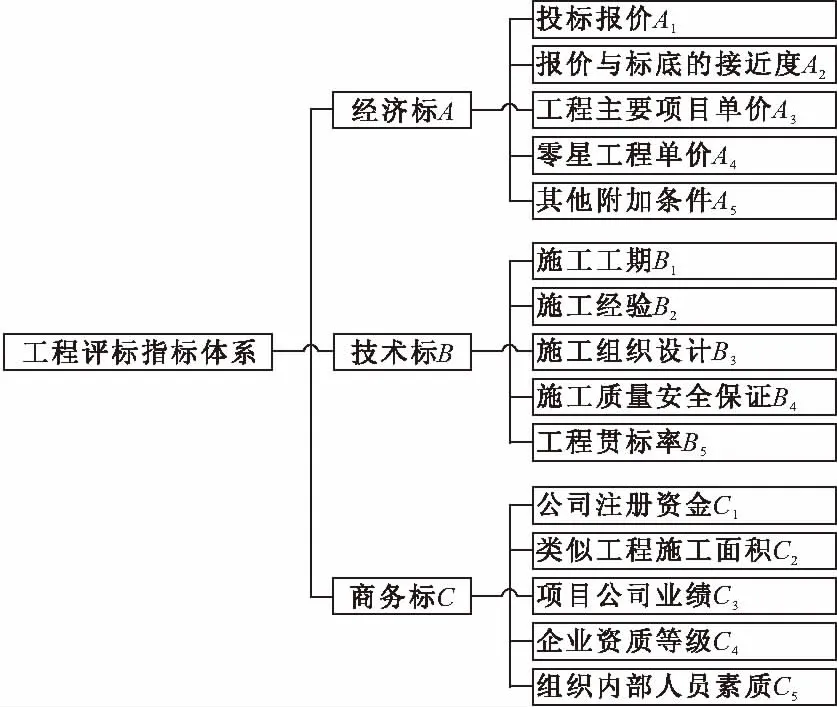
图1 工程项目评标指标体系

投标文件一般包括经济标、技术标和商务标三大块，经济标主要指与工程量清单相对应的投标报价，技术标主要包括施工组织设计的技术实力与经验，商务标是投标公司证明其有资质投标和中标后有能力履约的条件。其中，在这些指标中，商务标是企业参与投标的准入条件，经济标决定了企业能否入围，技术标则是投标中的最后一环。在图1的二级指标中，对于具体的定量指标，直接带入实际数据即可，而对于抽象的定性指标，则根据专家打分等方式进行定量化处理。

2 评标模型的构建

2.1 确定从优隶属度

从优隶属度是指各单项评价指标相应的模糊量值, 从属于标准方案各对应评价指标相应的模糊量值隶属程度。假设在工程项目招投标过程中，有m个投标单位和n个评价指标，由于各指标特征值对于量化结果来说，评价原则不同，对于不同的隶属uij度的计算过程如下：

越大越优的正指标：

uij=(xij-minxij)/(maxxij-minxij)

(1)

越小越优的负指标：

uij=(maxxij-xij)/(maxxij-minxij)

(2)

式中，xij为评标体系中的指标实际值，maxxij，minxij分别为投标单位的第j项指标对应的所有量值xij中的最大值，最小值。

2.2 构造评标物元模型

在物元分析中所描述的事物M及其特征C和量值x三要素构成物元R=(M,C,x)。如果量值x具有模糊性，便称其为模糊物元。对由m个投标单位，n个评价指标与其相对应的量值所构成的复合模糊物元Rmn记为：

式中，Mi为第i(i=1,2,…,m)个投标单位，Cj为评标体系中的第j(j=1,2,…,n)项指标，uij为第i个投标单位第j项指标所对应的模糊量值，uij由(1)(2)式确定。

2.3 最优模糊物元与关联系数复合模糊物元

最优模糊物元R0n是由从优隶属度模糊物元Rmn中量化指标的从优隶属度的最大值确定的，因此，R0n中各指标的从优隶属度均为1。

由灰色系统中的关联度的定义，对于第j项指标，第i个投标单位与最优投标单位的关联系数Yij可以表示为：

Yij=(Δmin+ρΔmax)/(Δij+ρΔmax)，

Δij=|u0j-uij|=|1-uij|。

式中，Δij为第i个投标单位与最优投标单位的第j项指标量值之间的绝对差，Δmax，Δmin分别为Δij的最大值与最小值。ρ为分辨系数，通常取ρ=0.5。

由以上的分析可以建立关联系数复合物元模型：

2.4 Delphi-AHP法与熵值法进行综合集成赋权

量化指标综合权重的确定将会对量化的结果产生很大影响，因此指标权重是否科学、合理是保证指标结构与功能统一的关键。本文将AHP得到的主观权重αj与熵值法确定的客观权重βj进行综合集成，得到综合集成权重ωj：

ωj=pαj+(1-p)βj，j=1,2,…,n

式中，p为主客观权重的偏好系数，p∈[0,1]，由文献[13]的分析，主观权重应该是求取指标权重系数的基础，因此，此处结合本文的评标指标体系，取p=0.6较为合适。

2.5 综合关联度复合物元与综合排序

由确定的综合集成权重ωj以及关联系数Yij，得到工程评标单位的综合关联度复合物元：

式中，Hi为第i个投标单位的灰色关联度(i=1,2,…,m)，Hi越大，表示该投标单位的实力越强。由此可以得出各投标单位的综合排序。

3 应用实例

某建筑工程采用工程量清单计价模式并公开招标，共有5家投标单位，案例选取图1中的投标报价、工程主要单价、施工工期、施工组织设计、施工质量安全保证、工程贯标率、公司注册资金、类似工程施工面积等8项指标组成评标体系，各单位的相关原始评标数据如表1所示。

表1 投标单位相关指标原始数据

由步骤2.1最优隶属度公式计算评价指标的模糊量值，并由步骤2.2求得5家评标单位的8维模糊复合物元R为：

由步骤2.3得到最优模糊物元R0与关联系数复合物元模型RY分别为：

由步骤2.4计算各指标AHP权αj、熵权βj、以及综合集成权重ωj分别为：

αj=(0.285,0.099,0.134,0.122,0.058,0.112,0.125,0.065)T

βj=(0.043,0.054,0.194,0.086,0.097,0.032,0.344,0.150)T

ωj=(0.188,0.081,0.158,0.108,.074,0.085,0.212,0.094)T

由步骤2.5确定该工程的5个投标单位的综合关联度复合物元RH为

通过比较关联度的大小，由H4>H3>H1>H2>H5，可以判定D为最佳投标单位，从而可以将工程项目发包给投标单位D。

4 结 语

综合工程评标决策体系的建立有利于评标的科学性，基于模糊物元-综合集成赋权的评标模型结合了物元模型、AHP赋权与熵值法的优势，以定量的数值表示判断结果，可以更直观的评价投标方案，衡量投标单位的实力状况，有助于规范工程交易市场的秩序，促进公平竞争氛围的形成。此外，该模型可以采用软件编程实现，使评标人易于在短时间内合理地做出准确的判断，可操作性较强，可以广泛推广于其他领域方案的评定过程中。

[1] 樊胜军．层次分析法在建设工程评标中的应用[D].西安：西安建筑科技大学，2003．

[2] 高红江，刘 旭．基于模糊熵权的工程项目综合评标法[J]．建筑管理现代化，2009，23(2)：131-134．

[3] 吴耀兴，陈政辉．模糊综合评价法在工程项目评标中的运用[J]．建筑经济，2009，(10)：64-67．

[4] 刘 晴，王建平，王丛莹．基于灰色关联理论的建设工程评标方法研究[J]．工程管理学报，2010，24(2)：152-155．

[5] 徐志舜，刘振奎．基于TOPSIS法评标方法探讨[J]．价值工程，2012，(33)：107-108．

[6] 刘亮晴．基于人工神经网络的施工招标评标系统研究[D]．重庆：重庆大学，2006．

[7] 粟增德．基于含偏好约束锥的数据包络分析评标模型及其应用研究[D]．重庆：重庆大学，2006．

[8] 曹琳剑，刘炳胜，王雪青，等．DEA 和信息熵改进的评标方法研究[J]．重庆大学学报(社会科学版)，2011，17(2)：86-87．

[9] 夏恩君，苏广领．工程项目评标优化决策模型研究[J]．中国软科学，2003，(10)：133-134．

[10]李远远，云 俊．综合评价指标体系构建“优度”评价研究[J]．武汉理工大学学报(信息与管理工程版)，2010，32(1)：122-125．

[11]Mohamed M, Ahmed E-D, Moheeb E-S. New safety assessment model for civil engineering structure [J]. Journal of Professional Issues in Engineering Education and Practice, 2008, 134 (3): 315- 326.

[12]许远明，陶书金，曾令德．基于熵权—TOPSIS方法的施工评标模型应用研究[J]．工程管理学报，2012，26(5)：63-64．

[13]王明涛．多指标综合评价中权系数的一种综合分析方法[J]．系统工程，1999，17(2)：56-61．