关于高等代数教学中若干问题几何意义的探索

黄娟霞，张 静，王 飞

(陇南师范高等专科学校 数学系，甘肃 成县 742500)

高等代数是高等院校数学专业的一门重要的基础课程，其中的相关概念、判定定理繁多，且比较抽象，往往难以理解和把握，尤其对于初学者来说，学习这部分内容往往抓不住要领．然而，如果教师能够在教学时深入挖掘其几何意义，紧密使用数形结合的思想方法可以使复杂问题简单化、抽象问题具体化；能够将抽象的数学语言变为直观可视化的几何图形、抽象思维变为形象思维，这将有助于学生对高等代数问题本质的把握．因此，在高等代数的教学过程中，一定要注重对相关知识的几何意义深入挖掘，借助于几何的直观性，探索其几何意义，从而达到对代数问题本质的理解，这样可以达到事半功倍，化难为易的目的.

1 向量组线性相关概念几何意义的教学探索

向量组的线性相关概念是高等代数的一个重要概念，是高等代数课程后续学习内容的基础，但是它比较抽象，初学的学生如果掌握不好，很难学懂后续高等代数的相关内容，进而会大大削减学生学习高等数学的信心和兴趣．如何让学生直观、清晰地了解向量组线性相关概念蕴含的真正内涵呢？教学时教师可以从几何意义出发，善于利用矢量图形，在矢量图形中将要表达的代数意义刻划出来，这样学生可以直观地理解单个向量、两个向量，乃至多个向量线性相关的内涵，一般容易掌握．

定义1 如果向量组α1，α2，…，αs(s>2)中有一个向量可以用其他的向量线性表出，那么向量组α1，α2，…，αs称为线性相关的．由向量组线性相关的定义可以得到其几何意义：

结论1 对于单个向量α来说，如果α线性相关，则α=0.

结论2 对于两个向量α，β来说，如果α，β线性相关，则α，β共线，即一个向量可以由另一个向量线性表出，不妨设β=kα(如图1)．

结论3 对于三个向量α，β，γ来说，如果α，β，γ线性相关，则α，β，γ共面，即至少有一个向量可以由另外两个向量线性表出，不妨设γ=k1α+k2β(如图2).

图1 两向量共线 图2 三向量共面

结论4 对于一组n维向量α1，α2，…，αn来说，如果α1，α2，…，αn线性相关，则α1，α2，…，αn这n个向量同在某一个n-1维的“超平面”上，即至少有一个向量可以由其余n-1个向量线性表出．

2 欧氏空间中正交变换几何意义的教学探索

正交变换是欧氏空间中两种重要变换(正交变换和线性变换)中的一种，深入地理解它可以解决许多实际问题．在教学中广大教师往往都是将其与线性变换类比讲解，虽然理论上比较清晰，但可视化不强，因此，有必要从其几何意义入手进行分析，这样学生更容易理解和接受．

定义2 欧氏空间V的线性变换A称为正交变换，如果它保持任意两个向量的内积不变，即对任意α，β∈V，有(Aα，Aβ)=(α，β).

由正交变换的定义，对任意α∈V，有(Aα，Aα)=(α，α)，即|Aα|=|α|，亦即正交变换不改变向量的长度.设正交变换A在任一组标准正交基下的矩阵是正交矩阵A，在几何上，当|A|=1时，正交变换表示把向量α旋转某一角度θ；当|A|=-1时，正交变换表示把α关于坐标轴做镜面反射再旋转某一角度θ(如图3).

图3 正交变换

3 线性方程组的通解与其导出组的通解之间关系几何意义的教学探索

一般线性方程组通解的求法是高等代数教学中的一个重要知识内容，它的通解应该为它的导出组的通解与其本身的一个特解组成，然而现行教材中仅是从该问题的代数理论层面进行讲解，相对抽象，学生不易接受，如果能将此问题结合其几何意义进行深入分析，则会起到事半功倍的效果.

在几何上，取空间坐标系[Ο，x，y，z]，如图4所示．

图4 三元线性方程组的通解

4 Cramer法则几何意义的教学探索

在高等代数中，利用加减消元法得到2×2、3×3线性方程组的公式解，通过引入二阶、三阶行列式对这些公式解进行简洁地表示，从而得到2×2、3×3线性方程组的Cramer法则.但当未知量的元数继续增多时，难以再用加减消元法求解线性方程组，转而研究二阶、三阶行列式的结构，找出它们共同的规律，根据这些规律来定义n阶行列式，然后用它来表示n×n线性方程组的解，即n×n线性方程组的Cramer法则.下面应用分块矩阵和向量代数的数量积直接推导出3×3线性方程组的Cramer法则，并用平行六面体的体积解释了3×3线性方程组的Cramer法则，进而将这一几何解释推广到n×n线性方程组的Cramer法则．

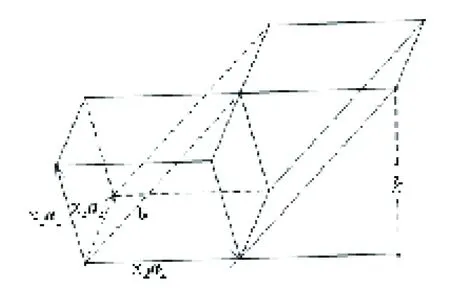
图5 3x3线性方程组的Cramer法则

这样利用平行六面体的体积解释了3×3线性方程组的Cramer法则.类似地，可以用维的“平行六面体”的“体积”来解释n×n线性方程组的Cramer法则.

5 结束语

对向量组线性相关概念、欧氏空间的正交变换、一般线性方程组的通解与其导出组的通解的关系以及Cramer法则等相关知识进行几何意义的探讨，不仅可以使学生很好的学习到高等代数知识，有效培养学生的思维，同时也可以使学生掌握这样一种学习大学数学的通用方法，对他们以后的学习受益匪浅，对于高等代数这门比较艰涩的抽象理论课程，其教学方法是值得我们数学工作者进一步研究的一个很好课题．

参考文献：

[1]北京大学数学系.高等代数[M].北京:高等教育出版社，2003.

[2]吕林根，许子道.解析几何[M].北京:高等教育出版社，1998.

[3]黎伯堂，刘桂真.高等代数解题技巧与方法[M].山东:山东科学技术出版社，2003.

[4]李成杰.关于高等代数教学的思考与探索[J].高等数学研究，2010，13(2):47-48.