一类四阶非线性微分方程边值问题解的存在性探究
成连连,郭红梅
(1.山西体育职业学院,山西 太原 030006;2.山西生物应用职业技术学院)
一类四阶非线性微分方程边值问题,在其用于描述两端简单支撑的弹性梁、弯曲弹性梁的形变及平衡状态的非共振等力学问题的研究中,具有相当独特的作用和极为重要的地位.由此背景,其解的存在性也得到广泛的关注和研究.
下面考察四阶边值问题
(1)
解的存在性.其中f∈C([0,1]×R2,R) ,定义f:[0,1]×R2→R是连续的,且存在两个正实数λ1,λ2,0≤λ1+λ2≤2 ,使得对∀t∈[0,1],u1≥u2,v1≥v2有
f(t,u1,v1)-f(t,u2,v2)≥
-λ1(u1-u2)-λ2(v1-v2)
(2)
本文是在f同时含有u′ 和u″ 项的情况下,利用上下解方法探究四阶边值问题解的存在性[1].
1 预备知识
定义1 如果x(t)∈C4[0,1]满足
则称x(t)为(1)式的下解.如果y(t)∈C4[0,1]满足
则称y(t)为(1)式的上解[2].
引理1 若(E,K)是序Banach空间, [a,b]⊂E,T:[a,b]→E是单调增的紧映射,并且a≤Ta,Tb≤b,那么T在[a,b]内有不动点.
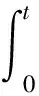
2 主要研究结果及证明

K={x∈C[0,1]|x(t)≥0,0≤t≤1} ,
定义“≤”:∀x,y∈E,y≤x⟺x-y∈K,(E,K)在E中的半序关系是有序的Banach空间.
定理1 若(1)有下解x和上解y,使得∀t∈[0,1],x″(t)≤y″(t) ,则存在u∈C4[0,1]是(1)的解,并且u满足对
∀t∈[0,1],x″(t)≤u″(t)≤y″(t)成立.
证明 令w(t)=u″(t),那么(1)等价于
(3)
令D={w∈E|w″∈E,w(0)=w(1)=0},显然D⊂E.
令L:D→E.N:E→E如下:


由L和N的定义可知,问题(1)等价于
Lw=Nw
(4)
如下证明(4)是可解的.
步骤1 证明L:D→E是可逆的[2].
设η∈E,由Lw=η,则
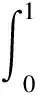

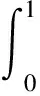
步骤2 证明l-1:E→E是连续的[3].
设η∈E.{ηn}⊂E,ηn→η.令L-1η=w,L-1ηn=wn,则
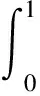
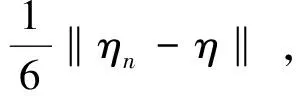
步骤3 证明L-1:E→E是紧的.
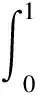
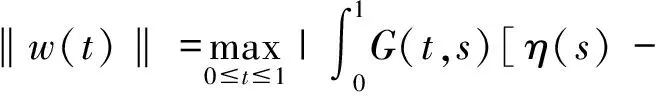
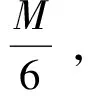
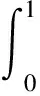
所以L-1(X)是等度连续的,根据Arzelz-Ascoli定理可知,L-1:E→E是紧的.
步骤4 证明L-1N:E→E是增的[3].
假设η1,η2∈E,η1≤η2,由(2)式我们可以得出,Nη1≤Nη2.令w1=L-1Nη1,w2=L-1Nη2,那么Lw1≤Nη1≤Nη2≤Lw2,由引理2可得:w1≤w2,即L-1N:E→E是增的.
步骤5 证明若α=xn,β=yn,那么α≤L-1Nα,L-1Nβ≤β.
由x是下解和L,N的定义,我们可知

(5)
令α1=L-1Nα,即Lα1=Nα,则有
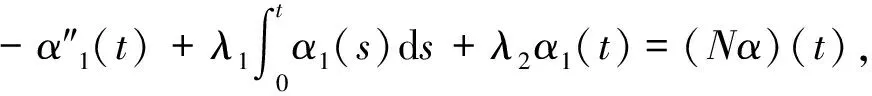
(6)
令P(t)=α(t)-α1(t) ,由(5)、(6)两式可得到

由引理2可以得到,P(t)≤0,α≤α1, 即α≤L-1Nα,同理可得L-1Nβ≤β.
由引理1知,L-1N在[α,β]内存在不动点w且有α≤w≤β.由(3)和(4)式可知定理的结论成立.

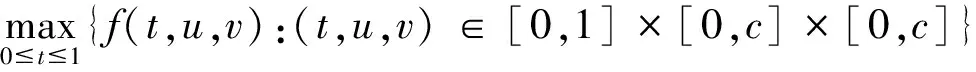
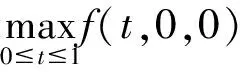
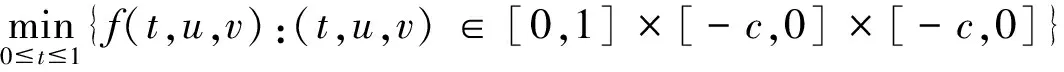
证明 在①中令x(t)≡0 ;y(t)=c(6t2-t4)在②中令x(t)=-c(6t2-t4),y(t)≡0.
容易验证,x,y分别是(1)式的下解和上解.故由定理可知,在①情况下(1)式存在正解,在② 情况下(1)式存在负解.
依据以上结论,我们可以断定下面问题
(7)

参考文献:
[1]熊骏.二阶微分方程边值问题解的存在唯一性讨论[J].长江大学学报,2006(9).
[2]北京师范大学.常微分方程[M].北京:高等教育出版社,2001.
[3]王信峰,吴静.一个增算子不动点定理及其在Banach空间非线性方程的应用[J].应用泛函分析学报,2005(1).
[4]栾世霞,孙钦福,颜伟.Banach空间非单调算子方程新的不动点定理[J].曲阜师范大学学报,2008(1).
[5]王彩华.一类二阶常微分方程组边值问题正解的存在性[J].赤峰学院学报,2010(3).

