风廓线雷达极低信噪比信号的小波方法提取

荔千妮, 吴 蕾

(1.成都信息工程学院,四川成都610225;2.中国气象局气象探测中心,北京100081)

0 引言

随着风廓线雷达在气象领域的迅速发展,国内外的许多学者对风廓线雷达的信号处理方法做了深入研究,希望能够获得更加精确的风廓线雷达基数据,以提高风廓线雷达的探测能力。比如国外的Hopper研究了各种窗函数对WFFT的影响,得出Hanning窗处理的谱泄漏低于Hamming窗和矩形窗的结论;Wilfong等[2]提出的用Blackman-Harris滤波器取代相干积累的方法,这种方法降低了因相干积累带来的频谱混叠效应;Boyer等[3]分析了复倒谱、参数建模谱估计算法和MUSIC算法在提取风谱中的应用效果,发现MUSIC算法有较高的谱分辨率,同时还指出,因为MUSIC算法完成的只是对风谱的检测,风速等参量的估计需另做处理,而且MUSIC算法的计算量很大,硬件实现困难。国内,胡明宝等[4]提出的最大熵法在风廓线雷达信号应用,并得出在信号强度较弱的情况下最大熵法分析效果优于FFT方法;而且最大熵法获得的频谱比较光滑,表明最大熵法对随机噪声也有一定的抑制作用。但是最大熵法的缺点是滤波器阶数对谱的分辨率影响较大不易确定。不论是国际还是国内,提出的以上新算法、新方案都会由于某种原因而不能被实际采用,目前的风廓线雷达信号处理方法仍采用基于FFT的经典信号处理方法。

然而基于FFT的经典风廓线雷达信号处理方法也存在一定的局限性,它只适用于回波信号所含噪声比较单一的情况,比如雷达机本身的噪声和大气背景噪声。但是实时的风廓线雷达回波信号的频率成分非常复杂,而且干扰信号具有很强的随机性。当存在频率较接近有用信号频率的强干扰信号时,单用FFT方法已经不能对有用信号进行提取,这时的频率函数不再是高斯分布的形式,频谱会出现多峰的情况,这样就很难对谱矩做出正确的判断。造成这种情况的主要原因在于傅里叶变换无法将时域和频域两种视角结合起来,当数据从时域转换到频域后就丢失了时间信息,用于非平稳随机信号时就会遇到困难。

由于傅里叶变换存在这种局限性,在风廓线雷达信号处理中开始引入小波分析的方法。小波分析属于时-频分析,在非平稳随机信号的处理中小波分析具有突出优势。小波变换的时频域多尺度化分析方法的特点,更适用于回波信号中夹杂瞬态杂波的情况。小波分析具有多分辨率分析的特点,在时域和频域都具有表征信号局部特性的能力。

1 小波滤波方法分析

小波分析作为信号处理领域一个重要的方法,具有独特的优势。目前小波滤波的方法大致分为3种。即模极大值重构滤波算法、小波阈值滤波算法和空域相关滤波算法。3种方法都有其各自的优势和劣势,哪种方法也不完全优于其他方法,表1给出3种方法的定性比较结果。结合阈值去噪和空域相关滤波方法的优缺点提出改进的空域相关算法使其达到对风廓线弱信号提取的有效结果。

表1 3种小波方法的定性比较

在小波分析中,噪声与雷达回波的Lipschitz指数表现出截然相反的尺度特性,在小波域,信号的小波系数随着分解尺度的增大而增大,噪声的小波系数随尺度的增大而迅速减小(见图1)。所以适当的设定阈值,就可消除全部噪声,同时又很好地保留细节信息。由于风廓线雷达回波信号非常微弱,随着分解尺度的减小,噪声系数的幅度迅速增大,要想在小尺上仅靠设定阈值达到消除噪声并保留细节信息是不可能的。阈值去噪要掌握信号的先验信息,如何进行阈值估计直接影响去噪效果和信号质量。阈值设定较大有可能在去除噪声的同时也去除了部分细节信息,阈值设定较小虽然可以保留部分细节信息但也保留了一部分噪声。所以能否在小尺度上对噪声和信号的进行分离是小波阈值方法改进的一个方向。

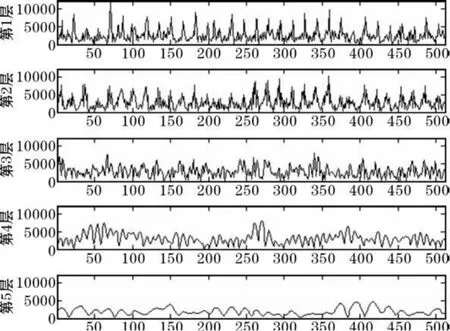
图1 五尺度小波分解的各尺度高频系数

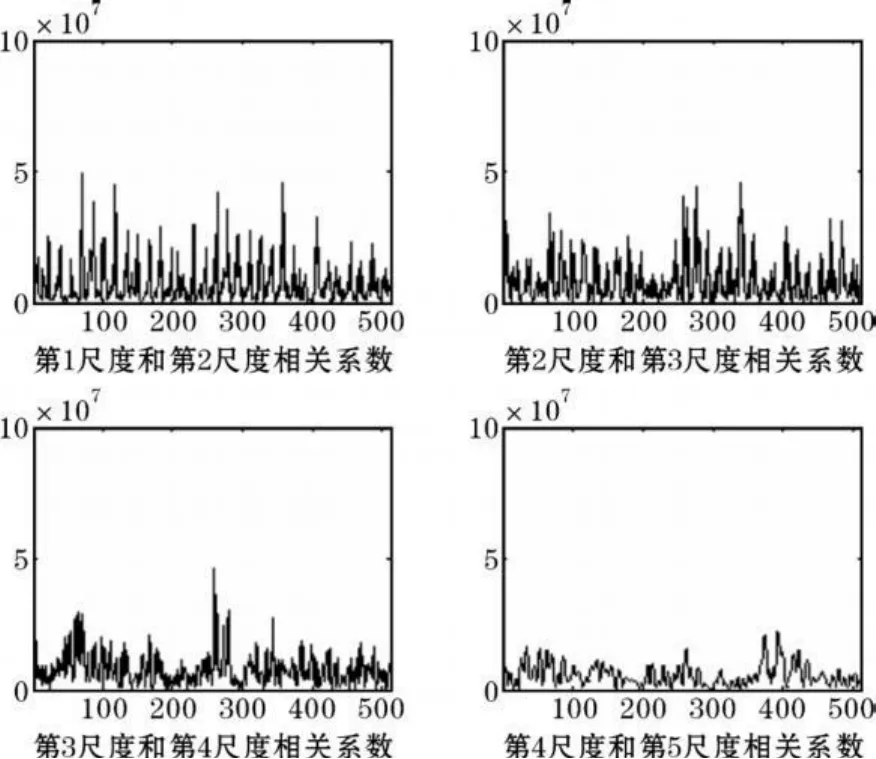
图2 单一周期相邻尺度相关系数

空域相关滤波是根据信号的小波系数比噪声的小波系数在各尺度上具有更加明显的相关特性而提出的。空域相关滤波方法通过相邻尺度上对应点处的相关性确定该位置的小波系数是信号系数还是噪声系数,并对其进行筛选,去除噪声系数,保留信号系数。经此处理后的小波系数基本上保留了信号的边缘信息,达到了去除噪声的目的。以下是关于空域相关算法的定义:

相邻尺度的相关系数定义为:

其中 Wf(j,k)表示尺度j,位置k处含噪信号的小波变换。Corrj(k,τj,k)表示尺度j点K处的相关系数。τj,k满足

(2)式表明τj,k可使相邻尺度上的小波系数的相关性最强。

对相关系数作归一化处理,使尺度相关系数和小波系数具有可比性:

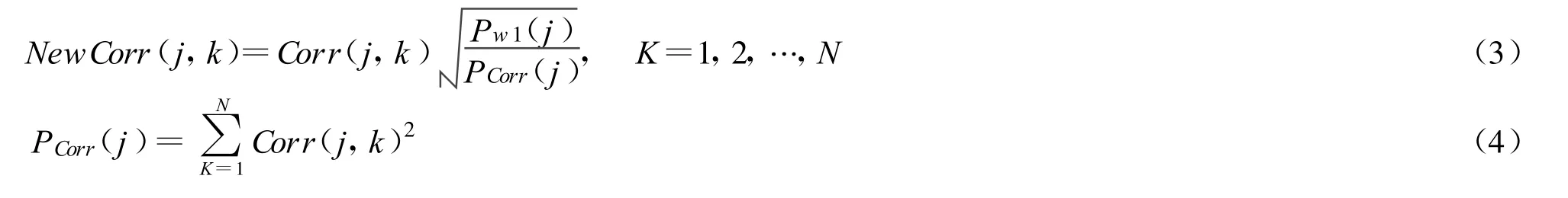
图2是用空域相关算法对风廓线雷达信号的小波系数相关处理结果图。从图中可以看出在小尺度上,信号的相关性非常明显,很容易辨别信号的细节信息;在大尺度上的相关系数也基本滤除噪声。但是在处理风廓线雷达信号时,小波空域相关算法仍存在以下缺点:

τj,k值确定困难。空域相关算法的重点在于如何对τj,k值进行确定,当信号极其微弱时,在小尺度上用(2)式不能得到正确的 τj,k值。因此,需要寻找一种在低信噪比情况下同样能准确确定τj,k值的方法。

不适用于极低信噪比情况下的信号去噪。空域相关算法中的相关系数实际上还是用于计算阈值,属于阈值去噪的一种改进方法。所以在信噪比极低的情况下阈值去噪会过多保留由噪声引起的奇异点,从而使重构信号出现很多“毛刺”现象(见图3)。因此,需要在小尺度上找到一种新的降噪方法消除这种毛刺现象。

2 对空域相关方法的改进

结合风廓线雷达信号极低信噪比的特点以及现有空域相关算法的优缺点,对现有空域相关算法做了以下改进。

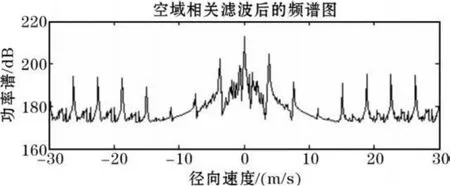
图3 原有空域相关算法产生的频谱图

2.1 τj,k值的确定

针对信号信噪比极低时,τj,k值难以确定的缺点。根据风廓线雷达信号的严格周期性和噪声的不相关性。对算法做出改进,即对需要做谱平均的 N组数据,假设N=4,一个功率谱的4个雷达脉冲信号为p1(n),p2(n),p3(n)和p4(n)的小波高频系数在相同尺度,相同位置处进行相关运算。

设风廓线雷达的相邻两个连续回波信号所包含的噪声不具相关性,且与信号不相关。由式(1)和式(2)得

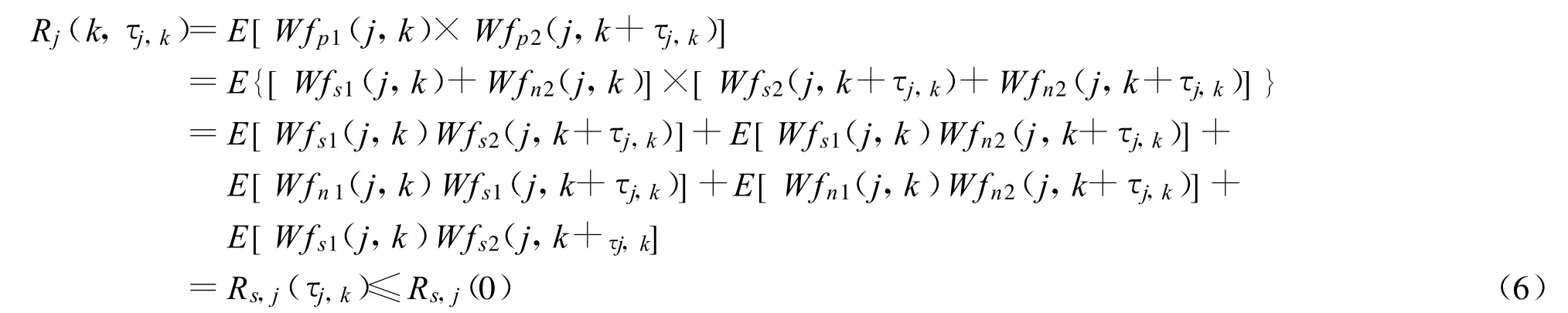
式中 Wfp1(j,k)和 Wfp2(j,k)分别为p1(n)和p2(n)在尺度j,和位置k处的小波系数。由式(6)看出相邻两个雷达回波信号在小波分解相同尺度上的相关运算在τj,k=0时,取得最大值。相同尺度的相关系数定义为

图4是对相邻两个回波信号在相同尺度上做的相关处理结果。比较图2和图4可以看出,相邻两个回波信号的小波系数在相同尺度相同位置上的相关性比一个回波信号的小波系数在相邻尺度上相同位置的相关性更强,所以,对两个相邻的回波信号在相同尺度,相同位置进行相关运算,能够更好地提取信号细节并抑制噪声。

2.2 极低信噪比信号在小尺度上的降噪方法

对阈值去噪的分析可知,在小尺度上难以对极低信噪比的风廓线雷达回波信号做阈值去噪处理,为此,在小尺度上采用归一化相关系数代替含噪声信号的小波系数。改进算法采用(8)式所示

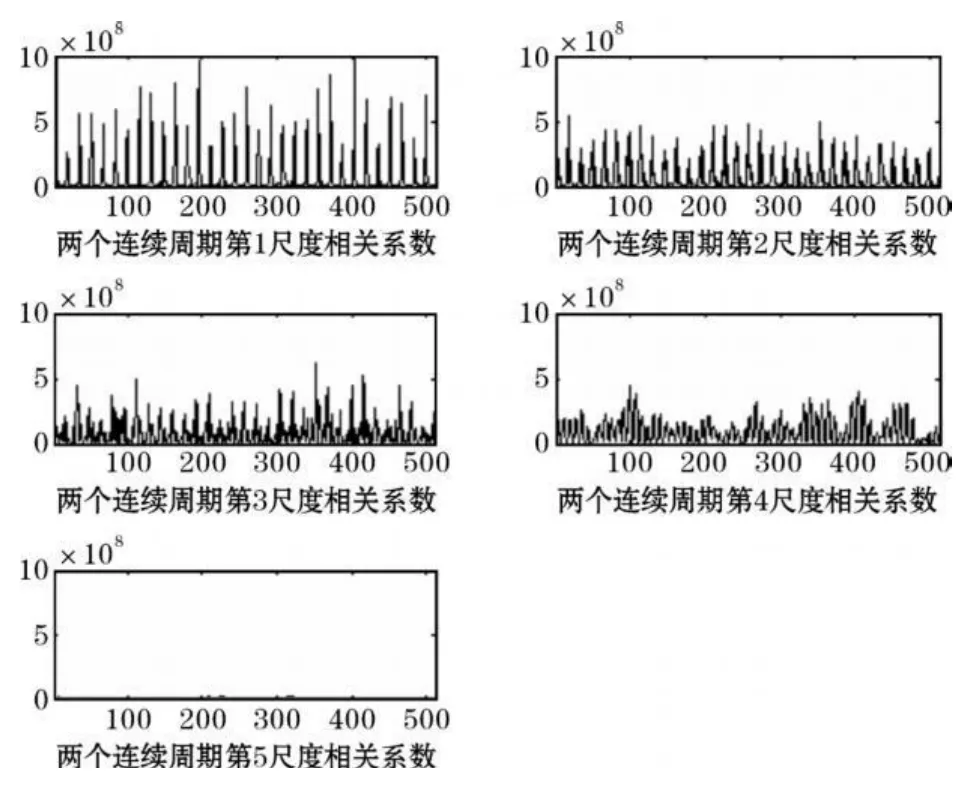
图4 两个连续周期相同尺度的相关系数

结合(3)～(5)式可得,

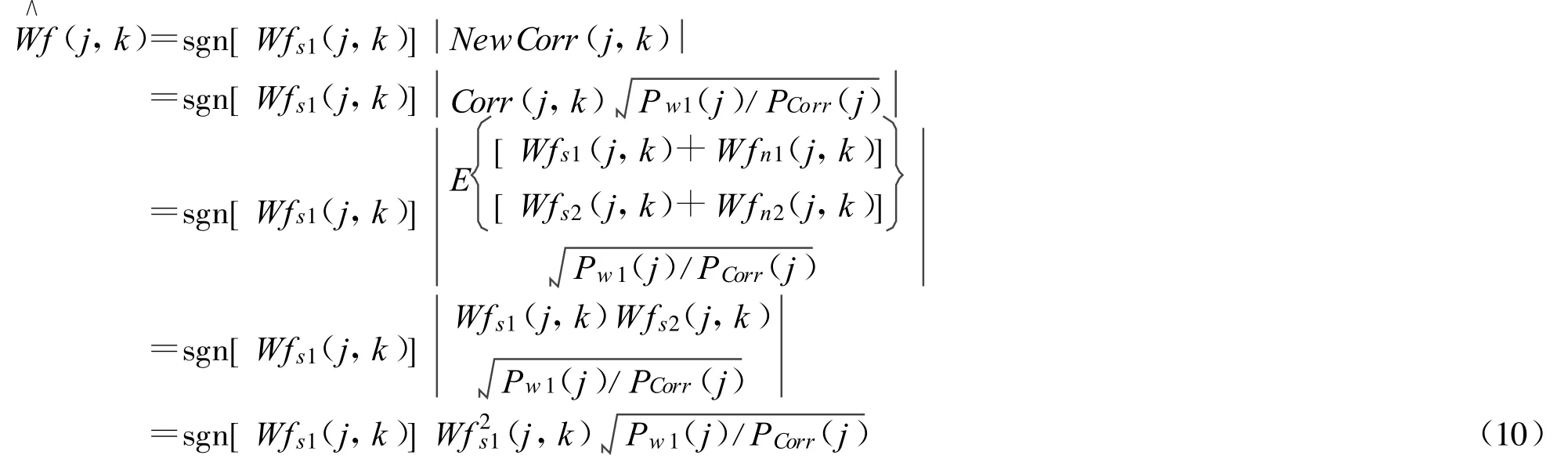
通过上式的推导过程可知,由(8)式确定的小波系数小尺度上不仅表现出较强的抑制噪声作用,同时还增大了回波信号的强度。

2.3 改进空域相关滤波算法的实现

根据以上对空域相关算法的改进,得出基于改进小波空域相关滤波的风廓线雷达极低信噪比信号降噪算法的实现流程,如图5所示。

该流程是对需要做谱平均的两个相邻回波信号p1(n)和p2(n)的处理,对于谱平均数为4的回波信号,还需进行p2(n)和p3(n),p3(n)和p4(n)的相关滤波处理。然后对其进行谱平均就得到一个功率谱数据。

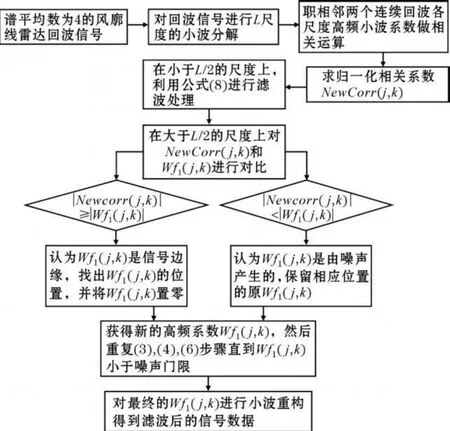
图5 程序流程图

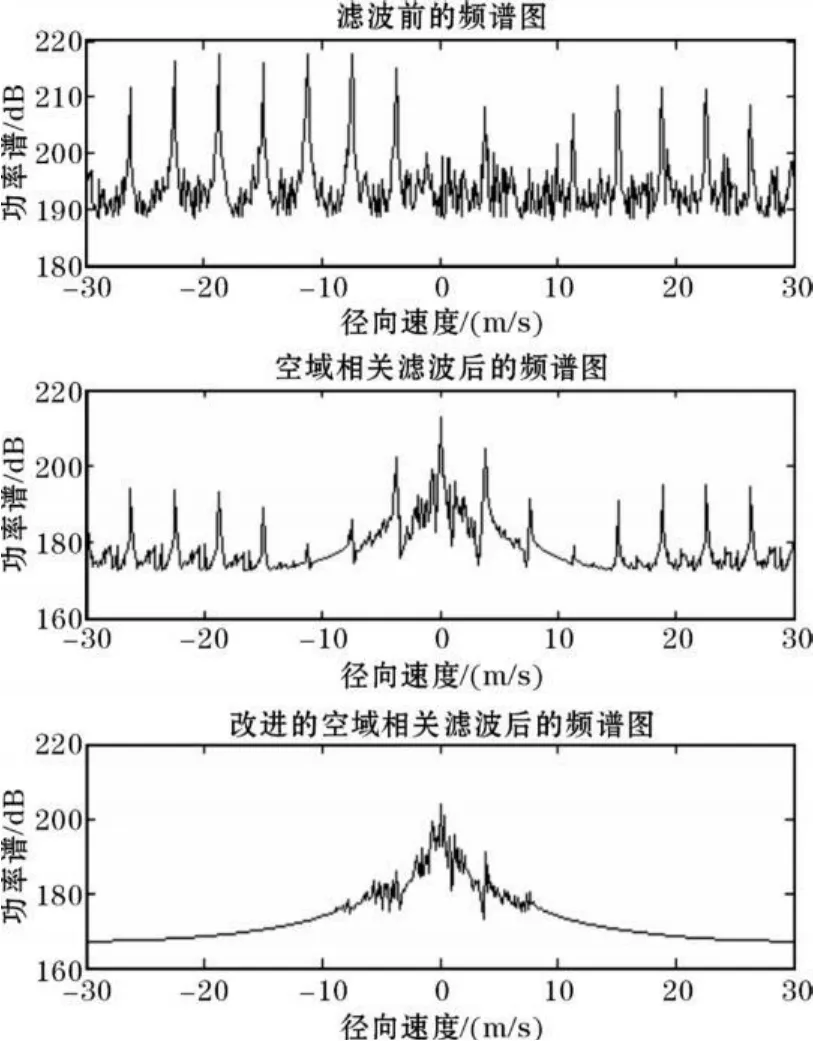
图6 处理地模式IQ数据产生的一个距离库功率谱数据对比

3 实验结果分析

实验中使用风廓线雷达回波信号是谱平均数为4,时域累计数为100,重复周期为306,FFT点数为512的边界层风廓线雷达低模式和高模式数据。

由图6的对比可以看出,改进后的空域相关滤波算法与原空域相关算法相比,首先它消除了原有方法产生毛刺的现象,其次改进后的空域相关算法产生的功率谱的谱峰更加凸显。

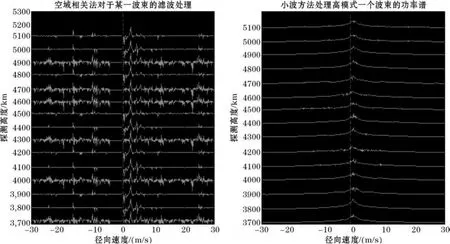
图7 改进空域相关滤波处理高模式IQ数据产生的一个波束功率谱数据对比

图7是利用改进方法对一个波束高模式IQ数据处理结果与经典FFT信号处理方法的对比。由于风廓线雷达高模式的高层距离库的回波信号几乎全部被噪声淹没,其信噪比非常低。由第一部分内容可知空域相关算法不适用于低信噪比信号的滤波处理。但是实验中选择最高层的15个距离库的极低信噪比回波数据,对其进行处理得到结果与经典方法对比消噪效果非常明显。

4 结束语

风廓线雷达回波信号不但非常微弱,而且随着探测高度的增加雷达反射率迅速减小。风廓线雷达对信号的提取能力直接影响风廓线雷达本身的探测能力,以及生成产品的可靠性。提高风廓线雷达对信号的提取能力对风廓线雷达的应用发展显得尤为重要。所以针对现有风廓线雷达信号处理方法的缺点与局限性,结合小波滤波的时频局部化分析的特点对现有空域相关算法进行改进。实验结果表明该算法可适用于极低信噪比的情况,能够消除原有空域相关算法产生的毛刺现象,在保留信号的细节信息同时可以大幅度提高信号的信噪比。

[1] Hooper D A,Signal and Noise Level Estimation for Narrow Spectral Width Returns Observed by the Indian MST Radar[J].Radio Sience,1999,34(4):859-870.

[2] Wilfong T L,Merritt D A,Lataitis R J,et al.Optimal Generation of Radar Wind Profiler Spectra[J].Atmos O-ceanic Technol.1999,16(6):723-733.

[3] Boyer E,Petitdidier M,Comeil W,et al.Application of Model-based Spectral Analysis to Wind-profiler Radar Observations[J].Annales Geophysicae,2001,19(8):815-824.

[4] 胡明宝,郑国光,张培昌.最大熵法在风廓线雷达谱分析中的应用研究[J].光谱学光谱分析,2012,32(4):85-89.

[5] 李仲宁,罗志增.基于小波变换的空域相关法在肌电信号中的应用[J].电子学报,2007,35(7).

[6] 马晓岩,李广柱,张贤达,等.基于小波变换的雷达信噪比改善分析[J].清华大学学报(自然科学版),2003,43(3):422-424.

[7] 张海波,叶晓慧.一种改善微弱信号信噪比的小波变换消噪法[J].现代电子技术,2009,(4).

[8] 何平.相控阵风廓线雷达[M].北京:气象出版社,2006.

[9] 李翔,张久文.单脉冲雷达微弱信号检测方法研究[D].兰州:兰州大学,2010.

[10] 王莎,阮征,葛润生,等.风廓线雷达探测大气返回信号谱的仿真模拟[J].应用气象学报,2012,23(1):20-29.

[11] 曲巍崴,高峰.基于噪声方差估计的小波阈值降噪研究[J].机械工程学报,2010,2(46):28-33.

[12] 华春红,任章,张敏虎.基于自适应阈值估计的模极大值去噪方法[J].航天控制,2011,1(29):37-47.